在數據分析的世界裏, “距離” 不僅僅是地圖上兩點之間的路程。
距離 ,本質上是衡量兩個事物 “相似度” 的尺子。
- 距離越近 = 相似度越高
- 距離越遠 = 差異越大
如果你想做用户畫像聚類、想做商品推薦系統,或者想識別信用卡欺詐交易,你首先要選對這把“尺子”。
本文將帶你全面瞭解數據分析中常用的各種距離度量,從最直觀的歐氏距離到複雜的時間序列距離。
為了方便理解,我將它們分為了五大門派。
1. 第一門派:幾何空間的測量者
這一類距離最符合我們的直覺,通常用於處理數值型數據(比如身高、體重、經緯度)。
1.1. 歐氏距離:最直觀的“直線距離”
歐氏距離就是我們常説的 “直線距離”。
在二維平面上,兩點間的歐氏距離就是連接它們的直線長度。
應用場景:
- 外賣配送: 假設你是無人機送外賣,不受道路限制,直接飛過去,這就是歐氏距離。
- K-Means 聚類: 最常用的距離度量。
代碼示例:
import numpy as np
# 後面的代碼示例多次用到 distance,不再重複引用了
from scipy.spatial import distance
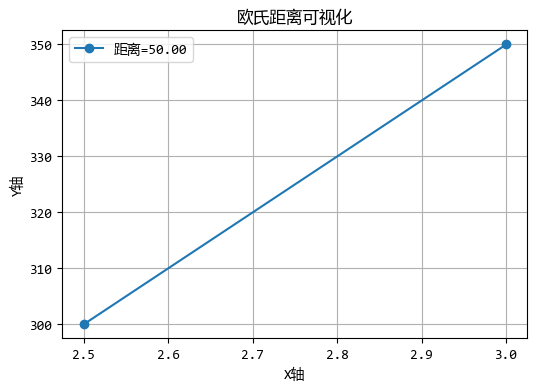
# 兩個用户的特徵:[活躍時長(小時), 消費金額(元)]
user_A = [2.5, 300]
user_B = [3.0, 350]
d_euclidean = distance.euclidean(user_A, user_B)
print(f"歐氏距離: {d_euclidean:.2f}")
# 運行結果:
'''
歐氏距離: 50.00
'''
圖形化效果如下:
注意:歐氏距離對數據的尺度敏感!如果特徵的單位不同(如年齡和收入),直接計算會導致收入特徵主導距離計算。
1.2. 曼哈頓距離:城市街區的走法
想象在紐約曼哈頓的街道上行走,你不能斜穿大樓,只能沿着街道走。曼哈頓距離就是這種 “城市街區距離”。
應用場景:
- 城市物流: 真實的快遞員配送路徑估算。
- 高維數據: 在某些高維數據中,曼哈頓距離比歐氏距離更能抗干擾(Robust)。
代碼示例:
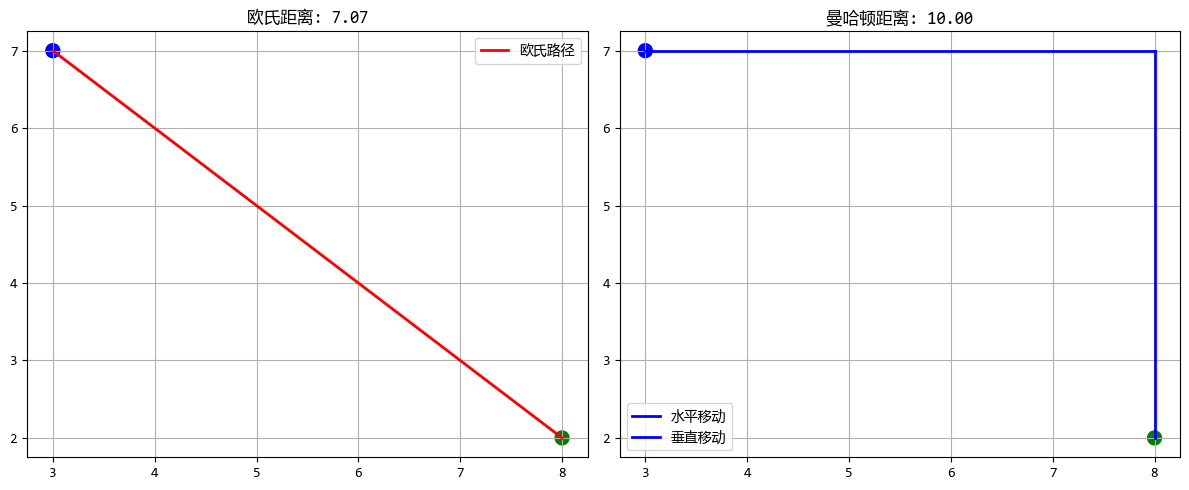
# 外賣配送示例:從餐廳到顧客的路徑
restaurant = np.array([3, 7]) # 座標(3,7)
customer = np.array([8, 2]) # 座標(8,2)
euclidean = distance.euclidean(restaurant, customer)
manhattan = distance.cityblock(restaurant, customer)
print(f"餐廳到顧客的直線距離(歐氏): {euclidean:.2f}")
print(f"餐廳到顧客的街區距離(曼哈頓): {manhattan:.2f}")
# 運行結果:
'''
餐廳到顧客的直線距離(歐氏): 7.07
餐廳到顧客的街區距離(曼哈頓): 10.00
'''
1.3. 切比雪夫距離:棋盤上的王者
也就是國際象棋中“國王”移動的步數。國王可以橫着走、豎着走,也能斜着走,且步數都算 1。
它只在乎數值差最大的那個維度。
應用場景:
- 倉儲物流: 龍門吊抓取貨物,橫向移動和縱向移動可以同時進行,時間取決於最遠的那個方向。
代碼示例:
d_chebyshev = distance.chebyshev(user_A, user_B)
print(f"切比雪夫距離: {d_chebyshev:.2f}")
1.4. 閔可夫斯基距離:距離的通用公式
它是上面三種距離的“爸爸”。通過一個參數 p 來控制:
- 當 p=1 時,就是曼哈頓距離。
- 當 p=2 時,就是歐氏距離。
- 當 p=∞ 時,就是切比雪夫距離。
應用場景: 當你不確定用哪種幾何距離時,可以調節 p 值來尋找最優解。
代碼示例:
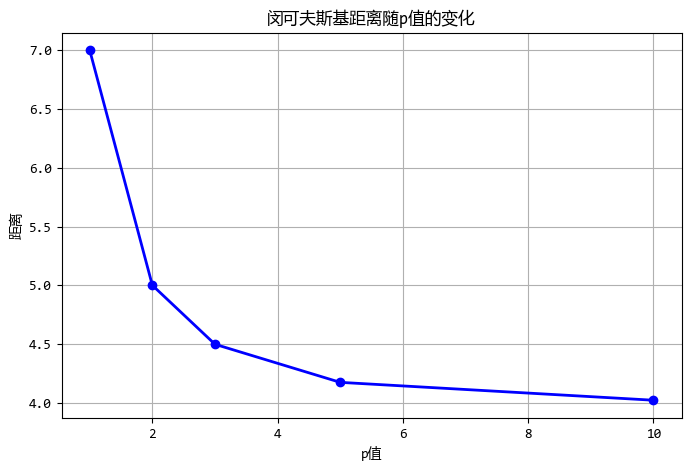
# 對比不同p值的效果
point1 = np.array([0, 0])
point2 = np.array([3, 4])
p_values = [1, 2, 3, 5, 10]
distances = []
for p in p_values:
dist = distance.minkowski(point1, point2, p)
distances.append(dist)
print(f"p={p}: 距離={dist:.2f}")
# 運行結果:
'''
p=1: 距離=7.00
p=2: 距離=5.00
p=3: 距離=4.50
p=5: 距離=4.17
p=10: 距離=4.02
'''
2. 第二門派:方向與相關性的探索者
這一類距離不關心 “數值大小”,更關心 “趨勢方向” 或 “統計關係”。
2.1. 餘弦距離:關注方向而非大小
餘弦距離衡量的是兩個向量方向的差異,而不是它們的大小差異。
這在文本分析中特別有用,因為文檔的長度不同,但主題可能相似。
應用場景:
- 文本相似度(熱點): 比如比較兩篇文章。文章 A 只有 100 字,文章 B 有 10000 字,雖然詞頻數值差很大,但如果它們都在講“人工智能”,它們的方向(角度)是一致的。
- 推薦系統: 用户打分偏好。
代碼示例:(用幾個簡單的新聞標題來計算餘弦相似度)
# 文本向量(假設是詞頻):[AI, 蘋果, 股票]
doc_1 = [10, 0, 5] # 科技財經文
doc_2 = [20, 0, 10] # 長篇科技財經文(方向一致)
doc_3 = [0, 10, 0] # 水果文
# 餘弦距離 = 1 - 餘弦相似度
# 接近0,表示非常相似
print(f"同類文章餘弦距離: {distance.cosine(doc_1, doc_2):.2f}")
# 接近1,表示無關
print(f"不同類文章餘弦距離: {distance.cosine(doc_1, doc_3):.2f}")
# 運行結果:
'''
同類文章餘弦距離: 0.00
不同類文章餘弦距離: 1.00
'''
2.2. 相關係數距離:衡量線性關係
基於皮爾遜相關係數的距離,衡量兩個變量之間線性相關性的差異。
應用場景:
- 股票分析: 衡量兩隻股票的走勢是否同步。如果一支漲另一支也漲,它們的相關距離就很小,哪怕一個股價是 10 元,另一個是 1000 元。
# 兩隻股票過去5天的漲跌幅
stock_A = [0.1, -0.2, 0.3, 0.1, 0.0]
stock_B = [0.2, -0.4, 0.6, 0.2, 0.0] # 走勢完全也就是2倍關係
d_correlation = distance.correlation(stock_A, stock_B)
print(f"相關係數距離: {d_correlation:.2f}")
# 運行結果
'''
相關係數距離: 0.00
'''
可以嘗試調整調整stock_A和stock_B的數值,再看看相關係數的變化。
2.3. 馬氏距離:考慮數據分佈的距離
馬氏距離考慮了數據的協方差結構,是一種尺度無關且排除了特徵相關性的距離度量。
應用場景:
- 異常檢測: 假設你統計人的身高和體重。如果你用歐氏距離,一個 190cm、50kg 的人可能離中心點不遠。但考慮到身高體重的正相關性(高的人通常重),這個數據點在馬氏距離下就會非常遠(非常異常)。
# 需要先計算協方差矩陣的逆
np.random.seed(42)
height = np.random.normal(170, 10, 20) # 20個身高樣本
weight = height * 0.5 + np.random.normal(0, 5, 20) # 體重與身高相關
data = np.column_stack([height, weight])
cov_matrix = np.cov(data.T)
inv_cov_matrix = np.linalg.inv(cov_matrix)
point_1 = [170, 60] # 正常點
point_2 = [190, 50] # 異常點(又高又瘦)
d_mah_1 = distance.mahalanobis(point_1, np.mean(data, axis=0), inv_cov_matrix)
d_mah_2 = distance.mahalanobis(point_2, np.mean(data, axis=0), inv_cov_matrix)
print(f"正常點馬氏距離: {d_mah_1:.2f}")
print(f"異常點馬氏距離: {d_mah_2:.2f}") # 距離會很大
# 運行結果:
'''
正常點馬氏距離: 4.93
異常點馬氏距離: 9.06
'''
3. 第三門派:集合與分類的裁判
當數據不是數字,而是分類、標籤或字符串時,我們用這些。
3.1. 傑卡德距離:集合的相似度
傑卡德距離衡量兩個集合的差異程度,通過計算交集與並集的比例得到。
應用場景:
- 電商推薦: 用户 A 買了 {蘋果, 香蕉},用户 B 買了 {蘋果, 香蕉, 西瓜}。通過傑卡德距離計算他們的購買重合度,進而推薦商品。
d_jaccard = distance.jaccard([1, 1, 0], [1, 1, 1]) # boolean vector
print(f"傑卡德距離: {d_jaccard:.2f}")
# 運行結果:
'''
傑卡德距離: 0.33
'''
3.2. 漢明距離:字符串的差異度量
漢明距離衡量兩個等長字符串在對應位置上不同字符的數量。
應用場景:
- 拼寫糾錯: "banana" 和 "banane",只有一個字母不同,漢明距離為 1。
- 信息編碼: 通信中檢測數據傳輸是否出錯。
d_hamming = distance.hamming([1, 0, 1], [1, 0, 0])
print(f"漢明距離: {d_hamming:.2f}") # 輸出比例,有些庫輸出個數
# 運行結果:
'''
漢明距離: 0.33
'''
3.3. 編輯距離:字符串轉換的代價
編輯距離(Levenshtein距離)衡量將一個字符串轉換為另一個字符串所需的最少單字符編輯操作次數(插入、刪除、替換)。
應用場景:
- 搜索引擎: 你輸錯單詞時,百度/谷歌提示“您是不是要找...”,就是通過編輯距離找到最接近的正確詞。
# 注:標準庫無此函數,通常用 pip install Levenshtein 或自定義
# 這裏用簡單的邏輯演示概念
def simple_levenshtein(s1, s2):
if len(s1) < len(s2):
return simple_levenshtein(s2, s1)
if len(s2) == 0:
return len(s1)
previous_row = range(len(s2) + 1)
for i, c1 in enumerate(s1):
current_row = [i + 1]
for j, c2 in enumerate(s2):
insertions = previous_row[j + 1] + 1
deletions = current_row[j] + 1
substitutions = previous_row[j] + (c1 != c2)
current_row.append(min(insertions, deletions, substitutions))
previous_row = current_row
return previous_row[-1]
print(f"編輯距離 ('kitten', 'sitting'): {simple_levenshtein('kitten', 'sitting')}")
# 運行結果:
'''
編輯距離 ('kitten', 'sitting'): 3
'''
4. 第四門派:分佈差異的鑑定師
用於衡量兩個“概率分佈”(比如兩個直方圖)有多像。這在機器學習和生成式 AI 中非常火。
4.1. KL 散度:衡量概率分佈差異
KL散度衡量一個概率分佈與另一個參考分佈之間的差異,但不是對稱的。
應用場景:
- 機器學習訓練: 衡量模型預測的概率分佈與真實標籤分佈之間的差異(Loss Function)。
from scipy.stats import entropy
p = [0.1, 0.9] # 真實分佈
q = [0.2, 0.8] # 預測分佈
kl_div = entropy(p, q)
print(f"KL散度: {kl_div:.4f}")
# 運行結果:
'''
KL散度: 0.0367
'''
4.2. JS 散度:衡量概率分佈差異-對稱
JS散度是KL散度的對稱版本,值域固定。
應用場景:
- GAN (生成對抗網絡): 早期用於衡量生成圖片分佈與真實圖片分佈的相似度。
d_js = distance.jensenshannon(p, q)
print(f"JS散度: {d_js:.4f}")
# 運行結果:
'''
JS散度: 0.0998
'''
4.3. Wasserstein 距離:地球搬運距離
Wasserstein距離衡量將一個概率分佈"搬運"成另一個所需的最小工作量,直觀理解是將一堆沙子變成指定形狀所需的最小移動距離。
應用場景:
- 圖像生成 (WGAN): 即使兩個分佈完全不重疊(KL 散度會失效),Wasserstein 距離也能給出合理的數值,指導 AI 學習。
from scipy.stats import wasserstein_distance
d_wasserstein = wasserstein_distance([0, 1, 3], [5, 6, 8])
print(f"Wasserstein距離: {d_wasserstein:.2f}")
# 運行結果:
'''
Wasserstein距離: 5.00
'''
5. 第五門派:時間序列的變形者
5.1. DTW 距離:時間序列的彈性匹配
動態時間規整(DTW)距離允許時間軸伸縮彎曲,用於衡量兩個時間序列的相似性,即使它們在時間軸上不完全對齊。
應用場景:
- 語音識別/股票分析: 兩個人讀同一個單詞 "Hello"。
- 人 A:H-e-l-l-o (語速快)
- 人 B:H-e-e-e-l-l-o-o (語速慢)
- 歐氏距離會認為這完全不同,但 DTW 會把時間軸“對齊”,發現它們其實很像。
# 簡單的DTW概念代碼(實際應用推薦使用 fastdtw 庫)
from scipy.spatial.distance import euclidean
def dtw_distance(s1, s2):
n, m = len(s1), len(s2)
dtw_matrix = np.zeros((n+1, m+1))
dtw_matrix[0, 1:] = np.inf
dtw_matrix[1:, 0] = np.inf
for i in range(1, n+1):
for j in range(1, m+1):
cost = abs(s1[i-1] - s2[j-1])
dtw_matrix[i, j] = cost + min(dtw_matrix[i-1, j], # 插入
dtw_matrix[i, j-1], # 刪除
dtw_matrix[i-1, j-1]) # 匹配
return dtw_matrix[n, m]
ts_1 = [1, 2, 3, 4]
ts_2 = [1, 1, 2, 3, 4, 4] # 同樣趨勢,但多了重複(慢動作)
print(f"DTW距離: {dtw_distance(ts_1, ts_2)}")
# 運行結果:
'''
DTW距離: 0.0
'''
6. 總結:如何選擇你的“尺子”?
面對新數據,別盲目選歐氏距離,參考下面的建議:
- 普通數值數據,看絕對大小: 選 歐氏 或 曼哈頓。
- 看重方向/喜好,忽略絕對數值: 選 餘弦距離(如文本、推薦)。
- 看重趨勢變化,忽略數值大小: 選 相關係數距離(如股票)。
- 數據相關性強,且有離羣點: 選 馬氏距離。
- 集合、標籤類數據: 選 傑卡德 或 漢明。
- 概率分佈對比(AI 模型): 選 KL 或 Wasserstein。
- 長短不一的時間序列: 選 DTW。
文中代碼中大部分的距離關鍵是掌握其概念和應用場景,至於其距離算法的實現,scipy庫中大部分都有封裝好的函數,即使沒有,也可以用其他庫來代替。