本文由 Ververica 首席架構師 Giannis Polyzos 撰寫，__探討了流與表的“二元性”本質，澄清常見誤解，指出 Kafka 與 Iceberg 等系統在缺乏主鍵和變更語義時無法真正實現該二元性，並強調統一系統對流表融合的重要性。

什麼是流/表二元性？

核心思想其實很簡單：

• 流（Stream） 是一個永不停止的變更日誌 📜。
• 表（Table） 是這些變更的物化視圖，即當前狀態 🗄️。

👉 任何表都可以表示為一個更新流。  👉 任何更新流也可以物化成一張表。

舉個例子：

• 數據庫發出 INSERT、UPDATE 和 DELETE 事件 → 這就是一個流。
• 按順序應用這些事件，就能重建出原始的表。
• 反過來，捕獲表的每一次變更 → 就能得到變更日誌流（changelog stream）。

這就是雙向映射，也就是所謂的“二元性”💡。

二元性的核心前提

要讓這種“魔法”成立，必須滿足以下條件：

• 變更日誌語義（Changelog semantics）：流不僅要包含新增記錄，還必須攜帶更新（UPDATE）和刪除（DELETE）操作。
• 主鍵（Primary keys）：系統需要知道要更新哪一行。
• 時間是一等公民：流提供事件的順序，表則代表“在時間 T 的狀態”。
• 物化能力（Materialization）：表本質上是流的一個物化視圖。
• 一致性（Consistency）：重放相同的流，始終能得到相同的表。

二元性何時會失效？

事情有趣的地方就在這裏。當前社區中，很多人試圖將 Apache Kafka 與 Apache Iceberg 的集成描述為“流/表二元性”，但事實並非如此。我們來拆解一下：

Apache Iceberg

Iceberg 是一個優秀的開源表格式，特別適合管理僅追加（append-only） 的數據。

但請注意：

• ❌ 不強制要求主鍵
• ❌ 原生不支持流式場景下的行級更新或刪除

這意味着你無法獲得真正的流/表二元性——你只能拿到一系列快照（snapshots），而不是持續演化的狀態。

Apache Kafka

Kafka 本質上是一個事件日誌（event log），不是變更日誌（changelog）。

默認情況下：

• 它只存儲原始事件；
• 沒有更新或刪除的概念。

所以：

• ❌ Kafka 本身 ≠ changelog 流

不過……

藉助 Debezium 或 Flink CDC

• 你可以從數據庫捕獲真正的變更事件（包含主鍵和操作類型）；
• Kafka Topic 此時才真正承載了變更日誌流；
• Flink 等引擎就能基於這些流物化出表。

關鍵點：Kafka 本身不是 changelog，這點必須強調，因為這直接影響下游處理的複雜度。

像 Apache Flink 這樣的流處理引擎，其核心正是建立在 changelog 模型之上的。

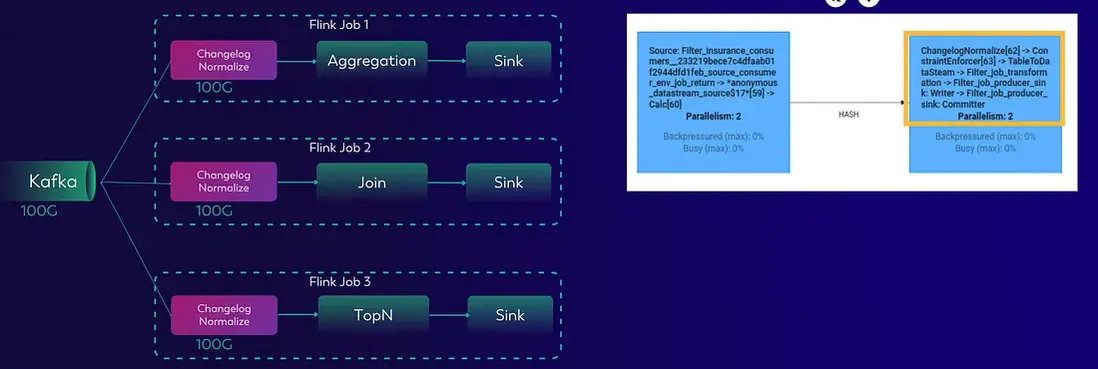
由於 Kafka 不原生提供 changelog，Flink 必須引入一個昂貴的算子（如 ChangelogNormalize）來對 Kafka 數據進行歸一化處理——這會導致：

• 狀態膨脹
• 冗餘存儲

更糟糕的是，這個歸一化後的 changelog 無法複用。   如果你有多個作業消費同一個 Kafka Topic，每個作業都得各自重建並存儲一份 changelog 狀態。

那麼，流和表必須在同一個系統裏嗎？

這是我一直在思考的問題。

確實，很多系統天然支持流/表二元性，比如：

• PostgreSQL、MySQL（通過邏輯複製）
• Apache Beam
• 以及我深度參與的 Apache Flink、Apache Paimon，還有最近的 Apache Fluss

所以，我傾向於認為：“最好在同一個系統內實現”。

否則，你只是在做兩個無法原生支持二元性的系統之間的集成。

不過，由於目前尚無“流/表二元性”的正式定義，答案也可以是：不一定。

像 Flink、Kafka Streams 等系統，在同一個引擎中同時暴露流和表 API，讓二元性變得無縫。  但理論上，你也可以用不同系統實現——只要保證事件順序、主鍵和 changelog 語義不丟失，二元性依然成立。

但基於前文分析，我認為將 Kafka + Iceberg 的組合稱為“流/表二元性”是不嚴謹的。

總結

• 流 = 故事（所有發生過的事件）
• 表 = 快照（當前的真實狀態）

二者共同構成了現代實時分析、流處理和湖倉一體架構的基石。

但請務必警惕：

• ❌ Kafka ≠ changelog（除非結合 CDC）
• ❌ Iceberg ≠ 表二元性（無主鍵，僅支持追加）

當然，業界還有更多關於這一話題的演進和不同技術路線，但本文暫且聚焦於此。

PS：如果你正在尋找一個真正基於上述原則構建的系統，並希望獲得額外能力（如直接查詢流、內置緩存等），不妨關注一下 Apache Fluss。

繼續奔涌吧 🌊🤘

更多內容

活動推薦

複製下方鏈接或者掃描二維碼
即可快速體驗 “一體化的實時數倉聯合解決方案”
瞭解活動詳情：https://www.aliyun.com/solution/tech-solution/flink-hologres