【問題】
如圖所示,由足夠長的平行金屬導軌構成的斜面,傾角α=37°,導軌間距L=0.5m,電阻不計;沿導軌方向建立x軸,虛線EF與座標原點O在同一水平線上;空間存在垂直於斜面的磁場,取垂直於斜面向上為正方向,其磁感應強度的分佈為x<0時B=-1(T),x>=0時B=0.6+0.8x(T).
現有一質量為m1=0.1kg,電阻R1=0.2Ω的金屬棒ab放置於導軌上,下方還有質量m2=0.3kg,邊長均為L的U形框cdef,其中金屬棒de的電阻R2=0.2Ω,cd,ef兩棒是絕緣的,金屬棒,U形棒與導軌間的動摩擦因數μ=0.75,最大靜摩檫力=滑動摩檫力。
現給ab棒一個沿斜面向下的瞬時衝量,g取10m/s^2.問:
(1)若I0=0.6N*S,求此瞬間金屬棒ab上感應電流的方向和電勢差Uab;
(2)為使棒框碰撞前U形框能保持靜止,求I0應滿足的條件;
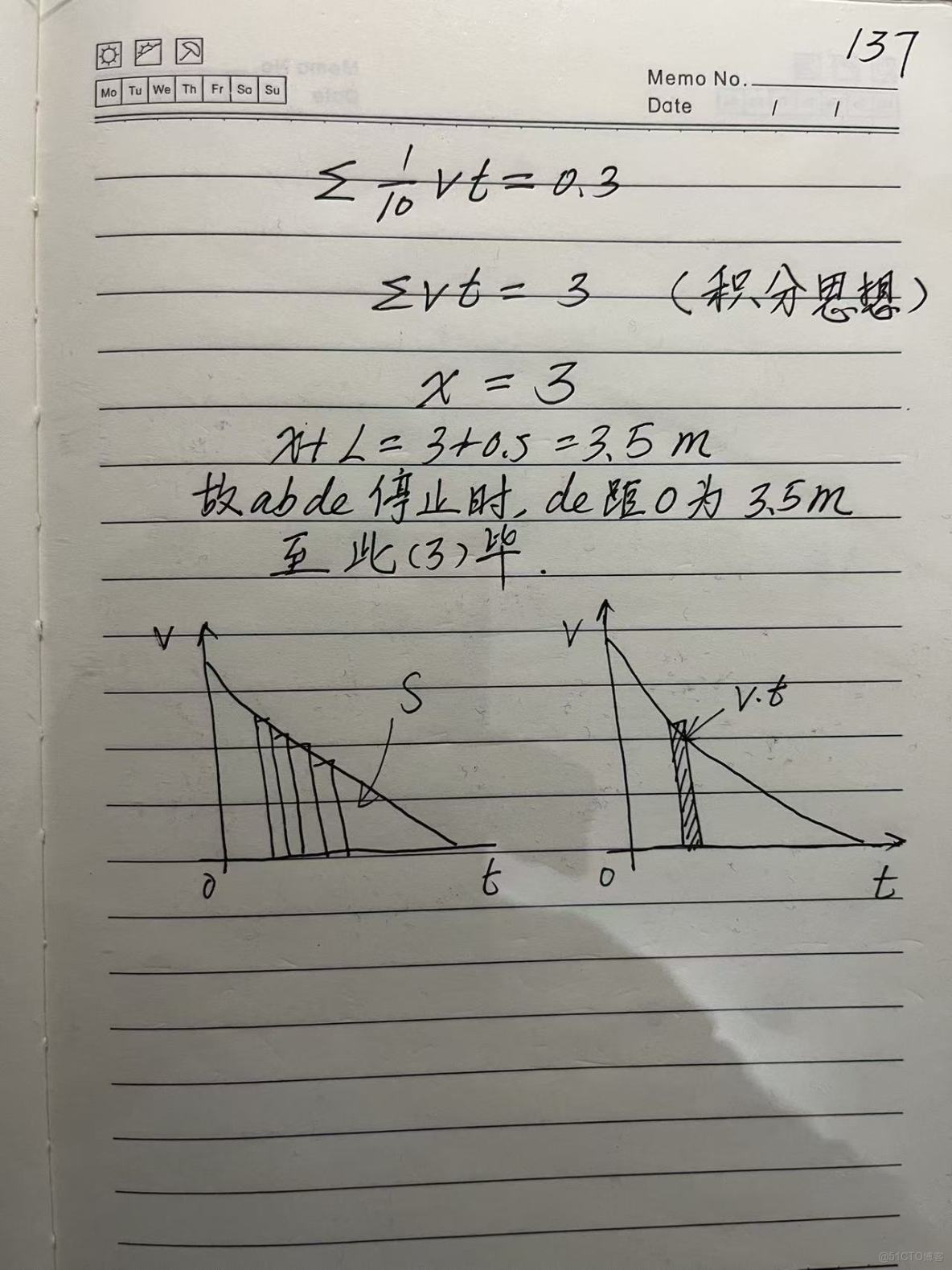
(3)若金屬棒ab位於x=-0.32m處,當I0=0.5N*S時,金屬棒ab與U形框發生完全非彈性碰撞,求最終靜止時de邊的座標。
【答案】
(1) b->a,1.5v
(2) <=0.576
(3) 3.5m
【解答】
【點評】
第三問的積分思想有點超綱。