特徵選擇的目的
- 提高模型準確率:移除冗餘、不相關或噪聲特徵,使模型更專注於有效信息,減少過擬合的風險。
- 降低計算成本:減少特徵數量可以加快模型的訓練和預測速度。
- 增強模型可解釋性:使用更少的特徵可以更容易地理解特徵與目標變量之間的關係。
- 緩解維度災難:當特徵數量遠大於樣本數量時,模型容易陷入局部最優,特徵選擇可以有效緩解這一問題。
常用方法
特徵選擇方法主要分為三大類:過濾式、包裹式和嵌入式。
1.過濾式
過濾式方法獨立於任何特定的學習算法,僅僅通過特徵自身的統計特性或特徵與目標變量之間的關係(如方差、與目標變量的相關性等)來評分,然後選擇得分最高的特徵。
常用的方法有
- 方差選擇法
移除方差低於某一閾值的特徵。低方差意味着特徵在所有樣本中的取值變化不大,區分度低,對模型的貢獻小。 - 相關係數
用於衡量特徵 與目標變量 之間的線性關係強度。常用的有皮爾遜相關係數。 - 卡方檢驗
用於檢驗分類問題中離散特徵和類別之間的獨立性。
卡方值越大,獨立性假設越不成立,即特徵與目標越相關。 - 互信息/信息增益
衡量特徵 和目標變量 之間的依賴性。互信息越高,特徵的預測能力越強。
優點: 計算速度快,獨立於模型
缺點: 忽略了特徵之間的相互作用
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectKBest, chi2, RFE, VarianceThreshold
from sklearn.linear_model import LogisticRegression, LassoCV
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import accuracy_score
# 加載數據
iris = load_iris()
X = iris.data
y = iris.target
feature_names = iris.feature_names
X = MinMaxScaler().fit_transform(X) # 特徵歸一化,通常對某些方法有益
# 轉換為 DataFrame 方便操作
df = pd.DataFrame(X, columns=feature_names)
## 過濾式:卡方檢驗 (SelectKBest with chi2)
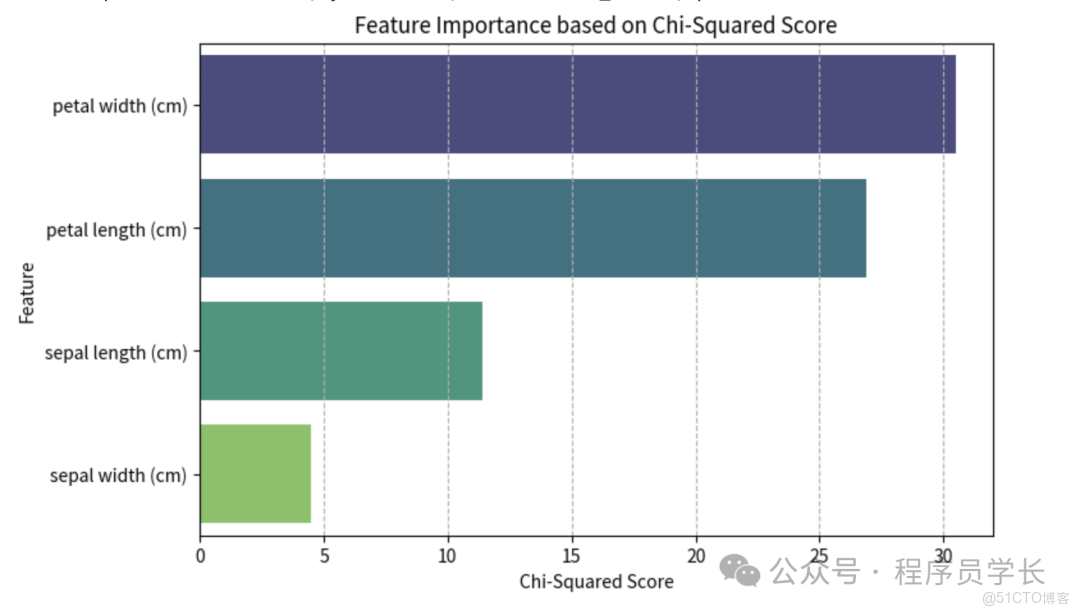
print("="*10, "1. 過濾式:卡方檢驗", "="*10)
# 1. 計算所有特徵的卡方值
chi2_scores, p_values = chi2(X, y)
# 2. 創建結果 DataFrame
feature_scores = pd.DataFrame({
'Feature': feature_names,
'Chi2 Score': chi2_scores,
'P-Value': p_values
}).sort_values(by='Chi2 Score', ascending=False)
print(feature_scores)
# 3. 使用 SelectKBest 選出K=2個最佳特徵
k = 2
selector = SelectKBest(chi2, k=k)
X_new_chi2 = selector.fit_transform(X, y)
selected_features_chi2 = [feature_names[i] for i in selector.get_support(indices=True)]
print(f"\n選出的 {k} 個最佳特徵: {selected_features_chi2}")
# 4. 可視化:特徵卡方值排名
plt.figure(figsize=(8, 5))
sns.barplot(x='Chi2 Score', y='Feature', data=feature_scores, palette="viridis")
plt.title('Feature Importance based on Chi-Squared Score')
plt.xlabel('Chi-Squared Score')
plt.ylabel('Feature')
plt.grid(axis='x', linestyle='--')
plt.show()包裹式
包裹式方法使用模型性能作為評價標準。
它將學習器(模型)作為一個黑箱,特徵選擇過程是圍繞模型展開的。它通過不斷嘗試不同的特徵子集,並使用目標學習器來評估這些子集的性能(如交叉驗證誤差),從而選擇最佳子集。
常用的方法有
- 前向選擇
從空集開始,每次添加一個能使模型性能提升最大的特徵,直到性能不再顯著提高或達到預設特徵數。 - 後向消除
從所有特徵的集合開始,每次移除一個對模型性能影響最小的特徵,直到性能不再顯著提高或達到預設特徵數。 - 遞歸特徵消除 (RFE)
首先在完整特徵集上訓練一個模型(如線性模型),然後根據特徵係數或重要性排名,遞歸地移除最不重要的特徵,直到所需的特徵數量。
優點: 考慮到特徵的組合效應,選擇的特徵子集往往能帶來更好的模型性能。
缺點: 計算量巨大,需要多次訓練模型,速度慢。
## 包裹式:遞歸特徵消除 (RFE)
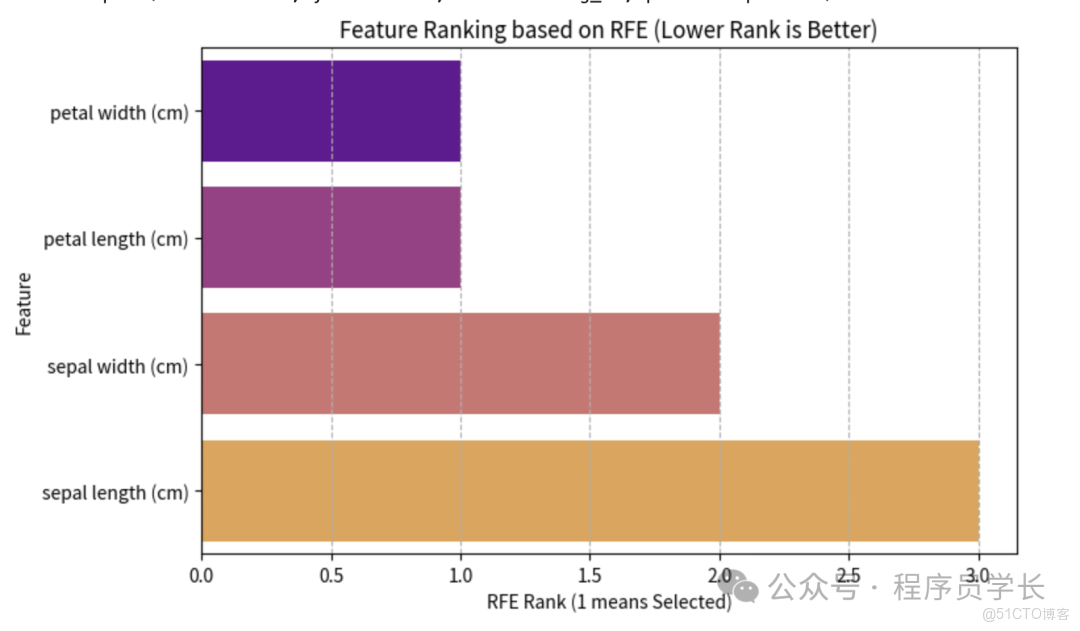
print("\n"+"="*10, "2. 包裹式:遞歸特徵消除 (RFE)", "="*10)
# 1. 初始化分類器(評估器)和 RFE
# 邏輯迴歸常用於RFE,因為它提供可解釋的係數(權重)
estimator = LogisticRegression(solver='liblinear')
# 目標是選出 k=2 個特徵
k = 2
rfe_selector = RFE(estimator, n_features_to_select=k, step=1)
# 2. 執行 RFE
rfe_selector.fit(X, y)
# 3. 獲取選中的特徵和特徵排名
selected_features_rfe = [feature_names[i] for i in rfe_selector.get_support(indices=True)]
feature_rankings = rfe_selector.ranking_
print(f"選出的 {k} 個最佳特徵: {selected_features_rfe}")
# 4. 可視化:特徵排名
ranking_df = pd.DataFrame({
'Feature': feature_names,
'RFE Rank': feature_rankings
}).sort_values(by='RFE Rank', ascending=True)
plt.figure(figsize=(8, 5))
sns.barplot(x='RFE Rank', y='Feature', data=ranking_df, palette="plasma")
plt.title('Feature Ranking based on RFE (Lower Rank is Better)')
plt.xlabel('RFE Rank (1 means Selected)')
plt.ylabel('Feature')
plt.grid(axis='x', linestyle='--')
plt.show()3.嵌入式
嵌入式方法將特徵選擇過程與模型訓練過程融為一體,在模型訓練的過程中自動進行特徵選擇。
常用的方法有
- L1 正則化
在損失函數中添加 L1 範數作為懲罰項。L1 範數傾向於將不重要特徵的係數壓縮為零,從而實現特徵選擇。 - 樹模型特徵重要性
基於決策樹、隨機森林 (Random Forest)、梯度提升樹 (GBDT/XGBoost) 等模型。
這些模型在構建時會計算每個特徵對分裂(例如,基尼不純度或信息增益)的貢獻度。貢獻度越高,特徵重要性越高。
## 嵌入式:Lasso 迴歸 (L1 正則化)
print("\n"+"="*10, "3. 嵌入式:Lasso (L1 正則化)", "="*10)
# 由於 Lasso 是迴歸模型,我們在這裏將其應用於目標編碼後的多分類(簡單演示)
# 通常Lasso更常用於迴歸問題,但在多分類任務中,可以分別對每個類別進行二元分類處理。
# 為簡化示例,我們直接在多分類數據集上使用 LassoCV。
# 1. 初始化 LassoCV (內置交叉驗證自動選擇最佳alpha)
# max_iter 增加迭代次數以確保收斂
lasso = LassoCV(cv=5, random_state=42, max_iter=10000).fit(X, y)
# 2. 獲取最佳 alpha 值下,每個特徵的係數 (權重)
coefficients = lasso.coef_
# 3. 創建結果 DataFrame
coef_df = pd.DataFrame({
'Feature': feature_names,
'Coefficient': coefficients
}).sort_values(by='Coefficient', key=abs, ascending=False) # 按係數絕對值排序
# 4. 選出係數不為零的特徵
selected_features_lasso = coef_df[coef_df['Coefficient'].abs() > 1e-6]['Feature'].tolist()
print(f"LassoCV 選出的非零係數特徵: {selected_features_lasso}")
# 5. 可視化:特徵係數
plt.figure(figsize=(8, 5))
sns.barplot(x='Coefficient', y='Feature', data=coef_df, palette="coolwarm")
plt.axvline(x=0, color='grey', linestyle='--') # 標記係數零線
plt.title('Feature Coefficients from Lasso Regression')
plt.xlabel('Coefficient Value')
plt.ylabel('Feature')
plt.grid(axis='x', linestyle='--')
plt.show()