如果一個項目的核心不是分類準確率，而是概率估計的質量。換句話説，需要的是一個校準良好的模型。這裏校準的定義是：如果模型給一批樣本都預測了25%的正例概率，那這批樣本中實際的正例比例應該接近25%。這就是校準。

解決這個校準問題單看ROC-AUC不夠，要用Brier score或者Log-loss來保證校準質量。

我們先介紹一下我們一般使用的的幾個指標：

ROC-AUC衡量的是模型區分正負樣本的排序能力，跟預測概率的絕對值無關。

Brier score本質上就是預測概率的均方誤差：

1. =np.mean((y_proba-y_true)**2)

Log-loss則是從似然的角度評估概率質量：

1. =-np.mean(y_true*np.log(y_proba)+(1-y_true)*np.log(1-y_proba))

這裏用PyCaret的Bank數據集做演示：隨機抽取100組不同的特徵子集，每組特徵分別訓練4種模型（Logistic Regression、Decision Tree、Random Forest、LightGBM），得到400個候選模型。所有指標都在獨立的測試集上計算。

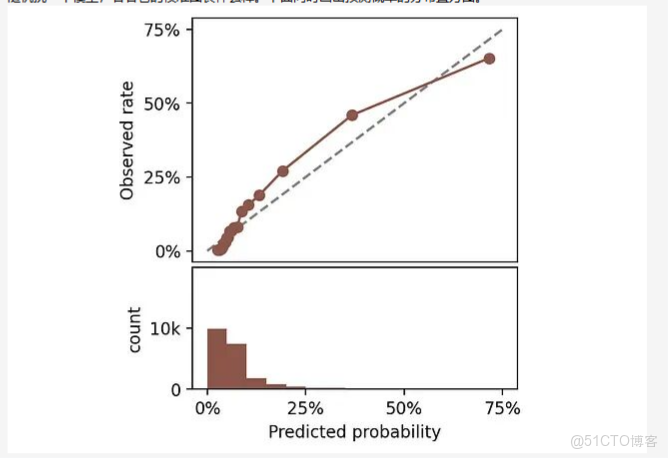
校準圖的可視化邏輯

評估校準最直觀的方式是畫校準圖。方法是把預測概率分成若干區間，每個區間內比較平均預測概率（x軸）和實際正例比例（y軸）。

隨機挑一個模型，看看它的校準圖長什麼樣。下面同時畫出預測概率的分佈直方圖。

頂部：校準圖。底部：預測概率直方圖。

完美校準的模型，曲線應該貼着45度對角線。比如某個區間平均預測概率是25%，那這個區間裏實際正例比例也該是25%。曲線偏離對角線越遠説明校準越差。