在實際應用中，我們經常會使用到功率MOS，這時通常不會將它當成一個開關使用，而是當成一個放大器來使用，那這就需要讓其工作在放大狀態。

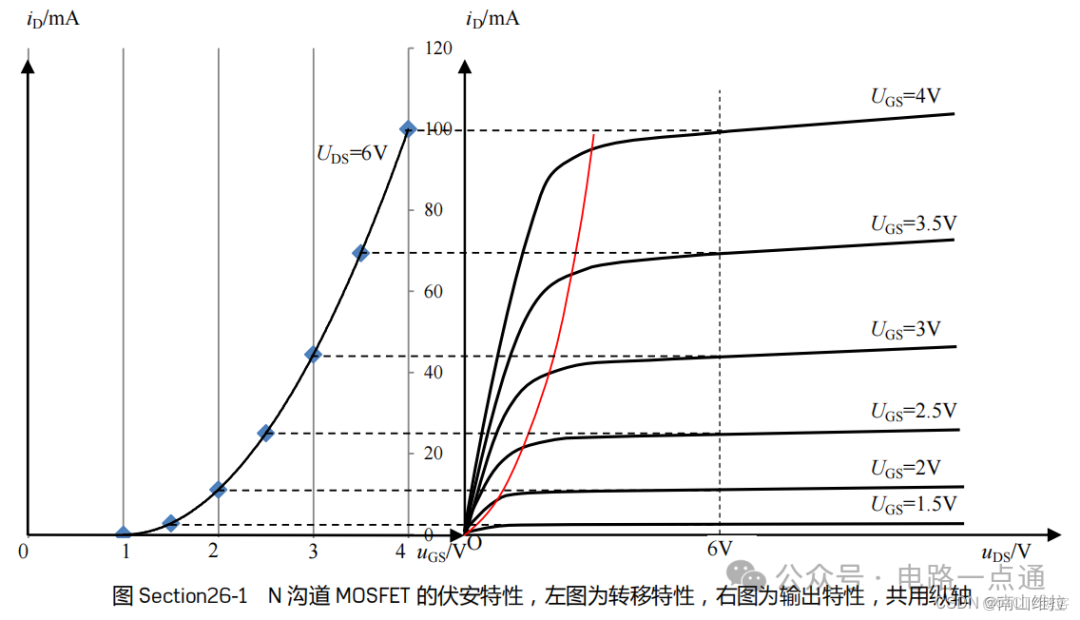
參考下圖中的mos管的特性曲線，右圖中的輸出特性曲線中有一根紅色的分界線，這個線就是區分mos管工作狀態的分界線，在紅線的左邊，mos管工作在可變電阻區，也就是線性區；在紅線的右邊mos管工作在恆流區，也就是飽和區。當然，還有一個截止區。

本文分析主要運用模電課本中的理論計算驗證。

1.三電阻電路

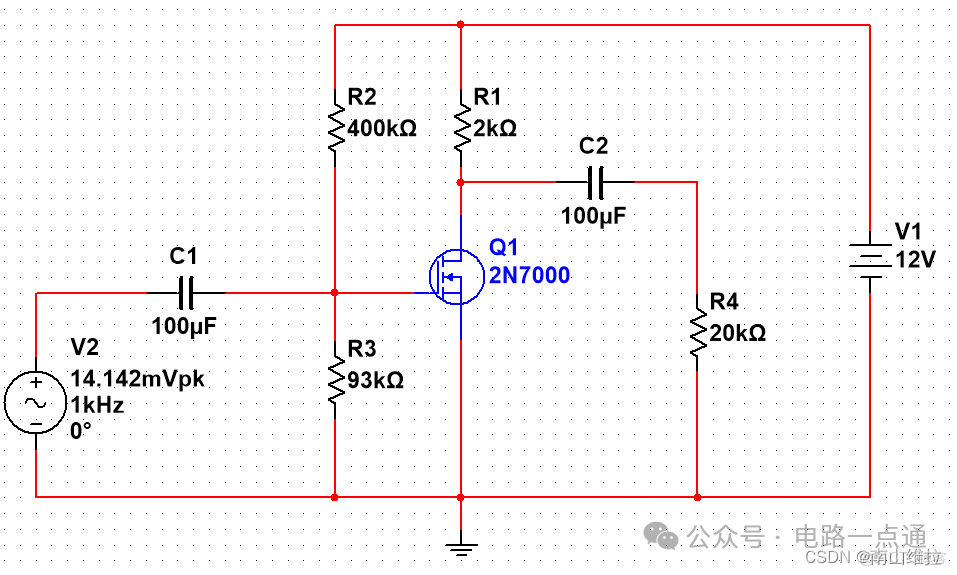
如上圖所示，是在multisim中繪製的放大電路，便於仿真驗證。使用的MOS管的型號為2N7000。計算中需要使用的關鍵參數

U G S T H = 2 V U_{GSTH}=2V UGSTH=2V K = 0.0502 A / V 2 K=0.0502A/V^{2} K=0.0502A/V2

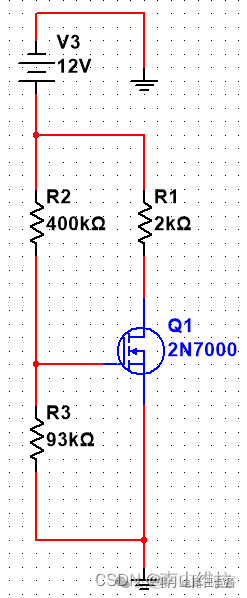
第一步判斷此MOS是否工作在放大狀態？那麼就需要先分析其靜態。分析靜態的時候，電容開路，那麼就會簡化電路如下：

MOS管柵極電壓用電阻分壓可以求得

U G Q = 12 V ∗ R 3 / ( R 2 + R 3 ) = 2.26 V U_{GQ}=12V*R3/(R2+R3)=2.26V UGQ=12V∗R3/(R2+R3)=2.26V （1）

這裏的源極也就是S極直接接地了，所以可以得到

U G S Q = U G Q = 2.26 V U_{GSQ}=U_{GQ}=2.26V UGSQ=UGQ=2.26V （2）

然後需要藉助下面這個公式（3）

I D Q = K ∗ ( U G S Q − U G S T H ) 2 = 3.49 m A I_{DQ}=K*(U_{GSQ}-U_{GSTH})^{2}=3.49mA IDQ=K∗(UGSQ−UGSTH)2=3.49mA（3）

（3）式是MOS管轉移特性曲線的方程，式中這個K值是個比較關鍵的點，我們後面分析。

U D S Q = 12 V − R 1 ∗ I D Q = 5.02 V U_{DSQ}=12V-R1*I_{DQ}=5.02V UDSQ=12V−R1∗IDQ=5.02V （4）

以上這幾個公式求出來的值就是MOS管在靜態工作時的幾個關鍵參數。

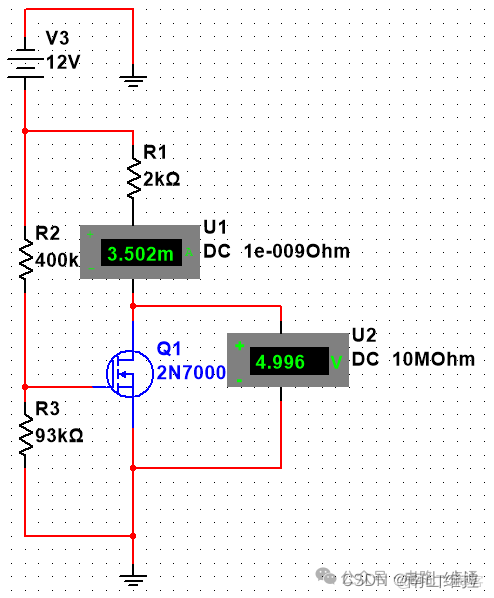
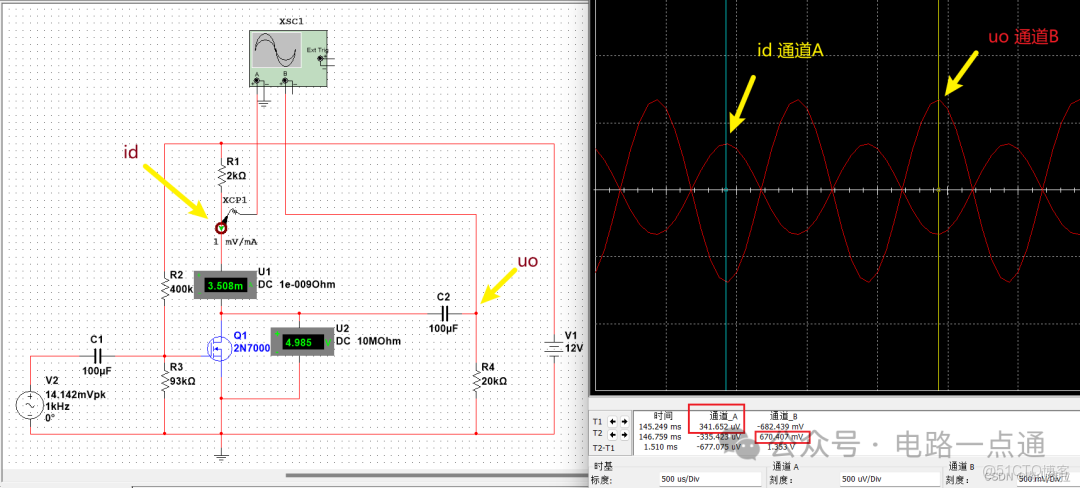
我們可以先在仿真中驗證一下正確性：

如上圖，我們在電路中串入一個直流電流表測量電路中的 I D Q I_{DQ} IDQ;並聯一個直流電壓表測量 U D S Q U_{DSQ} UDSQ。將兩個表測量的值和上面計算出來的值對比發現，結果非常接近，説明計算正確。

接下來是判斷MOS管的工作狀態：

在本例中，由上面計算得到的靜態參數可以進行下面的計算驗證。

U D S Q > U G S Q − U G S T H U_{DSQ}>U_{GSQ}-U_{GSTH} UDSQ>UGSQ−UGSTH （5）

當滿足該條件時，MOS管即工作在放大狀態，當然，前提條件是

U G S Q > U G S T H U_{GSQ}>U_{GSTH} UGSQ>UGSTH保證當前MOS處於導通狀態。

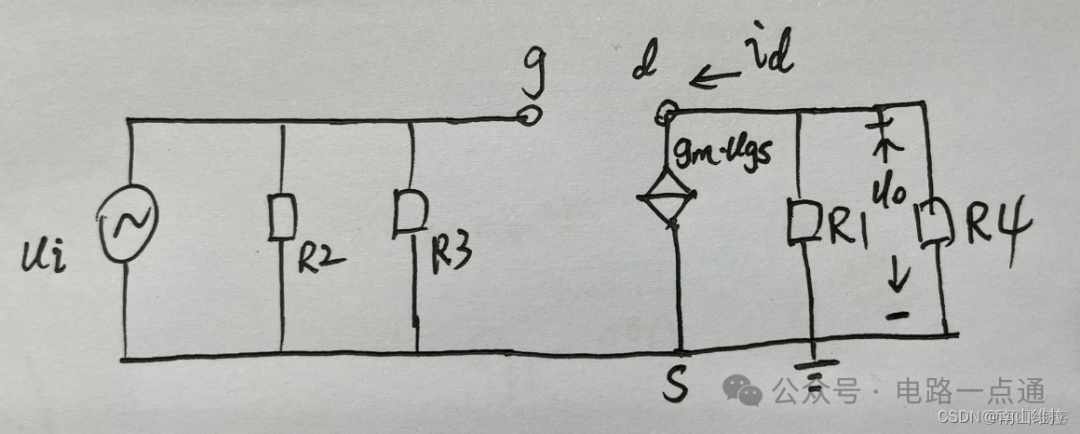
下面是小信號的動態等效電路分析：

該等效電路是對MOS管模型的等效，等效出一個壓控電流源，即 u g s u_{gs} ugs控制 i d i_{d} id，也就是圖中的

i d = g m ∗ u g s i_{d}=g_{m}*u_{gs} id=gm∗ugs（6）

該等式我們要注意兩點：

①注意等式中使用的字母和下標都是小寫，表明這裏的值都是純交流，沒有直流信號

②式中的 g m g_{m} gm表示跨導，即MOS管的轉移特性曲線的斜率。小信號的等效就説明輸入信號是一個幅值很小的信號，往往分析的時候就是計算在靜態工作點Q處的 g m g_{m} gm。

g m = 2 ∗ K ∗ I D Q g_{m}=2*\sqrt{K*I_{DQ}} gm=2∗K∗IDQ（7）

g m = 2 ∗ 0.0502 A / V 2 ∗ 3.49 m A = 26.47 m A / V g_{m}=2*\sqrt{0.0502A/V^{2}*3.49mA}=26.47mA/V gm=2∗0.0502A/V2∗3.49mA =26.47mA/V

至此，計算中需要用到的一些公式參數基本都出現了，接下來開始計算驗證。

首先計算一下 i d i_{d} id

i d = g m ∗ u g s = 2 ∗ 0.0502 A / V 2 ∗ 3.49 m A ∗ u i i_{d}=g_{m}*u_{gs}=2*\sqrt{0.0502A/V^{2}*3.49mA}*u_{i} id=gm∗ugs=2∗0.0502A/V2∗3.49mA ∗ui

這裏我只計算幅值， i d p k = 374.37 u A i_{_dpk}=374.37uA idpk=374.37uA

然後計算信號放大倍數

A V = u o u i = − 48.126 A_{V}=\frac{u_{o}}{u_{i}}=-48.126 AV=uiuo=−48.126

則對於輸入信號 u i p k = 14.142 m V u_{ipk}=14.142mV uipk=14.142mV

u o p k = − 48.126 ∗ 14.142 m V = − 680.599 m V u_{_opk}=-48.126*14.142mV=-680.599mV uopk=−48.126∗14.142mV=−680.599mV

觀察仿真波形：

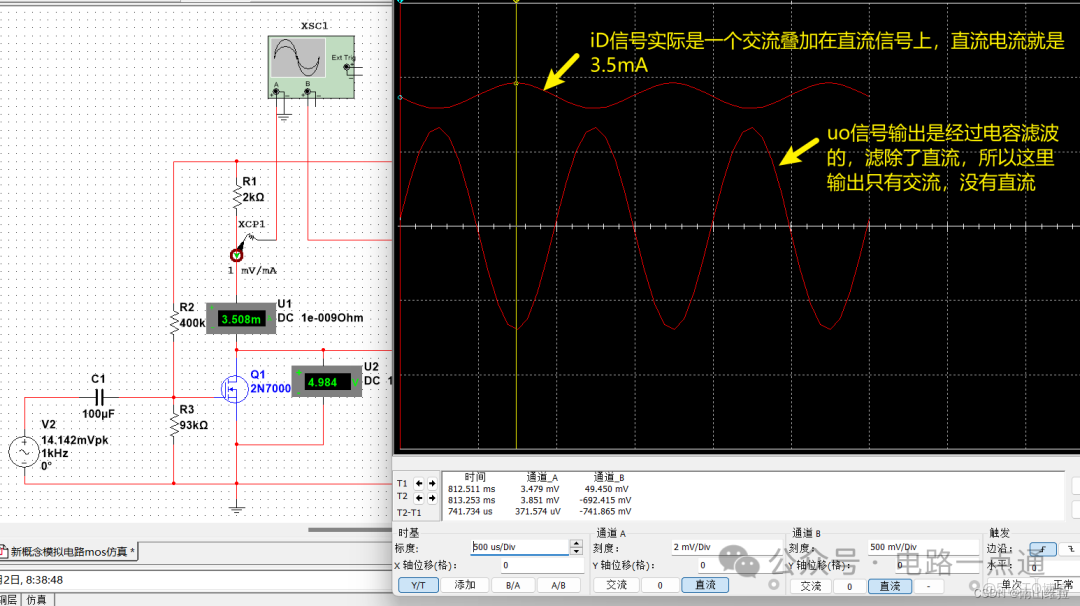
可以看到，這裏主要觀察了 i d i_{d} id和 u o u_{o} uo的值，我們看到這裏的兩個幅值和計算的幅值相差無幾，説明整個分析過程正確。注意波形圖中設置的是交流形式，意即沒有包含直流信號。如果我們調整為觀察交直流信號。

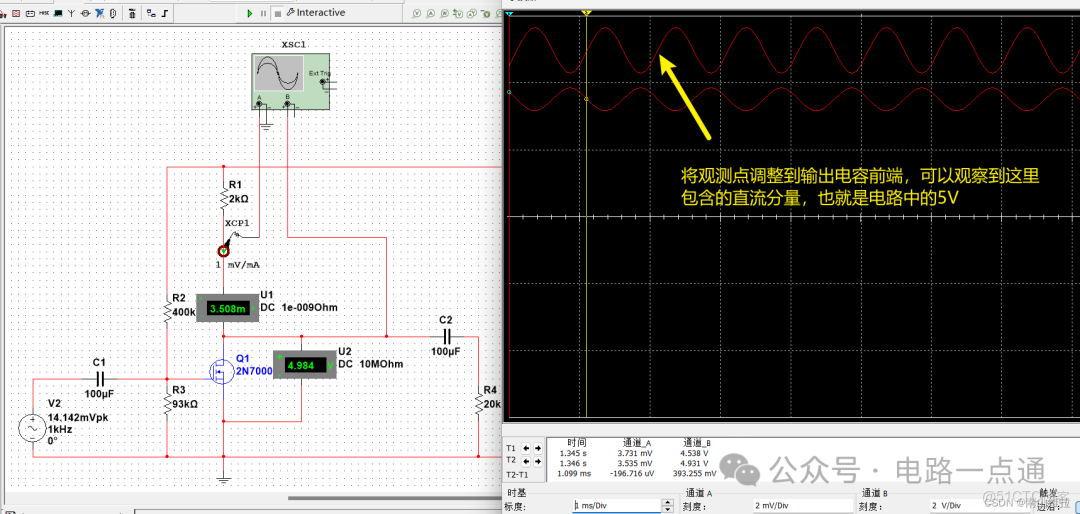
u o u_{o} uo輸出信號是經過電容濾波之後的信號，沒有直流信號。我們調整觀察點到電容前端，就可以觀察到直流信號，如下圖所示：

至此我們簡單分析了基於三電阻的MOS管放大電路的計算。分析中涉及到的理論計算均來自模擬電路課本，參考包括楊老師的新概念等。

針對計算中給出的 K K K值,在考試中往往會給出該值，所以計算較為方便。但是在實際應用電路中，在某個MOS的datasheet中是不會給出該值的，所以往往會無法計算。結合楊老師在新概念課堂中的建議，可以在對應的轉移特性曲線上取一點，找出對應的 u G S u_{GS} uGS和 i D i_{D} iD的值，可以求解出一個 K K K值。

但是在實際分析電路中可知，針對不同點，求解出的 K K K值相差比較大，因此在實際應用中，會存在一定偏差。