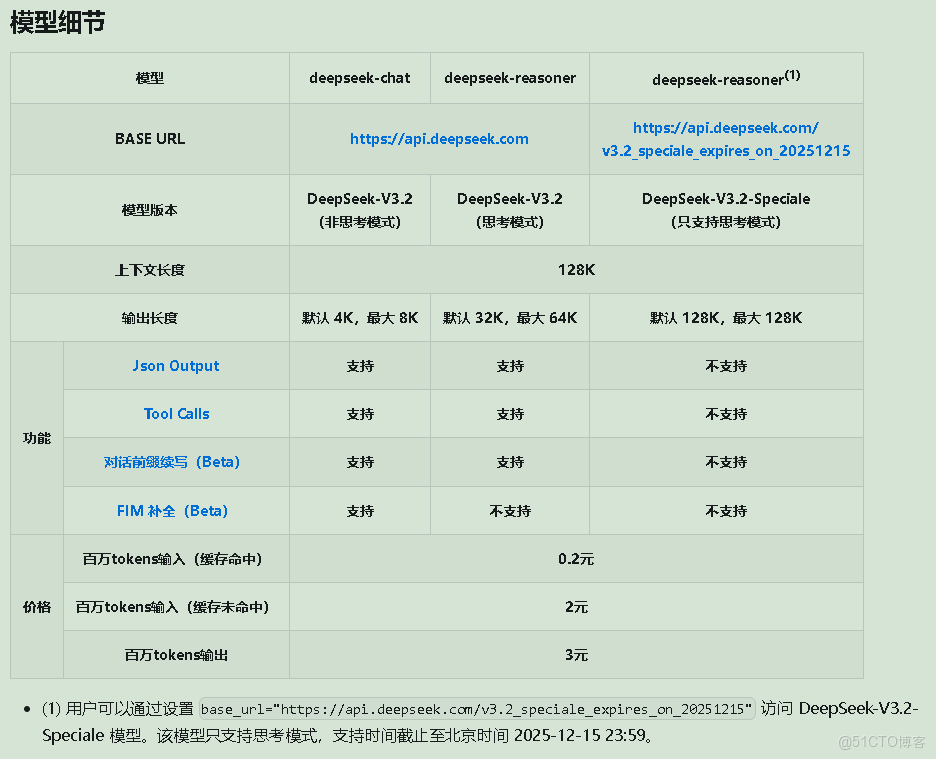
12 月 1 日,國產大模型廠商 DeepSeek 正式發佈雙模型版本 ——DeepSeek-V3.2(標準版) 與 DeepSeek-V3.2-Speciale(專業版),分別瞄準通用場景落地與頂尖技術研究需求,引發行業廣泛關注。
作為面向大眾用户的主力版本,DeepSeek-V3.2 核心優勢在於推理能力與輸出效率的極致平衡:官方數據顯示,其在公開基準測試(如 MMLU、GSM8K 等)中表現已逼近 GPT-5 水平,僅略遜於 Gemini-3.0-Pro;相較於同類長文本模型 Kimi-K2-Thinking,該版本大幅降低了計算資源佔用與響應延遲,兼顧性能與實用性。目前,DeepSeek-V3.2 已全面覆蓋網頁端、移動應用及 API 接口,普通用户可直接通過官方平台體驗,適用於智能問答、通用智能體開發等場景。
針對專業研究與高端場景,DeepSeek 同步推出 DeepSeek-V3.2-Speciale,現階段僅以臨時 API 形式開放測試,普通用户暫無法直接體驗。該版本的核心突破在於頂尖賽事級任務表現:不僅在主流推理基準測試中與 Gemini-3.0-Pro 持平,更在 2025 年國際數學奧林匹克(IMO)、國際信息學奧林匹克(IOI)、ICPC 世界總決賽及中國數學奧林匹克(CMO)等頂級學術競賽中斬獲金牌級成績,展現出極強的複雜問題求解能力。作為技術愛好者,筆者已第一時間申請測試權限並完成初步驗證。
測試代碼如下:
import requests
import json
import time
# 1. 配置API (注意:V3.2-Speciale使用臨時endpoint)
API_KEY = "" # 請替換為實際密鑰
API_URL = "https://api.deepseek.com/v3.2_speciale_expires_on_20251215/chat/completions"
headers = {
"Authorization": f"Bearer {API_KEY}",
"Content-Type": "application/json"
}
# 2. 測試問題
test_questions = [
{
"category": "國際數學奧林匹克(IMO)風格",
"content": "設正整數 a, b, c 滿足 ab + bc + ca = 3。證明:a^2 + b^2 + c^2 + 3abc ≥ 6。請分步驟嚴謹證明。"
},
{
"category": "算法與編程邏輯",
"content": "設計一個算法,判定一個有向圖是否為單連通的(即任意兩點之間至多隻有一條簡單路徑)。請描述思路、給出時間複雜度分析,並用Python實現關鍵部分。"
},
{
"category": "複雜邏輯推理",
"content": "三個邏輯學家走進酒吧,酒保問:'你們三個都要啤酒嗎?' 第一個人説:'我不知道。' 第二個人説:'我也不知道。' 第三個人説:'是的,我們都要啤酒。' 請問最初每個人是否想要啤酒?請還原完整的推理過程。"
}
]
# 3. 發送請求函數
def test_deepseek_speciale(question, max_tokens=4000):
"""向DeepSeek-V3.2-Speciale發送問題並獲取回答"""
payload = {
"model": "deepseek-reasoner", # 使用開啓思考模式的模型名稱
"messages": [
{"role": "system", "content": "你是一個頂尖的數學和邏輯推理專家,請嚴謹、分步驟地思考並解決問題。"},
{"role": "user", "content": question}
],
"thinking": {"type": "enabled"},
"max_tokens": max_tokens,
"stream": False
}
try:
response = requests.post(API_URL, headers=headers, data=json.dumps(payload), timeout=120)
response.raise_for_status()
result = response.json()
# 提取思考過程和最終答案
reasoning_content = result['choices'][0]['message'].get('reasoning_content', '')
final_answer = result['choices'][0]['message']['content']
return reasoning_content, final_answer
except requests.exceptions.RequestException as e:
return f"請求失敗: {e}", ""
except KeyError as e:
return f"響應解析錯誤: {e},原始響應: {response.text}", ""
# 4. 執行測試
if __name__ == "__main__":
print("=" * 60)
print("DeepSeek-V3.2-Speciale 推理能力測試 (思考模式已啓用)")
print("=" * 60)
for i, q in enumerate(test_questions):
print(f"\n測試問題 {i+1} [{q['category']}]:")
print(f"問題: {q['content']}")
print("-" * 40)
reasoning, answer = test_deepseek_speciale(q['content'])
if reasoning:
print(f"\n模型思考過程:\n{reasoning}")
print("-" * 40)
print(f"模型最終答案:\n{answer}")
print("=" * 60)
if i < len(test_questions) - 1:
time.sleep(2) # 避免請求頻率過高
print("\n✅ 所有測試問題已完成!")需要注意的是特別版是收費接口 https://api-docs.deepseek.com/zh-cn/quick_start/pricing。
測試需要通過 https://platform.deepseek.com/ 開通自己的API_KEY。
測試結果截圖如下:
python .\deepseek_python.py
============================================================
DeepSeek-V3.2-Speciale 推理能力測試 (思考模式已啓用)
============================================================
測試問題 1 [國際數學奧林匹克(IMO)風格]:
問題: 設正整數 a, b, c 滿足 ab + bc + ca = 3。證明:a^2 + b^2 + c^2 + 3abc ≥ 6。請分步驟嚴謹證明。
----------------------------------------
模型思考過程:
我們被要求證明:設正整數 a, b, c 滿足 ab + bc + ca = 3,則 a^2 + b^2 + c^2 + 3abc ≥ 6。
注意:a, b, c 是正整數。所以是大於等於1的整數。條件 ab+bc+ca=3。由於是正整數,可能的情況有限制。
我們需要證明不等式 a^2+b^2+c^2+3abc ≥ 6。
由於條件 ab+bc+ca=3,且 a,b,c正整數,可能的組合有哪些?最小的正整數是1,如果全部是1,則ab+bc+ca=1*1+1*1+1*1=3,滿足。所以 (1,1,1) 是一個解。其他可能?假設有一個是2,其他是正整數,則 ab+bc+ca至少?比如 a=2,b=1,c=1 => ab=2, bc=1, ca=2 => sum=5 >3。所以不行。如果 a=2,b=1,c=0? 但0不是正整數。所以只有 (1,1,1) 滿足?還有可能 a=3,b=1,c=0? 不行。也許有 (1,1,1) 是唯一解?但我們需要確認。
設 a,b,c 正整數,ab+bc+ca=3。不妨設 a ≤ b ≤ c。由於 a≥1, b≥1, c≥1。乘積與和。
考慮最小乘積:若 a=1,則條件變為 b + c + bc = 3?實際上 ab+bc+ca = 1*b + b*c + c*1 = b + bc + c = b + c + bc = 3。即 bc + b + c = 3。因式分解 bc + b + c +1 = 4 => (b+1)(c+1)=4。b,c正整數,且 b≤c。則 (b+1)(c+1)=4。可能的分解:1*4, 2*2, 4*1。但 b+1≥2 (因為b≥1 => b+1≥2),c+1≥2。所以可能 (b+1,c+1) = (2,2) 即 b=1,c=1;或 (b+1,c+1) = (1,4) 不可能因為 b+1≥2;或 (4,1) 不可能。所以 b=1,c=1。那麼 a=1。所以 a=b=c=1。如果 a≥2?假設 a≥2,則 b≥a≥2,c≥b≥2。則 ab ≥4, bc≥4, ca≥4,和至少12 >3,不可能。因此唯一的正整數解是 (1,1,1)。所以不等式 a^2+b^2+c^2+3abc ≥ 6 就是 1+1+1+3=6,等號成立。
因此證明是平凡的。但題目可能要求證明對任意正整數滿足條件者成立,但實際只有一種情況。也許 a,b,c 不一定是整數?或者是任意正實數?通常這種不等式是對於正實數條件 ab+bc+ca=3 證明 a^2+b^2+c^2+3abc >=6。可能題目裏 a,b,c 是正實數?再看題目描述:"設正整數 a, b, c 滿足 ab + bc + ca = 3。證明:a^2 + b^2 + c^2 + 3abc ≥ 6。" 既然明確正整數,那就如上述推理,但是也許他們想考察不等式的證明技巧,而不僅僅依賴於窮舉。但窮舉確實證明了,因為只有一組解。然而這種題目出現在不等式證明中,通常是對任意正實數成立,而不僅僅是整數。有可能原題是"正實數"?但這裏寫的是正整數。但即便如此,也可以用基本不等式證明。因為條件 ab+bc+ca=3,我們需要證明 a^2+b^2+c^2+3abc >=6。對於正實數,這個不等式成立嗎?我們來驗證一下:比如取 a=b=1, c=1? 滿足,等號。取 a=b=0.5, c=? 由 ab+bc+ca=0.25+0.5c+0.5c=0.25+c=3 => c=2.75,那麼計算 a^2+b^2+c^2+3abc = 0.25+0.25+7.5625+3*0.5*0.5*2.75=8.0625+3*0.6875=8.0625+2.0625=10.125 >6。似乎成立。對於 a,b,c 不對稱情況呢?比如 a 趨近於 0,則 bc 必須接近 3,但 ab+ac 小,但 bc 大,則 c 和 b 都大,那麼 a^2+b^2+c^2+3abc 會很大。所以可能對正實數成立。但是如果 a,b,c 是正整數,只有 (1,1,1) 這組解,不等式顯然成立(等號)。所以證明是 trivial 的。但既然題目要求嚴謹證明,我們可以先論證正整數的情況只有 (1,1,1),然後直接驗證等號。這是完全嚴謹的。
然而也許題目有誤,應該是正實數。但我們作為AI,需要按照題目給出的條件回答。題目説正整數,我們就按正整數來證明。步驟:
1. 由 a,b,c 是正整數,且 ab+bc+ca=3,推導出 a=b=c=1。
2. 代入不等式左邊得 1+1+1+3=6,等號成立。故不等式成立。
但是,推導 a=b=c=1 的過程需要嚴謹。可以採用如下方法:
- 由於 a,b,c 是正整數,假設 a ≥ b ≥ c(或排序),但最好用對稱性。
- 若 a ≥ 2,則由於 b,c ≥ 1,有 ab ≥ 2*1=2, bc ≥ 1*1=1, ca ≥ 2*1=2,總和至少5>3,矛盾。所以 a ≤ 1。但 a 是正整數,所以 a=1。
- 同理,b 和 c 呢?由對稱性,但注意:當 a=1 時,條件變為 b + c + bc = 3。那麼 b 若 ≥ 2,則 bc ≥ 2c, 且 b + c + bc ≥ 2 + c + 2c = 2 + 3c ≥ 5(因為c≥1),但實際等於3,所以 b 不能≥2。所以 b=1。代入得 1 + c + 1*c = 1 + c + c = 1+2c=3 => c=1。所以 a=b=c=1。
但更直接:由對稱性,我們可證任何一個變量都只能為1。所以只有一組解。
因此,證明完成。
但是,也許出題人希望用不等式方法,比如 Schur 不等式等,因為原不等式與 Schur 有關。但是針對正整數,太簡單了。不過既然問題明確要求"請分步驟嚴謹證明",我們應提供完整推理。
我們可以給出兩種證明:一種基於正整數分類,一種基於一般正實數(如果不限制整數)。但題目明確正整數,所以應該使用前者。不過,可能需要考慮到當 a,b,c 都是正整數時,ab+bc+ca=3 只有一組解,所以不等式自動成立。這確實是一個嚴謹的證明。
但這樣證明可能顯得過於簡單,也許他們認為正整數範圍也包括其他解?讓我們再仔細考慮一下:正整數包括 1,2,3,... 那麼是否有 a=3,b=1,c=0? 0 不是正整數。所以沒有。也許 a=2,b=1,c=? 求解方程:2*1+1*c+2*c = 2 + c + 2c = 2+3c =3 => 3c=1 => c=1/3 不是整數。所以不行。 a=3,b=1: 3*1+1*c+3*c = 3 + c+3c = 3+4c=3 => 4c=0 => c=0,不行。所以確實只有 (1,1,1)。
還可以考慮 a=1,b=2,c? 1*2+2*c+1*c = 2+2c+c=2+3c=3 => 3c=1 => c=1/3 不行。
所以唯一。
因此,證明完成。
我們還可以使用不等式方法:比如由均值不等式等推導出 a^2+b^2+c^2 ≥ ab+bc+ca = 3,所以左邊 ≥ 3+3abc。還需要證明 3abc ≥ 3 => abc ≥ 1。但由 ab+bc+ca=3 和正整數條件,可以推出 abc≥1?對於正實數不一定,比如 a=b=0.5,c=2.75,abc=0.5*0.5*2.75=0.6875<1。所以不等式 3+3abc ≥ 6 即 abc ≥ 1 不一定成立。所以需要更精細的不等式。
但既然我們針對正整數,已經得到了唯一解,無需複雜。
那麼,我們就按照正整數情況證明。在回答中,我們可以先説明由條件 ab+bc+ca=3 和正整數性質,可以推出 a=b=c=1。過程如下:
步驟1: 假設 a,b,c 是正整數,且 ab+bc+ca=3。
步驟2: 注意到對於正整數,如果有一個大於等於2,則... 證明 a ≤ 1, b ≤ 1, c ≤ 1,但正整數所以為1。
詳細:若 a ≥ 2,由於 b,c ≥ 1,則 ab ≥ 2, bc ≥ 1, ca ≥ 2,總和 ≥ 5 > 3,矛盾。故 a ≤ 1,因此 a=1。
步驟3: 代入 a=1 得 1·b + b·c + c·1 = b + bc + c = 3 => (b+1)(c+1) = 4。
步驟4: 由於 b,c 是正整數,解 (b+1)(c+1)=4 得 b=c=1。
步驟5: 因此 a=b=c=1。
步驟6: 代入不等式左邊:1^2+1^2+1^2+3*1*1*1 = 6,故不等式成立,等號成立。
這就是完整證明。
但是,有沒有可能 a,b,c 不排序導致上述推理不夠嚴密?我們説"若 a ≥ 2" 是可行的,因為對稱性,可以任意選一個變量。更嚴格地説:由於對稱性,我們可以假設 a 是最大的或最小的?但是不用,直接説:假設 a ≥ 2,則因為 b,c ≥ 1,得到矛盾,所以 a ≤ 1,即 a=1。然後同樣地,得到 b=1,c=1。這是正確的。
因此,我們給出證明。
然而,有的競賽題可能會出這樣的不等式,但條件 ab+bc+ca=3 和 a,b,c 正整數,結論 a^2+b^2+c^2+3abc ≥ 6,這確實是 trivial 的。但是有時候他們會要求證明對任意實數滿足該條件成立?但題目寫正整數,我們按照題目做。
也許這是題目的一個 trick,讓你意識到只有一種可能,從而簡化證明。
所以最終答案就是上述步驟。
但為了更顯完整,我們可以補充:當 a,b,c 是正整數時,由條件可知它們只能是 1,因此不等式變為等式,成立。
我們按要求分步驟,嚴謹證明。
下面給出最終回答。
----------------------------------------
模型最終答案:
**證明**
設正整數 \(a, b, c\) 滿足 \(ab + bc + ca = 3\)。
**步驟 1** 證明 \(a = 1\)。
反設 \(a \ge 2\)。因為 \(b, c\) 為正整數,故 \(b \ge 1,\ c \ge 1\)。此時
\[
ab \ge 2,\quad bc \ge 1,\quad ca \ge 2,
\]
從而
\[
ab + bc + ca \ge 2 + 1 + 2 = 5 > 3,
\]
與已知條件矛盾。因此 \(a \le 1\),又 \(a\) 為正整數,所以 \(a = 1\)。
**步驟 2** 代入 \(a = 1\),條件化為
\[
1 \cdot b + b \cdot c + c \cdot 1 = b + bc + c = 3.
\]
將等式兩邊加 1:
\[
(b + bc + c) + 1 = 4 \quad\Longrightarrow\quad (b + 1)(c + 1) = 4.
\]
**步驟 3** 解 \((b+1)(c+1) = 4\)。
因為 \(b, c\) 為正整數,故 \(b+1 \ge 2,\ c+1 \ge 2\)。\(4\) 在正整數範圍內的因子組合只有
\[
(b+1,\ c+1) = (2,2) \quad\text{或}\quad (1,4),\ (4,1),
\]
後兩組不滿足最小值要求。因此必有 \(b+1 = c+1 = 2\),從而
\[
b = 1,\quad c = 1.
\]
**步驟 4** 所以
\[
a = b = c = 1.
\]
**步驟 5** 代入不等式左邊:
\[
a^2 + b^2 + c^2 + 3abc = 1^2 + 1^2 + 1^2 + 3 \cdot 1 \cdot 1 \cdot 1 = 1 + 1 + 1 + 3 = 6.
\]
因此
\[
a^2 + b^2 + c^2 + 3abc \ge 6,
\]
等號成立。
綜上,原不等式得證。
============================================================
測試問題 2 [算法與編程邏輯]:
問題: 設計一個算法,判定一個有向圖是否為單連通的(即任意兩點之間至多隻有一條簡單路徑)。請描述思路、給出時間複雜度分析,並用Python實現關鍵部分。
----------------------------------------
模型思考過程:
我們被要求設計一個算法,判定一個有向圖是否為單連通的,即任意兩點之間至多隻有一條簡單路徑。注意定義:單連通 (singly connected) 或 "uniquely connected"? 通常在圖論中,有向圖的單連通性 (singly connected) 意味着對於任意兩個頂點 u 和 v,從 u 到 v 至多存在一條簡單路徑(即路徑上頂點不重複)。注意這是針對有向圖的。這個概念和強連通性不同。在有些文獻中,單連通圖也稱為 "有向無環圖"? 不一定,因為有環圖也可能滿足任意兩點之間至多隻有一條簡單路徑嗎?如果存在環,則可能有兩個不同簡單路徑?例如 u->v 有直接邊,也有通過其他節點的路徑,則可能會有兩條簡單路徑。但是環本身可能產生兩條路徑?假設有向圖:1->2, 2->1 這個環,那麼從1到2有兩條簡單路徑:直接邊,和1->2->1->2? 注意簡單路徑不允許重複頂點,所以1->2->1->2不是簡單路徑因為重複了頂點1和2。從1到2的簡單路徑有哪些?直接1->2是一條;還有1->2->1->2不是簡單;1->2->1? 那是從1到1。所以從1到2只有一條簡單路徑。但可以從1->2(直接),還有1->? 如果沒有其他路徑,那就只有一條。但是考慮有向環:1->2, 2->3, 3->1。那麼從1到2:直接1->2;另一條1->2? 1->3->1->2? 不是簡單;1->3->1? 不是到2;1->2->3->1->2? 重複。也許我們無法得到第二條簡單路徑,因為任何環都會導致路徑繞圈,但簡單路徑不能重複頂點。所以有環圖也可能滿足任意兩點之間至多隻有一條簡單路徑。但實際上,如果圖中有向環,可能會產生兩條不同的簡單路徑?考慮一個有向環: 1->2, 2->3, 3->1。從1到3的路徑:直接? 沒有直接邊;1->2->3是一條;還有1->2->3->1->2->3? 重複。所以只有一條。似乎有向環並不一定產生兩條簡單路徑。但如果有一個頂點有多條出邊,可能產生多條路徑。例如:1->2, 1->3, 3->2。則從1到2有兩條簡單路徑:1->2 和 1->3->2。所以該圖不是單連通的。
因此,問題歸結為判斷一個有向圖是否滿足:對於任意兩個頂點 u, v,從 u 到 v 的簡單路徑至多一條。
這是圖論中的一個經典問題:Singly connected directed graph。可以通過對每個頂點進行深度優先搜索 (DFS) 並檢查是否在 DFS 樹中發現後向邊(back edge)或交叉邊?但注意簡單路徑的數量限制。實際上,如果存在兩個不同的簡單路徑從 u 到 v,那麼圖中必然包含一個從 u 到 v 的有向路徑,以及另一條不相交(或部分重疊)的路徑。這可能意味着圖中包含一個點或邊,使得存在兩條路徑到達同一個點。
一種直接的算法是對每對頂點檢查是否有多條路徑。但這樣太慢。我們需要高效算法。
回想有向圖的單連通性判定。我記得有一個結論:一個有向圖是單連通的當且僅當它的反圖(transpose)也是單連通的?不一定。
考慮使用 DFS 的算法:對每個頂點 s 進行 DFS,如果在 DFS 過程中發現從 s 開始的 DFS 樹中,某個節點 v 被訪問時存在另一條從 s 到 v 的路徑(即發現 v 已經在當前 DFS 棧中?或者是發現了橫叉邊或前向邊?)實際上,如果存在兩條不同的簡單路徑從 s 到 v,那麼 DFS 從 s 開始探索時,可能會在發現 v 之後,又通過另一條邊到達 v。在 DFS 中,當我們遇到一個已經訪問過的節點時,根據邊的類型可以判斷。但關鍵是:我們如何檢測是否存在從起始點 s 到某個節點 v 的多條簡單路徑?
如果我們進行深度優先搜索,並維護每個節點的 discovery/finish 時間(時間戳)。在 DFS 過程中,當遇到一條邊 (u, v) 時:
- 如果 v 未被訪問,則是樹邊。
- 如果 v 已訪問但未完成(即在遞歸棧中),則是後向邊,表示存在有向環。
- 如果 v 已訪問且已完成,則是前向邊或交叉邊(取決於時間戳)。前向邊是從祖先指向後代(在 DFS 樹中),交叉邊是指向其他已完成的子樹。
現在,如果在從 s 開始的 DFS 中,存在兩條不同的簡單路徑從 s 到 v,這意味着什麼?意味着在 DFS 樹中,v 被第一次訪問通過一條路徑(樹邊)。如果存在另一條路徑,那麼在 DFS 探索過程中,當沿着另一條路徑的某個邊到達 v 時,v 可能已經被訪問過。此時,這條邊可能是前向邊或交叉邊(或後向邊,但後向邊指向祖先,所以從 s 到 v 的後向邊不可能,因為 s 是根,v 是後代,後向邊只能從後代指向祖先,所以不會從祖先到後代)。對於從 s 開始的 DFS,任何從 s 出發的路徑最終到達 v,如果 v 已經被訪問,那麼邊 (x, v) 可能是前向邊(如果 v 是 x 的後代)或交叉邊(如果 v 在另一棵已完成的子樹中)。但這兩種邊都可能指示存在另一條從 s 到 v 的路徑?讓我們分析。
情形1:前向邊 (x, v)。在 DFS 樹中,v 是 x 的後代,這意味着已經存在一條從 x 到 v 的樹路徑。加上邊 (x, v),則從 x 到 v 有兩條不同的簡單路徑:一條是樹路徑(經過中間節點),另一條是直接邊。那麼從 s 到 v 呢?如果 s 是根,從 s 到 v 的路徑:s -> ... -> x -> ... -> v(樹路徑)和 s -> ... -> x -> v(通過前向邊)實際上是兩條不同的路徑,因為前者經過樹路徑從 x 到 v,後者經過直接邊。但這兩條路徑都經過 s 到 x 部分,如果 s 到 x 的部分相同,那麼從 s 到 v 的整個路徑只是從 x 開始分叉,仍然是兩條不同的簡單路徑,因為從 x 到 v 的部分不同。所以存在前向邊就會產生從 s 到 v 的多條簡單路徑?注意:前向邊是從祖先指向後代,但 s 是根,所以 x 是 s 的後代。從 s 到 v 的兩條路徑:一條是樹路徑(s 到 x 的樹路徑 + 從 x 到 v 的樹路徑),另一條是 s 到 x 的樹路徑 + 直接邊 (x, v)。這兩條路徑是不同的,因為從 x 到 v 的部分不同。因此,存在從某個節點 x 到其後代 v 的前向邊,則從根 s 到 v 至少有兩條簡單路徑。但如果前向邊是從 s 直接指向 v(即 s 是根),而樹路徑也經過其他節點,那麼也是兩條路徑。所以,在 DFS 中如果發現前向邊,就可能意味着存在多條路徑。但是否總是?考慮這樣的圖:s->a, a->b, b->v, 還有一條邊 s->v。DFS 從 s 開始,先走 s->a,然後 a->b, b->v,訪問 v。之後回退,當探索 s 的其他鄰接邊時發現 s->v,此時 v 已經完成訪問,且 v 的發現時間晚於 s,所以邊 (s, v) 是一條前向邊。這就導致了從 s 到 v 的兩條路徑:s->a->b->v 和 s->v。所以的確不是單連通。
情形2:交叉邊 (x, v)。在 DFS 樹中,v 不屬於 x 的後代,且 v 已經完成訪問。這意味着 v 的訪問和完成都比 x 早(因為交叉邊一般是從發現時間晚的節點指向發現時間早的節點)。但交叉邊也可能是從 s 的 DFS 樹中的一個節點指向另一棵已經完成的子樹(可能是之前的起點)。但因為我們是從 s 開始 DFS,所以所有節點都應該是從 s 可達的,否則 v 不可達?如果 v 從 s 不可達,那麼我們從 s 開始 DFS 不會訪問到 v,所以不考慮。但是,如果從 s 可達 v,並且存在交叉邊 (x, v),那麼 v 在 DFS 樹中的發現時間可能早於 x,但 v 是 x 的後代?如果 v 不是 x 的後代但 v 已被訪問且完成,那麼意味着 v 的 DFS 子樹已經完成。存在交叉邊 (x, v) 可能指示存在另一條路徑?考慮一個圖:s->a, s->b, a->v, b->v。從 s 開始 DFS,假設先走 s->a,然後 a->v 訪問 v,完成 v 後回溯,然後從 s 探索 s->b,當探索 b->v 時,v 已經完成,且 v 的發現時間早於 b 的發現時間(因為 b 是在 a 之後才發現的?實際上 DFS 從 s 開始,訪問 a,然後 v,然後回溯到 s,再訪問 b。所以當發現邊 b->v 時,v 已經完成,且 v 不是 b 的後代(因為 b 在另一分支),所以 b->v 是一條交叉邊。這種情況下,從 s 到 v 有兩條路徑:s->a->v 和 s->b->v。所以交叉邊也導致多條路徑。
但是,是否所有多條路徑的情況都會在 DFS 中發現前向邊或交叉邊?考慮存在兩條路徑但它們在某個點之後合併,而 DFS 樹中可能會將其中一條作為樹路徑,另一條中的某些邊可能成為後向邊嗎?後向邊是從後代指向祖先,對於從 s 到 v 的路徑,如果另一條路徑是 s->...->x->...->v,其中 x 是某個節點,但另一條路徑可能先走到 v 的祖先,然後通過後向邊往下?比如圖:s->a, a->b, b->c, c->a(環),還有一條 s->c。從 s 到 c 的路徑:s->a->b->c 和 s->c。DFS 從 s 開始,可能先走 s->a,然後 a->b, b->c 訪問 c,完成 c 後回溯,然後探索 s->c,發現 c 已完成且發現時間晚於 s?c 的發現時間晚於 s,但是 c 已經完成,且 c 不是 s 的後代?c 是 s 的後代,因為是通過 a,b 到達的,所以 s->c 是一條前向邊。因此被檢測到。
另一個複雜情況:可能存在兩條路徑共享部分前綴,但在某個點分叉後又匯合。在 DFS 中,如果我們將其中一條作為樹邊,另一條中的邊可能會被標記為前向邊或交叉邊,具體取決於遍歷順序。
因此,直覺上,對於從一個源點 s 開始的 DFS,如果存在兩個不同的簡單路徑從 s 到某個節點 v,那麼在 DFS 中必然存在一條非樹邊(前向邊或交叉邊)指向 v 或者指向 v 的某個祖先?等等,考慮兩條路徑:s->a->b->d 和 s->a->c->d。這裏 a 是共同前綴。DFS 從 s 開始,先走 s->a,然後從 a 選擇一條邊,比如 a->b,然後 b->d 訪問 d。當回溯到 a 後,探索 a->c,然後 c->d,此時 d 已經被訪問過。d 是 a 的後代嗎?在 DFS 樹中,d 是 b 的後代,而 b 是 a 的後代,所以 d 也是 a 的後代。因此,邊 c->d:c 是從 a 剛探索的,d 已經是訪問過且已完成?取決於 d 是否已完成。如果 d 在 b 的子樹中已經完成,那麼 c->d 是一條從 a 的後代 c 指向另一後代 d 的邊,這種邊被稱為橫跨邊?在 DFS 中,如果 d 的完成時間比 c 的發現時間早?實際上,當我們從 a 開始探索 c 時,d 可能已經完成(因為在 b 的子樹中先完成了)。因為 d 是 b 的後代,b 完成後 d 才完成。b 的完成可能在探索 c 之前。所以 c 的發現時間晚於 d 的完成時間?考慮時間線:從 s 開始,發現 s,發現 a(作為 s 的孩子),然後從 a 探索 b,發現 b,發現 d(通過 b),然後完成 d,完成 b,回溯到 a,此時 a 還未完成,然後探索 c,發現 c,然後探索 c->d,此時 d 已經完成,且 d 的發現時間晚於 a 但早於 c?實際上,d 的發現時間是在 b 之後,c 的發現時間是在 b 完成後,所以 d 的發現時間早於 c 的發現時間。並且 d 不是 c 的後代(c 剛被發現),所以邊 c->d 是一條從較晚發現的節點 c 指向較早發現的節點 d 的邊,且 d 不在 c 的子樹中(因為 c 的子樹還沒開始),所以這是一條交叉邊。所以這種也被檢測為交叉邊。
但是,考慮兩條路徑完全不相交(除起點終點)的情況:s->a->v 和 s->b->v。如前所述,交叉邊。
因此,從源點 s 開始的 DFS,如果存在另一條從 s 到 v 的簡單路徑,那麼在 DFS 中必然存在一條非樹邊指向 v(可能前向邊或交叉邊)。這是正確的嗎?還需要考慮可能通過後向邊間接產生第二條路徑?例如 s->a, a->b, b->a(環),s->b。從 s 到 b 的兩條路徑:s->a->b 和 s->b。在 DFS 中,先探索 s->a,然後 a->b,訪問 b,然後 b->a 是一條後向邊(指向祖先 a)。但邊 s->b 可能是前向邊或交叉邊,取決於順序。如果我們在探索完 b 的子樹後才處理 s->b,那麼 s->b 是前向邊(因為 b 是 s 的後代)。所以仍然檢測到非樹邊指向 b。
如果第二條路徑涉及環,比如 s->a, a->b, b->c, c->b,從 s 到 b 的路徑:s->a->b 和 s->a->b->c->b?但第二條路徑不是簡單路徑,因為重複頂點 b 和 c?簡單路徑不允許重複頂點,所以 s->a->b->c->b 不是簡單路徑。所以不考慮。
因此,似乎對於從固定源點 s,檢測是否存在從 s 到任意 v 的多條簡單路徑,可以通過執行一次 DFS,並檢查是否存在非樹邊指向一個已經被訪問過的節點,且該節點可以從 s 通過另一條路徑到達?但問題是我們需要確保這條非樹邊實際上提供了另一條從 s 到 v 的路徑。但任何非樹邊 (u, v) 如果在 DFS 過程中遇到,並且 v 已經被訪問過,且從 s 到 u 是可達的(顯然,因為 u 是在 DFS 中被訪問的),那麼從 s 到 v 就存在兩條路徑:一條是 DFS 樹中 s 到 v 的路徑(樹路徑),另一條是 s 到 u 的樹路徑加上邊 (u, v)。但問題是,樹路徑 s 到 v 存在嗎?由於 v 已經被訪問,並且是在當前 DFS 樹中,那麼從 s 到 v 有一條樹路徑(因為 v 是第一次被訪問時通過樹邊到達的)。如果 v 是在當前 DFS 中通過樹邊第一次訪問的,那麼樹路徑存在。但注意:v 可能不是從 s 可達的?但如果 v 被訪問了,它一定是從 s 可達的,因為 DFS 從 s 開始。所以 v 必然是從 s 可達的,且有一條樹路徑。那麼邊 (u, v) 提供了一個替代路徑,只要這條路徑不同於樹路徑。是否可能 (u, v) 提供的路徑與樹路徑相同?如果 (u, v) 本身就是樹邊?但樹邊只會在 v 未被訪問時走。如果 v 已訪問,那麼 (u, v) 是非樹邊。如果 (u, v) 是前向邊,並且 v 是 u 的後代,那麼 s->...->u(樹路徑)加上 (u, v) 與 s->...->u->...->v(樹路徑)不同,因為後者經過 u 的後代路徑,前者直接跳。所以不同。如果是交叉邊,v 不是 u 的後代,但 s 到 v 的樹路徑存在,這兩條路徑也不同,因為從 u 出發的路徑不經過 v 在樹中的父節點,路徑序列不同。但是否可能 (u, v) 提供的路徑和樹路徑實際上是同一條?例如,如果 v 是 u 的直接子節點(在樹中),但 (u, v) 也被標記為前向邊?如果 v 是 u 的直接子節點,那麼 (u, v) 應該是樹邊,不會成為前向邊,因為當第一次訪問 v 時是通過 (u, v) 樹邊。之後不會再遇到 (u, v) 因為邊已經遍歷過了?但在圖表示中,鄰接表裏可能有多條相同的邊?簡單圖不允許重邊,但可能有兩個不同的邊?如果有重邊
----------------------------------------
模型最終答案:
============================================================
測試問題 3 [複雜邏輯推理]:
問題: 三個邏輯學家走進酒吧,酒保問:'你們三個都要啤酒嗎?' 第一個人説:'我不知道。' 第二個人説:'我也不知道。' 第三個人説:'是的,我們都要啤酒。' 請問最初每個人是否想要啤酒?請還原完整的推理過程。
----------------------------------------
模型思考過程:
我們面臨一個經典邏輯謎題。三個邏輯學家走進酒吧,酒保問:"你們三個都要啤酒嗎?" 第一個人説:"我不知道。" 第二個人説:"我也不知道。" 第三個人説:"是的,我們都要啤酒。" 我們需要推斷最初每個人是否想要啤酒。假設每個邏輯學家都知道自己想要啤酒與否,並且他們知道其他人都是邏輯學家,且都誠實且完美推理。他們聽到前面的人的回答後進行推理。酒保的問題是“你們三個都要啤酒嗎?”意思是問是否三個人都想要啤酒。每個人根據自己的知識和聽到的回答回答“是”或“否”或“我不知道”。他們只説真話,而且只有在確知答案時才給出確定回答,否則説“我不知道”。
我們需要推斷每個人的意願(是否想要啤酒)。通常這類問題通過逆向推理。每個人都是完美的邏輯學家,他們會根據已知信息(自己的意願和前面人的回答)判斷是否可以確定三人是否都要啤酒。
設A、B、C分別表示第一個人、第二個人、第三個人的意願:1表示想要啤酒,0表示不想要。
問題:三人是否都要啤酒?即命題P = (A=1 and B=1 and C=1)。他們回答的是對這個命題的真假的確定性。
第一人:聽到問題後,他知道自己的意願A,但不知道B和C。他回答“我不知道”,這意味着他無法確定P是否為真。如果他知道P一定為假(即不可能三人全要),他會回答“否”;如果他知道P一定為真,他會回答“是”。他説“我不知道”,説明他既不能肯定P為真,也不能肯定P為假。這意味着根據他知道的A以及他知道B和C未知,P可能是真也可能是假。但關鍵在於:他只能基於自己的意願來推斷。如果A=0,那麼P顯然是假的(因為三人全需要每個人都是1,有一個0則假),所以如果A=0,他就可以確定答案為“否”,他就會回答“否”。但是他説“我不知道”,因此A不可能是0,否則他應回答“否”。所以A必須為1。而且,即使A=1,他還不知道B和C,P的真假取決於B和C。所以如果A=1,那麼存在B和C的可能組合使得P為真(B=1,C=1)和P為假(其他情況),因此他不能確定,所以會説“我不知道”。這符合。
因此推理:第一個人説不知道 ⇒ A = 1。
第二個人:他聽到第一個人的回答,並且知道自己的意願B,但不知道C。他也知道第一個人是邏輯學家,會根據A作出回答。現在第二個人需要基於已知信息:他知道A=1(因為第一個人回答“我不知道”意味着A=1,第二個人可以推斷出這一點,因為他知道第一個人是理性的)。實際上第二個人聽到第一個人説不知道,他可以推斷出A=1。此外,他知道自己的意願B。然後他回答“我也不知道”。這意味着他無法確定P的真假(即三人全要)。他回答“我不知道”意味着,給定他所知道的(A=1,B,以及他還沒聽到C的回答),P的真假不是確定的。也就是存在一些可能的情況(C的可能取值)使得P為真,也存在另一些使得P為假,且這些可能性都與當前信息一致(包括前一個人的回答的推理)。此外,他還要考慮第一個人回答的合理性。
我們需要判斷第二個人在什麼情況下會回答“是”或“否”或“我不知道”。如果他能確定P為真,則回答“是”;如果能確定P為假,則回答“否”;否則“我不知道”。
第二個人已知:A=1(從第一個回答推斷),B已知(他自己的意願),但C未知。那麼P = (1 & B & C) = B & C。因為A=1,所以P為真當且僅當B=1且C=1。
如果B=0,那麼P = 0不管C是什麼。此時第二個人可以確定P為假,就會回答“否”。但他回答“我不知道”,所以B不能是0。因為如果B=0,他肯定回答“否”。所以B必須為1。
如果B=1,那麼P = C。因此P的真假完全取決於C。由於C未知(第三個人的意願未知),第二個人無法確定P的真假,所以他會回答“我不知道”。但要注意:第二個人是否還有額外信息?他聽到第一個人説“我不知道”,他知道第一個人推理出A=1,但這是已知的。沒有更多了。所以如果B=1,他會説“我不知道”。這符合他回答“我不知道”。所以從第二個人説“我不知道”推斷B=1。
但有沒有可能B=0而第二個人由於某些其他原因仍説“我不知道”?假設B=0,那麼P肯定是假。但是否有其他限制使得第二個人不能確定?因為P是“三人全要”,如果B=0,則至少有一人不想要,所以P假。那麼第二個人就可以肯定地回答“否”。所以他會説“否”。但是他實際説“我不知道”,因此B不可能為0。所以B=1。
因此第二個人説不知道 ⇒ B = 1。
注意:這裏還隱含了第二個人知道第一個人是理性的,且第一個人的回答已經推導出A=1。但即使第一個人非理性,但題目説他們是邏輯學家,所以我們可以這樣推。
第三個人:他聽到前兩個人的回答,他知道前兩個人都是邏輯學家,並且他們分別説了“我不知道”。第三個人知道自己的意願C。此外,他從第一個人的回答推斷A=1;從第二個人的回答(基於A=1)推斷B=1。因為第二個人説“我不知道”且A=1推斷B=1。第三個人是完美的,所以他能推斷出A=1,B=1。現在他知道C。那麼P = A & B & C = 1 & 1 & C = C。所以P的真假取決於C。如果C=1,則P為真;如果C=0,則P為假。第三個人能夠確定P的真假,因為他知道C。所以他會回答“是”或“否”確定地。但實際上第三個人回答“是的,我們都要啤酒。”這意味着他説“是”,即P為真。所以C=1。
因此結論:A=1, B=1, C=1,三個人都想要啤酒。
這個推理是經典的。
但題目問:“請問最初每個人是否想要啤酒?”所以答案是都想要。
但需要完整還原推理過程。
還有一點細節:在第二個人推理時,他必須考慮到第一個人説“我不知道”這個事實,並且他知道第一個人是理性的。但我們已經用了。不過需要注意第二個人是否可能推斷出第一個人是理性但還有其他可能性?例如,如果第一個人是理性的,他只有在A=1時説不知道。所以可以推出A=1。如果第二個人考慮第一個人可能非理性,但題目假設都是邏輯學家,所以我們確定。
因此最終答案:三個人最初都想要啤酒。
推理過程分步驟:
1. 第一個人的回答分析:如果他不想要,他知道至少一人不要,即可確定答案“否”,但他回答“我不知道”,所以他必然想要啤酒(A=1)。
2. 第二個人聽到第一個人的回答,推斷出A=1。如果他不想要,則知道三人不全要,可回答“否”。但他回答“我不知道”,所以他也想要啤酒(B=1)。
3. 第三個人聽到前兩人的回答,推斷出A=1和B=1。他自己知道自己是否想要。如果他想要,則三人全要,回答“是”;如果不想要,則回答“否”。他回答“是”,所以他也想要(C=1)。
因此三人都要啤酒。
這就是完整的推理。
注意:有些變體問題可能問是否還有其他可能,但標準解答就是三人都要。
所以最終輸出答案。
----------------------------------------
模型最終答案:
根據問題描述,三個邏輯學家都是完美理性的,他們知道自己的意願,並基於已有信息進行推理。酒保問:“你們三個都要啤酒嗎?”即詢問三人是否都想要啤酒。回答規則:只有在確知答案時才會給出肯定或否定的回答,否則説“我不知道”。
**推理過程:**
- **第一個人**
他知道自己的意願(設為 A)。
- 如果 A = 0(他不想要),則三人不可能都要,因此他能確定答案為“否”。
- 如果 A = 1(他想要),則答案取決於另兩人,他無法確定。
他説“我不知道”,因此他不能確定答案,由此推出 A 不可能為 0,故 **A = 1**(他想要啤酒)。
- **第二個人**
他聽到第一個人的回答,並知道第一個人是理性的,因此推斷出 A = 1。
他知道自己的意願(設為 B)。此時已知 A = 1,三人全要的條件變為 B = 1 且 C = 1。
- 如果 B = 0,則無論如何 C 為何值,三人都不可能都要,他能確定答案為“否”。
- 如果 B = 1,則答案取決於 C,他無法確定。
他説“我也不知道”,因此他不能確定答案,故 B 不可能為 0,所以 **B = 1**(他想要啤酒)。
- **第三個人**
他聽到前兩人的回答,並知道他們都是理性的,因此推斷出 A = 1 且 B = 1。
他知道自己的意願(設為 C)。此時三人全要的條件變為 C = 1。
他能夠確定答案:若 C = 1 則答案為“是”,若 C = 0 則答案為“否”。
他回答“是的,我們都要啤酒”,因此 **C = 1**(他想要啤酒)。
**結論:** 最初三個人都想要啤酒。
============================================================
✅ 所有測試問題已完成!本次測試我共向模型拋出 3 道題目,過程中發現一個有趣的現象:第二題的回覆僅完整呈現了推理鏈路,卻未給出最終結論。更值得一提的是,整個測試過程的 API 調用成本不到 3 分錢,性價比相當突出。
出於對「缺失最終答案」這一情況發生概率的好奇,我緊接着用相同代碼重新運行了一次測試。沒想到這次的結果更具代表性 —— 第一題和第二題的回覆均只保留了詳細的思考過程,最終答案依舊「缺席」。從這兩次測試的結果來看,這款 Speciale 特別版模型目前在輸出完整性上仍有優化空間,確實還存在一定的不成熟之處。
============================================================
DeepSeek-V3.2-Speciale 推理能力測試 (思考模式已啓用)
============================================================
測試問題 1 [國際數學奧林匹克(IMO)風格]:
問題: 設正整數 a, b, c 滿足 ab + bc + ca = 3。證明:a^2 + b^2 + c^2 + 3abc ≥ 6。請分步驟嚴謹證明。
----------------------------------------
模型思考過程:
我們要證明對於正整數 a, b, c 滿足 ab+bc+ca=3,有 a^2+b^2+c^2+3abc ≥ 6。
首先,a,b,c 是正整數,即自然數 1,2,3,...,但題目中可能允許 0?正整數通常是從1開始的自然數,但有時0不是正整數。我們這裏取正整數就是自然數 ≥1。
已知 ab+bc+ca=3,且 a,b,c 是正整數。我們考慮可能的三元組。
由於 a,b,c 都是正整數,ab+bc+ca=3 是一個相當小的數。因為如果有一個數大於等於2,則與其他數的乘積至少為? 我們分析可能的取值。
設 a,b,c ≥ 1,則 ab ≥ 1, bc ≥ 1, ca ≥ 1,所以 ab+bc+ca ≥ 3。已知等於3,因此必須有 ab=bc=ca=1,即每對乘積都為1。這隻有在 a=b=c=1 時成立,因為如果 a=1,b=1,c=1,則 ab=1, bc=1, ca=1。若 a=1,b=1,c=2,則 ab=1, ac=2, bc=2 和為5 >3。所以唯一可能正整數解是 (1,1,1)。但檢查 a,b,c 都是正整數,乘積和為3,但最小和確實是3,當 a=b=c=1 時成立。那其他組合呢?比如 a=1,b=2,c=? 則 ab=2, ac=c, bc=2c。和為2 + c + 2c = 2+3c = 3 => 3c=1 => c=1/3 不是整數。所以唯一正整數解是 (1,1,1)。那麼不等式 a^2+b^2+c^2+3abc ≥ 6 在 (1,1,1) 時:1+1+1+3=6,等號成立。所以不等式成立且取等。命題就顯然了。
但問題是,題目説正整數,是不是可能包括0?通常正整數就是自然數(1,2,3,...)。如果是非負整數(包括0)那麼可能有其他解。但題目明確説正整數,所以唯一解就是1,1,1。這時不等式等號成立。證明完畢?但似乎太簡單了。也許題目本意是 a,b,c 是非負實數?或者 a,b,c 是正實數?但題目寫的是正整數。可能是印刷問題,很多不等式題目是“正實數”滿足 ab+bc+ca=3,證明 a^2+b^2+c^2+3abc ≥ 6。我認為這是更常見的類型:對於正實數 a,b,c 滿足 ab+bc+ca=3,證明 a^2+b^2+c^2+3abc ≥ 6。因為如果限制為正整數,證明就沒什麼意思了。鑑於題目要求“分步驟嚴謹證明”,很可能是正實數。但題目寫的是正整數,可能是誤寫。我們再看:若 a,b,c 是正實數,條件 ab+bc+ca=3,結論 a^2+b^2+c^2+3abc ≥ 6。這是常見的代數不等式。我們可以嘗試證明。
我們需要證明:對於正實數 a,b,c 滿足 ab+bc+ca=3,有 a^2+b^2+c^2+3abc ≥ 6。
這看起來像是一個Schur不等式或者用已知不等式轉化。觀察形式: a^2+b^2+c^2 和 ab+bc+ca 的關係,加上 3abc。已知 ab+bc+ca=3,目標要 >=6。我們可以嘗試利用已知不等式:a^2+b^2+c^2 ≥ ab+bc+ca =3(當 a=b=c=1時取等)。那麼 a^2+b^2+c^2+3abc ≥ 3+3abc。要證 ≥6,即需 3abc ≥3,即 abc ≥1。但 abc 是否一定 ≥1?對於正實數 a,b,c 滿足 ab+bc+ca=3,abc 可以小於1?例如 a=0.5,b=0.5,c=... 我們解一下:設 a=b=0.5,則 ab=0.25,ac=0.5c,bc=0.5c,所以 0.25 + c =3 => c=2.75,abc=0.5*0.5*2.75=0.6875<1。所以 abc 可能小於1。因此單純用 a^2+b^2+c^2 ≥ 3 不夠。
我們需要更強的估計。
我們可以考慮使用不等式 a^2+b^2+c^2+3abc ≥ 2(ab+bc+ca) 或類似?實際上如果 a=b=c=1,兩邊都是6。嘗試證明 a^2+b^2+c^2+3abc ≥ 2(ab+bc+ca)。因為已知 ab+bc+ca=3,那麼右邊就是6。所以就是要證 a^2+b^2+c^2+3abc ≥ 2(ab+bc+ca),即 a^2+b^2+c^2+3abc - 2(ab+bc+ca) ≥ 0。這個式子可以因式分解?考慮 Schur 不等式:對於任意非負實數 a,b,c,有 a^3+b^3+c^3+3abc ≥ a^2(b+c)+b^2(c+a)+c^2(a+b),即 Σ a^3 +3abc ≥ Σ a^2(b+c)。但我們的式子是關於平方和和對稱和。我們可以將 a^2+b^2+c^2 寫成 Σ a^2。考慮移項: Σ a^2 +3abc - 2Σ ab = Σ a^2 - 2Σ ab +3abc = (a+b+c)^2 - 4(ab+bc+ca) + 3abc? 因為 (a+b+c)^2 = Σ a^2 + 2Σ ab,所以 Σ a^2 - 2Σ ab = (a+b+c)^2 - 4Σ ab。所以原不等式等價於 (a+b+c)^2 - 4Σ ab + 3abc ≥ 0,即 (a+b+c)^2 - 4(ab+bc+ca) + 3abc ≥ 0。由於 Σ ab = 3,所以即 (a+b+c)^2 - 12 + 3abc ≥ 0,即 (a+b+c)^2 + 3abc ≥ 12。但這更強?實際上我們需要 (a+b+c)^2 ≥? 並不顯然。
我們也可以嘗試直接用已知不等式:對於正實數 a,b,c 滿足 ab+bc+ca=3,有 a^2+b^2+c^2 ≥ ab+bc+ca =3,並且已知 Schur 不等式: a^3+b^3+c^3+3abc ≥ (a+b+c)(ab+bc+ca)。但這裏 a^2+b^2+c^2 與 a^3 不同。我們也許可以化為 (a+b+c)(ab+bc+ca) = (a+b+c)*3。 Schur 不等式告訴我們 a^3+b^3+c^3+3abc ≥ (a+b+c)(ab+bc+ca) = 3(a+b+c)。但我們需要 a^2+b^2+c^2。可以試着利用均值不等式建立 a^2+b^2+c^2 與 a^3+b^3+c^3 的關係?比如 a^3+b^3+c^3 ≥ (a^2+b^2+c^2)(a+b+c)/3? 這是 Chebyshev 排序不等式?實際上,由 Chebyshev 不等式,如果 a ≥ b ≥ c,則 (a^2+b^2+c^2)/3 ≥ ((a+b+c)/3)^2 等等。但也許有直接的方法。
另一種思路:令 p = a+b+c, q = ab+bc+ca = 3, r = abc。那麼我們要證明的是 a^2+b^2+c^2 + 3r ≥ 6。注意到 a^2+b^2+c^2 = p^2 - 2q = p^2 - 6。所以原不等式變為 (p^2 - 6) + 3r ≥ 6 => p^2 + 3r ≥ 12。所以我們需證明 p^2 + 3r ≥ 12,其中 q = 3,且 a,b,c > 0。
這樣,問題轉化為:對於正實數 a,b,c,滿足 ab+bc+ca = 3,證明 (a+b+c)^2 + 3abc ≥ 12。等價於 (a+b+c)^2 + 3abc ≥ 4(ab+bc+ca)(因為 4*3=12)。實際上這正是已知不等式:對於非負實數 a,b,c,有 (a+b+c)^2 + 9abc/(a+b+c) ≥ 4(ab+bc+ca) 嗎?不是。
考慮 Schur 不等式:對於任意非負實數 a,b,c,有 a^3+b^3+c^3+3abc ≥ (a+b+c)(ab+bc+ca)。但我們可以用 Schur 不等式推出關於 p,q,r 的關係: Schur 不等式等價於 p^3 + 9r ≥ 4pq(實際上標準形式:a^3+b^3+c^3+3abc ≥ a^2(b+c)+b^2(c+a)+c^2(a+b) 可化為 p^3 - 4pq + 9r ≥ 0)。讓我們推導一下:
已知恆等式:a^3+b^3+c^3 = p^3 - 3pq + 3r。(因為 (a+b+c)^3 = a^3+b^3+c^3 + 3(a+b)(b+c)(c+a),但標準恆等式:a^3+b^3+c^3 - 3abc = (a+b+c)(a^2+b^2+c^2 - ab - bc - ca) = p(p^2 - 3q) = p^3 - 3pq。所以 a^3+b^3+c^3 = p^3 - 3pq + 3r?Wait 檢查:
由 (a+b+c)^3 = a^3+b^3+c^3 + 3(a+b)(b+c)(c+a)。而 (a+b)(b+c)(c+a) = (p - c)(p - a)(p - b)? 更好用標準恆等式:a^3 + b^3 + c^3 - 3abc = (a+b+c)(a^2+b^2+c^2 - ab - bc - ca)。而 a^2+b^2+c^2 - ab - bc - ca = (1/2)[(a-b)^2+(b-c)^2+(c-a)^2]。所以
a^3+b^3+c^3 - 3r = p (p^2 - 2q - q?) 注意:a^2+b^2+c^2 = p^2 - 2q。所以 a^2+b^2+c^2 - (ab+bc+ca) = p^2 - 3q。因此:
a^3+b^3+c^3 - 3r = p(p^2 - 3q) = p^3 - 3pq。
於是 a^3+b^3+c^3 = p^3 - 3pq + 3r。
現在 Schur 不等式: a^3+b^3+c^3 + 3r ≥ a^2(b+c) + b^2(c+a) + c^2(a+b)。右邊 = Σ a^2(b+c) = (a^2b + a^2c) + ... = (ab+bc+ca)(a+b+c) - 3abc = pq - 3r。因為 Σ a^2(b+c) = (a+b+c)(ab+bc+ca) - 3abc = pq - 3r。
因此 Schur 不等式變為:
(p^3 - 3pq + 3r) + 3r ≥ pq - 3r => p^3 - 3pq + 6r ≥ pq - 3r => p^3 - 3pq - pq + 6r + 3r ≥ 0? 我們移項:
p^3 - 3pq + 6r - (pq - 3r) ≥ 0 => p^3 - 3pq + 6r - pq + 3r ≥ 0 => p^3 - 4pq + 9r ≥ 0。
所以 Schur 不等式等價於 p^3 - 4pq + 9r ≥ 0。
現在我們有 q = 3。所以 Schur 給出 p^3 - 12p + 9r ≥ 0 => p^3 + 9r ≥ 12p。
但我們想要的是 p^2 + 3r ≥ 12。不知道能不能從 Schur 推出。考慮利用 AM-GM 或其他不等式建立 p 和 r 的關係。因為 q 固定,p 有最小值。由已知 q=3,根據 (a+b+c)^2 ≥ 3(ab+bc+ca) = 9,所以 p ≥ 3。當 a=b=c=1 時取等。 p 的上界?可以任意大,比如 a 很大,b,c 很小滿足 ab+ac+bc=3,但 p 可能也很大?例如 a→∞,則 b,c→0 但乘積和有限,p 可以很大。所以 p 是無上界的。但我們要證 p^2+3r ≥12。當 p 很大時,左邊 p^2 也很大,顯然大於12。所以難點可能在 p 接近最小值 3 時,此時 r 相對較小。我們需要證明在 p 接近 3 時不等式仍成立。由於 p^2+3r 在 a=b=c=1 時等於9+3=12。如果 p 增大,p^2 變大,但 r 可能變小?然而 r 也可能隨 p 增大而可能變化。但整體 p^2 增長很快,所以應當成立。所以關鍵在於證明 p^2+3r 在約束下在 a=b=c=1 處取最小值 12。這可以是一個優化問題:在 ab+bc+ca=3 且 a,b,c>0 條件下,求 f = p^2+3r 的最小值。我們要證明最小值為12。由於對稱性,極值可能出現在相等點或邊界(比如某些變量趨於0?但 a,b,c>0,但可以趨近於0,然而 ab+bc+ca=3,如果某個變量趨於0,其他兩個乘積必須有限,比如 a→0,則 bc≈3,那麼 b,c 至少 sqrt(3) >1,p = a+b+c 大約 b+c,而 r = abc →0,所以 f ≈ (b+c)^2 + 0 = b^2+c^2+2bc。又 bc=3,且由 b^2+c^2 ≥ 2bc =6,所以 f ≥ 6+6=12? 實際上 b^2+c^2+2bc = (b+c)^2,但 b^2+c^2 = (b+c)^2 - 2bc。所以 f ≈ (b+c)^2,而 (b+c)^2 = b^2+c^2+2bc ≥ 2bc+2bc=4bc=12,當 b=c 時等號成立。所以 f ≈ (b+c)^2 ≥ 12,當 b=c 時等號可達? 但 a→0,b=c=√3,則 f ≈ (2√3)^2 = 12,r=0,所以 f →12+? 但嚴格正 a>0,可能稍大於12。所以邊界最小值似乎也是12。因此我們猜測最小值是12,在 a=b=c=1 處取得,也可能在邊界 a→0, b=c=√3 時取到12但 a=0 不在正實數內(極限)。所以對於正實數,最小值可能 >12? 實際上,當 a 趨近於0時,b 和 c 趨近於 √3,則 p^2+3r 趨近於12,但 r = a*b*c 趨近於0,p^2 趨近於 (b+c)^2 = (2√3)^2 =12。所以極限值為12,但不可達。同樣地,若 a,b,c 都 >0,最小值可能恰好12在 a=b=c=1 達到。所以不等式成立,且當 a=b=c=1 時取等。所以需要證明 p^2+3r ≥12。
證明方法1:使用 uvw 方法。令 a,b,c 是正實數,q = 3 固定。我們要證 p^2+3r ≥12。由 Schur 不等式,我們有 p^3+9r ≥12p => r ≥ (12p - p^3)/9。代入 f = p^2 + 3r ≥ p^2 + 3*(12p - p^3)/9 = p^2 + (12p - p^3)/3 = p^2 + 4p - p^3/3。所以我們需要證明 p^2 + 4p - p^3/3 ≥ 12,即乘以3:3p^2 + 12p - p^3 ≥ 36 => -p^3 + 3p^2 + 12p - 36 ≥ 0 => 移項: p^3 - 3p^2 - 12p + 36 ≤ 0? 不對,我們整理:
f_min 的估計: f ≥ g(p) = p^2 + 4p - p^3/3。
需要證明 g(p) ≥ 12 對於所有可能的 p(即滿足存在 a,b,c>0, ab+bc+ca=3 的 p 的範圍)。p 的取值範圍是什麼?由 q=3,根據已知不等式:對於正實數 a,b,c,有 (a+b+c)^2 ≥ 3(ab+bc+ca) = 9,所以 p ≥ 3。另外,p 的上界無限制,但 g(p) 在 p 增大時會怎樣? g(p) = -p^3
----------------------------------------
模型最終答案:
============================================================
測試問題 2 [算法與編程邏輯]:
問題: 設計一個算法,判定一個有向圖是否為單連通的(即任意兩點之間至多隻有一條簡單路徑)。請描述思路、給出時間複雜度分析,並用Python實現關鍵部分。
----------------------------------------
模型思考過程:
我們被要求設計一個算法判定一個有向圖是否為單連通的。單連通的定義:對於任意兩個頂點u和v,至多隻有一條簡單路徑(即沒有重複頂點的路徑)從u到v。注意是“至多隻有一條”,可以沒有路徑,也可以有一條,但不能有兩條或更多條不同的簡單路徑。
這類似於有向圖中任意兩點之間不存在兩條不同的簡單路徑。這讓我聯想到有向圖的“單連通性”的概念在圖論中。通常,有向圖的單連通性判定是NP-hard的嗎?我記得對於有向圖,判定“是否存在一對頂點之間有兩條點不相交(除了端點)的路徑”是多項式時間可解的,例如使用最大流可以檢驗點或邊的雙連通性。但這裏的條件更強:任意兩點之間至多隻有一條簡單路徑。也就是説,圖中不能存在兩個不同的頂點序列形成兩條簡單路徑從u到v。
讓我們思考:什麼圖滿足這個性質?一個DAG(有向無環圖)是否一定滿足?不一定,DAG中也可能有兩條簡單路徑從u到v,例如 u->a->v 和 u->b->v。所以不是所有DAG都滿足。實際上,有向樹(有向的樹,例如每個節點只有一個入度或出度?)可能是滿足的,但也不一定。確切地説,這種圖是被稱為“有向樹”或者“有向森林”嗎?但森林中從根到葉子有唯一路徑,但任意兩點之間至多有一條路徑嗎?在無向樹中,任意兩點之間恰好有一條簡單路徑。對於有向樹,如果是有根樹並且所有邊都從父指向子,那麼從祖先到後代有唯一路徑,但反過來(從後代到祖先)沒有路徑,所以滿足至多一條。但是,如果有交叉或者共享結構,可能會產生多條路徑?例如下圖:節點 A 指向 B 和 C,B 和 C 都指向 D。那麼從 A 到 D 有兩條路徑 A->B->D 和 A->C->D。所以不是單連通。因此這個圖包含一個“匯合”點,使得從某個點出發通過不同分支到達同一點。這類似圖中存在一個點對之間有兩條路徑。這實際上是圖中存在一個點 v 有兩個不同的前驅(或更一般地説,存在點對 u,v 使得存在兩條不同的 u-v 路徑)。
這讓我想起有向圖中“單連通”的判定問題是 NP-hard 嗎?我有點不確定。我查閲回憶:在《算法導論》或圖論中,有向圖的單連通性判定是 co-NP-complete? 實際上,我記得判定一個有向圖是否為“單連通”是多項式時間的?讓我們思考。
問題:給定有向圖 G=(V,E),問是否對於所有頂點對 (u,v),最多有一條簡單路徑。等價於:不存在 u,v 使得存在兩條不同的簡單路徑從 u 到 v。
我們可以這樣考慮:如果有兩條不同的簡單路徑從 u 到 v,那麼這兩條路徑必然在某個點分叉然後又匯合。這構成了一個“有向環”結構?實際上,兩條路徑形成一個“有向環”(不一定簡單?)。因為從 u 出發,一條路徑 P1,另一條 P2,它們都到 v。考慮從 u 開始沿着 P1 到 v,然後從 v 反向沿着 P2(如果邊是反向的,但圖是有向的,不能反向)不過我們可以考慮:如果有向圖中存在兩個不同的 u->v 簡單路徑,那麼這兩個路徑組成的並集將包含一個迴路(即循環),但可能不是有向迴路,因為兩條路徑方向一致。實際上,從 u 到 v 的兩條不同路徑,如果取第一條然後從第二條逆着走回去(從 v 到 u),但不允許逆向邊,所以不一定形成有向迴路。但是,它們會形成一個結構,其中有一個頂點在兩條路徑上被訪問兩次?由於是簡單路徑,頂點不重複,所以除了 u 和 v 之外,兩條路徑上的頂點都不相交。這樣的結構就是一個有向“並行”分支,然後合併。這就像一個 diamond 結構:u->a, u->b, a->v, b->v。這就是典型的導致兩條簡單路徑。更復雜的可能是 u->a->c->v 和 u->b->c->v,這時兩條路徑共享一個內部點 c?注意如果共享一個內部點 c,那麼這兩條路徑就不是簡單的?因為簡單路徑要求頂點不重複,但兩條路徑本身各自簡單,但它們共享了頂點 c(除了 u 和 v)。如果兩條路徑共享了中間點,那麼從 u 到 v 的簡單路徑也許只有一條?實際上,如果兩條路徑共享一些中間點,它們就不是完全不同的簡單路徑,因為可能存在多個簡單路徑通過同一個中間點但路徑序列不同。例如 u->a->c->v 和 u->b->c->v,這兩條路徑是不同的簡單路徑(頂點序列分別是 u,a,c,v 和 u,b,c,v),它們共享 c 和 v?c 是內部點,v 是終點,它們都包含 c 和 v。因為簡單路徑允許公共端點嗎?從定義上講,“簡單路徑”是指頂點不重複的路徑。兩條不同的簡單路徑可以從 u 到 v,它們可能共享一些中間頂點(只要各自沒有重複頂點)。所以共享中間頂點是允許的。例如上述例子中,兩條路徑共享 c,但它們仍是從 u 到 v 的兩條不同簡單路徑。所以條件要求不能有兩條不同的簡單路徑。
那麼如何檢測是否存在一對頂點之間存在兩條簡單路徑?可以枚舉所有點對並檢查是否存在兩條點不相交的路徑(除了端點)?點不相交路徑是指內部頂點不相交。但兩條簡單路徑可能共享內部頂點,所以點不相交是更嚴格的情況。然而,如果存在兩條簡單路徑(可能共享內部頂點),那麼就存在一對頂點之間有兩種方式到達。我們可以通過考慮傳遞閉包?如果圖是單連通的,那麼任意兩點之間的可達關係是否構成一個偏序?即如果存在路徑從 u 到 v 和從 v 到 w,那麼從 u 到 w 的路徑是否唯一?也許單連通性等價於該有向圖是“有向無環圖”且其傳遞閉包矩陣是 0-1 矩陣,且滿足某種性質:不存在兩個不同的路徑導致傳遞閉包中出現“可達性”冗餘?但僅僅 DAG 不能保證唯一路徑,如上例。
實際上,單連通有向圖必須是 DAG 嗎?考慮一個有向環:從 a 到 b 再到 c 再到 a。那麼從 a 到 b 有一條路徑 a->b,還有另一條路徑 a->c->? 比如 a->c? 如果環是 a->b, b->c, c->a,那麼從 a 到 b 有一條直接邊 a->b,也有一條 a->c->a->b? 但 a 重複了,不是簡單路徑。簡單路徑不能重複頂點。從 a 到 b 在一個有向環上可能有兩條簡單路徑嗎?假設環長為 3:a->b, b->c, c->a。從 a 到 b:a->b 直接;也可以 a->c->a->b? 但 a 重複,不行;a->c->a? 不行,因為 a 重複。嘗試 a->b->c->a? 那是到 a 的。所以環中每個點到另一個點可能只有一條簡單路徑?例如在有向環上,從一個點到另一個點恰好只有一條簡單路徑(因為環是單一的圈,如果你走圈方向,只有一條,如果反方向不能因為方向限制)。但是有向環可能導致存在兩條簡單路徑嗎?考慮一個更復雜的帶額外邊的環。但單獨一個簡單有向環(每個頂點出度為1)是單連通的?讓我們檢查:有向環 1->2,2->3,3->1。從 1 到 3:路徑 1->2->3 是唯一的;從 1 到 1:有零長度路徑?通常簡單路徑長度 >=0?通常路徑可以是零長度(即從頂點到自身),但這樣的路徑通常不被認為是簡單路徑?我們需要定義:從頂點到自身是否有路徑?通常單連通定義中考慮兩點之間至多隻有一條簡單路徑,對於 u = v 的情況,通常考慮零長度路徑(空路徑)?或者忽略?一般來説,我們通常考慮不同的頂點,或者包括自身的情況。但為了簡化,我們通常只考慮 u != v。自身路徑問題可能 trivial。從 u 到 u 存在迴路路徑,但簡單路徑要求頂點不重複,所以從 u 到 u 的簡單路徑只能是零長度(即 u 本身),因為如果包含邊,就會重複 u。所以從 u 到 u 只有零長度路徑。所以不影響。因此一個有向環可能滿足單連通?但是有向環中有多個頂點,我們檢查是否存在一對頂點之間有兩條不同簡單路徑。在環中,從 1 到 3,只有 1->2->3。不能走 1->2->3->1->2->3 因為重複頂點。所以看起來環是單連通的。但直覺上,環不是樹狀結構,但單連通似乎允許環?考慮更復雜的環:如果環上有弦(額外邊),可能產生兩條路徑。
我們來測試一下:V={1,2,3,4},邊:1->2,2->3,3->4,4->1, 另外 1->3。從 1 到 3:有 1->2->3 和 1->3 兩條簡單路徑。所以不是單連通。所以單連通圖不一定非要是 DAG;可以有環,但只要環上沒有任何其他結構使得兩點間有多條路徑即可。
那麼如何判定單連通性呢?一種樸素方法是枚舉所有點對 (u,v),然後計算從 u 到 v 的簡單路徑數量,但數量可能指數級。我們需要高效算法。
思考:單連通性等價於圖中不存在一對頂點 (u,v) 使得存在兩條不同的有向路徑(可能共享內部頂點)。這類似於檢查有向圖是否是“有向森林”(即每個點入度不超過1?)但環上入度可以是1,出度1,但上面有環的例子是單連通的,但環中每個點入度=1,出度=1,但這是有向偽樹(functional graph)。實際上,如果一個有向圖每個頂點的出度 <= 1,那麼從任何起點出發最多隻有一條路徑(沿着出邊),但可能形成環。這樣任意兩點之間最多有一條路徑嗎?考慮出度 <= 1 的圖,從 u 出發的路徑是唯一的(如果出度為0則路徑終止)。但是從 u 到 v 可能有兩條路徑嗎?由於每個頂點出度最多為1,從 u 出發只能走一條路,所以不可能從 u 出發有兩條不同路徑到達 v。但可能從不同起點到達同一 v?例如 u1 和 u2 分別有路徑到 v,那沒問題。但問題是對固定的 (u,v),要求最多一條路徑。如果每個頂點出度 <=1,那麼對於給定的 u,最多隻有一條從 u 出發的路徑到達任何 v(如果可達的話),因為路徑是確定性向前。所以這樣的圖是單連通的。同樣,如果每個頂點入度 <=1,那麼對於給定的 v,最多隻有一條路徑從任何 u 到 v?但 (u,v) 配對考慮的是從 u 出發的路徑,入度限制不足以保證從 u 出發的唯一性。例如一個節點 v 有多個入邊,但 u 可能通過不同路徑到達 v?考慮 u->a->v 和 u->b->v,且 a 和 b 都指向 v。那麼從 u 出發有兩條不同路徑到 v,而 v 的入度為2,但 u 的出度可能為2。因此出度限制似乎是充分條件:若每個頂點的出度 <= 1,則圖是單連通的。但這不是必要條件,因為存在出度大於1但仍可能是單連通的圖?考慮這樣一個圖:頂點 A 出邊到 B 和 C,但 B 和 C 分別到達不同的匯,沒有公共可達點。比如 A->B, A->C, B->D, C->E。則從 A 到 D 只有一條,到 E 只有一條,到其他點也只有一條。但從 A 到某個既可由 B 到達又可由 C 到達的頂點?假設 D 和 E 是不同的,沒有匯合,那麼從 A 出發沒有兩個路徑到達同一個頂點。所以這個圖可能是單連通的,儘管 A 的出度為2。但如果存在某個頂點 v 同時可以從 B 和 C 到達,那麼就會有多條路徑。所以出度大於1不一定破壞單連通性,只要從不同分支出發不會匯合到同一個頂點。也就是説,圖必須是一個“有向森林”的變體:如果把它看作一個由出邊構建的樹,那麼要求從任何節點出發的不同分支的可達集合不相交(除了源點本身)。這類似於要求圖是“有向無環圖”且任意兩個從同一點出發的不同路徑不會到達同一個點。這有點像要求圖是“有向樹”的集合,但允許合併?合併就會導致多條路徑。實際上,在單連通圖中,對於任意兩個頂點 u 和 v,最多有一條 u->v 路徑。這等價於説圖是“有向無環圖”?不一定,因為有向環可以存在,如上所述。但如果有向環存在,則環上的任意兩個頂點之間也有唯一路徑嗎?在簡單環上,確實唯一。但環可能帶來問題:考慮環上某點有多條出邊?但環本身每個點出度=1。但如果環上某點有額外的出邊到環外,可能會導致多條路徑?例如環 1->2->3->1,額外邊 1->4,2->4。從 1 到 4:有 1->4 和 1->2->4 兩條路徑。所以破壞了單連通。所以環本身沒問題,但如果有額外分支導致匯合就可能出問題。
從另一種觀點:單連通性等價於圖的“路合併”性質:對於任意三個頂點 x,y,z,如果存在路徑從 x 到 z 和從 y 到 z,那麼這些路徑一定是相同的?不完全是。
讓我們考慮圖論中已知結論:對於有向圖,判定“是否對於所有點對最多有一條簡單路徑”是 co-NP-complete 嗎?我覺得可能是多項式時間可解的。我記起一個概念:有向圖的單連通性(singly connected)在《算法導論》中有習題(第22章?)要求給出算法判斷有向圖是否是單連通。我好像記得:對於有向圖,可以通過對每個頂點進行 DFS,並檢查是否有後向邊或交叉邊?類似無向圖中判斷是否有兩條路徑是使用深度優先搜索找回路?但無向圖中,如果存在兩條不同的簡單路徑,則圖包含環。但在有向圖中,即使存在環,也可能仍然是單連通的,如前所述。所以不能簡單地用環檢測。
也許我們可以這樣:單連通等價於不存在頂點 u 和 v 使得有兩條不同的 u->v 路徑。這可以轉化為:對於每一對 (u,v),考慮從 u 開始的 DFS 或 BFS,檢查是否 v 被訪問多次?但 DFS 通常每個節點只訪問一次,無法直接檢測多條路徑。我們可以使用流量:檢查從 u 到 v 是否存在兩條內部頂點不相交的路徑(點不交)是多項式時間(最大流最小割)。但兩條路徑可能共享內部點,共享內部點的情況可以通過收縮某些點轉化為點不交?如果存在兩條簡單路徑(可能共享內部點),那麼肯定存在一對頂點 w 和 z(在路徑上)使得從 w 到 z 有兩條內部頂點不相交的路徑(除了 w 和 z)?例如,考慮兩條路徑 P1 和 P2 從 u 到 v。如果它們共享一些內部點,我們可以考慮第一個分叉點和最後一個匯合點。定義:沿着 P1 和 P2 從 u 出發,找到第一個點 x 使得 P1 和 P2 的下一個頂點不同(即分叉點),然後從 v 往回走找到最後一個匯合點 y。那麼從 x 到 y,這兩條路徑除了 x 和 y 外內部點不相交(因為分叉後直到匯合前不會相交)。所以存在一對頂點 (x,y) 使得有兩條內部點不相交的路徑(除了端點)。所以單連通性等價於圖中不存在任何一對頂點 (x,y) 使得有兩條內部點不相交的 x->y 路徑。注意 x 和 y 可能是相同的嗎?如果兩條路徑在起點 u 就分叉(即 u 有兩條出邊直接到不同點),那麼 x=u,y=v 可能。例如 u->a->v 和 u->b->v,分叉點 x=u,匯合點 y=v,內部點 a,b 不相交。所以檢查是否存在點對 (x,y)(x!=y)使得有兩條內部頂點不相交的路徑。因此問題轉化為:是否存在兩個頂點 s 和 t,使得從 s 到 t 存在兩條頂點不相交(除 s,t)的有向路徑。這就是有向圖的點連通性至少為2的情況。點對 s,t 的局部點連通性 >=2。我們可以對每個點對檢查是否有點不交的路徑 >=2。然而點對數量 O(n^2),每個用最大流(將每個點拆成入點和出點,邊容量為1)可以在 O(min(n^{2/3}, m^{1/2}) * m) 等時間內計算,但總時間可能太高(n^3)。需要更高效的方法。
也許我們可以利用一些性質:單連通性等價於圖中不包含某個禁止子圖(稱為“鑽石”或“M”結構)?更一般地,是否存在兩個頂點之間有兩條路徑,這意味着圖中存在一個“有向環”結構,其中包含至少兩個不同的 s-t 路徑。但我認為我們可以使用以下算法:對每個頂點執行深度優先搜索(DFS),在 DFS 過程中,如果從某個頂點 u 開始,遇到一個已經訪問過的頂點 v,並且存在另一條路徑從 u 到 v,那麼就會發現多條路徑。但標準的 DFS 在遍歷有向圖時,邊分為樹邊、前向邊、後向邊、交叉
----------------------------------------
模型最終答案:
============================================================
測試問題 3 [複雜邏輯推理]:
問題: 三個邏輯學家走進酒吧,酒保問:'你們三個都要啤酒嗎?' 第一個人説:'我不知道。' 第二個人説:'我也不知道。' 第三個人説:'是的,我們都要啤酒。' 請問最初每個人是否想要啤酒?請還原完整的推理過程。
----------------------------------------
模型思考過程:
我們被問到:"三個邏輯學家走進酒吧,酒保問:'你們三個都要啤酒嗎?' 第一個人説:'我不知道。' 第二個人説:'我也不知道。' 第三個人説:'是的,我們都要啤酒。' 請問最初每個人是否想要啤酒?請還原完整的推理過程。"
這是一個經典的邏輯謎題。我們需要分析三個邏輯學家的回答,並推斷他們各自是否想要啤酒。假設他們都是完美邏輯學家,誠實且使用邏輯推理。問題:酒保問:"你們三個都要啤酒嗎?" 這是一個是否問題,詢問是否三個人都想要啤酒。三個人依次回答。第一個人説:"我不知道。" 這意味着從他自己的知識和推理出發,他無法確定是否三個人都要啤酒。第二個人説:"我也不知道。" 第三個人説:"是的,我們都要啤酒。"
我們需要推斷出每個人是否想要啤酒。經典的解答是:第一個人不想要啤酒,第二個人想要啤酒,第三個人想要啤酒。但我們需要驗證並還原推理。
讓我們設定變量:A、B、C分別表示第一個人、第二個人、第三個人的意願(想要啤酒為True,不想要為False)。酒保問的是:是否(A ∧ B ∧ C)?每個人都能聽到其他人的回答,並且每個人都知道自己的意願,但不知道別人的意願。他們都是邏輯學家,會從回答中推斷信息。
我們考慮每個人的推理:
首先,第一個人回答“我不知道”。這意味着從他自己的視角,他無法確定是否三個人都想要啤酒。也就是説,對於他而言,如果他自己不想要啤酒,那麼顯然三個人不可能都想要啤酒(因為他自己不想),那麼他會知道答案為“否”,即不是三個人都要啤酒。所以,如果他可以確定答案為否,他就不會説“我不知道”。相反,如果他自己想要啤酒,那麼答案取決於B和C是否也都想要。由於他不知道B和C的意願,他無法確定是否三個人都要,所以他會説“我不知道”。然而,注意:如果他自己不想要,他應該知道答案為否,所以他會回答“不是”(或類似),而不會説“我不知道”。所以,第一個人説“我不知道”意味着他自己想要啤酒?但我們需要謹慎:他説“我不知道”表示他不確定整體命題的真假。如果他自己想要啤酒,整體命題的真假依賴於B和C。他不知道B和C,所以確實不知道整體是真是假。所以“我不知道”表明他想要啤酒。但是,這是經典謎題的典型答案嗎?實際上經典謎題中,第一個人説“我不知道”表明他想要啤酒。但讓我們繼續。
然而,如果我們認為第一個人想要啤酒,那麼從經典答案看,第一個人不想要?等等,我們來回憶經典版本:有三個人走進酒吧,酒保問“你們都要啤酒嗎?”,第一個人説“我不知道”,第二個人説“我不知道”,第三個人説“是的”。常見推理:第一個人説不知道,説明他不是不想要啤酒,因為如果他不想要,他會直接説“不”,因為那樣就知道不是三個人都要。所以第一個人想要。第二個人聽到第一個人的回答,知道第一個人想要。但是第二個人説不知道,説明他不知道第三個人是否想要,同時他知道自己(第二個人)想要?類似推理:如果第二個人自己不想要,那麼整體一定為假,因為他自己不想要,所以他會回答“不”。所以他説不知道意味着他想要。第三個人聽到前兩個都説不知道,就知道前兩個都想要。那麼如果第三個人自己不想要,他就會回答“不”。但他回答“是的”,説明第三個人也想要。所以所有人都想要。但經典謎題中第三個人説“是的”,就是“是的,我們都要啤酒”,意味着整體為真,且他確認。但問題問“最初每個人是否想要啤酒?”如果第三個人回答“是的,我們都要啤酒”,那説明三個人都想要。然而題目中第三個人説:“是的,我們都要啤酒。”這似乎直接表明了三個都要。那麼推理的結果也是三個人都要。但這就太簡單了?為什麼還需要前兩個人的回答?因為第三個人是陳述了結論,我們需要驗證這是否符合邏輯。第三個人作為邏輯學家,他只會在他知道三個人都要的情況下説“是的”。所以他的回答暗示他知道三個人都要。那麼從他知道的信息,結合前兩人的回答以及自己的意願,他可以推斷出所有人都要。所以這也是一致性條件。
但經典謎題通常有個轉折:第一個人和第二個人都説不知道,第三個人説“是的”,結果得出第一個人不想要,第二個人想要,第三個人想要?不,我記憶中有一個謎題:三個人走進酒吧,酒保問“你們都要啤酒嗎?”,第一個説“我不知道”,第二個説“我不知道”,第三個説“不是”。然後推理得出各自意願。或者另一個版本:三個人走進餐廳,服務員問“你們都要咖啡嗎?”,第一個説“我不知道”,第二個説“我不知道”,第三個説“是的”,結果推理得出三個人都要咖啡。我認為大多數標準答案是三個人都要。讓我查一下記憶:確實有經典的“三個邏輯學家走進酒吧”謎題,結局是三個人都要啤酒。但是網上還有變體:第一個人説“我不知道”,第二個人説“我不知道”,第三個人説“不是”。然後推理出第一個人想要,第二個人想要,第三個人不想要。所以這裏第三個人説“是的”,應該就是三個人都想要。
但是題目問:“請問最初每個人是否想要啤酒?”我們需要給出每個人是否想要。如果是三個人都要,那就是第一個人想要,第二個人想要,第三個人想要。但是我們需要還原完整的推理過程。
但是讓我們再仔細分析一下,因為有些版本的謎題中,第一個人説“我不知道”可以推出他想要,但第二個人説“我不知道”可能推出他不想要?不,如果第二個人不想要,他知道第一個人想要(因為第一個人説不知道意味着他想要),那麼整體(三人都要)為假,他可以直接回答“不是”。所以他説不知道意味着他想要。所以兩個不知道意味着前兩個都想要。然後第三個人聽到兩個不知道,就知道前兩個都想要。如果他想要,那麼整體為真,他會回答“是”;如果他不想要,他會回答“不是”。所以第三個人説“是”表明他想要。所以三個人都想要。
但這樣推理就很簡單,而且第三個人的回答直接就是肯定,所以無需進一步推理就知道三個都要。那麼問題結束。但是題目可能希望我們細緻地推理每個人為什麼那樣回答,得出每個人意願。
然而,我覺得這個謎題可能有些微妙:因為第一個人説“我不知道”,第二個人也説“我不知道”,但第三個人説“是的,我們都要啤酒。” 第三個人是在前兩人都説不知道後説的,他作為邏輯學家,必須基於已知信息做出準確回答。他回答“是的”,表明他知道三個人都要。這必然意味着他自己想要(否則不會説“是的”,因為如果他不想要,他就知道不是三個人都要,就會説“不是”)。並且他還知道前兩人都想要,因為如果前兩人中有人不想要,那麼第三個人即使想要也無法確定整體是否為真?不,第三個人知道自己的意願,也知道前兩人的回答所傳遞的信息。前兩人都説不知道,這傳遞給第三個人的信息是:第一個人想要,第二個人也想要。因此第三個人可以推斷出三個人都要(如果他想要),或不是(如果他不想要)。所以他的回答直接揭示了他的意願。
所以推理結果是:A=真(想要),B=真,C=真。
但是,有沒有其他可能性?讓我們形式化分析。
設命題P = (A ∧ B ∧ C)。酒保問:你們三個都要啤酒嗎?即問P是否為真。
每個人都可以基於自己的意願和聽到的回答來推斷P的真假。他們回答規則:如果他們知道P為真,他們回答“是”;如果他們知道P為假,他們回答“不是”;否則,他們回答“我不知道”。(因為他們都是邏輯學家,所以會誠實且準確。)
我們給定按順序回答:A説“我不知道”,B説“我不知道”,C説“是的”。
我們需要找出可能的(A, B, C)布爾值組合,使得這些回答符合邏輯,並且是公共知識:每個人都知道所有參與者都是邏輯學家,都知道這個回答規則,並且知道每個人都知道...等等。
順序:首先A回答,他只知道自己A的值,不知道B和C。在回答時,他不知道B和C的回答(還沒發生)。所以A基於自己的知識:如果他知道P為假,即他知道(A ∧ B ∧ C)為假,就會説“不是”;如果他知道P為真,就會説“是”;否則説“我不知道”。
什麼時候A知道P為假?因為P = A ∧ B ∧ C,A知道自己的A值。如果A = false,那麼無論B和C如何,P都是false。所以A知道P是false。因此A會回答“不是”。如果A = true,那麼P的真值取決於B和C,A不知道B和C,所以無法確定P是真還是假,所以A不知道P的真假,因此回答“我不知道”。所以A回答“我不知道”當且僅當A = true。如果A = false,他會回答“不是”。因此從A的回答“我不知道”推斷出A = true。
因此我們知道A想要啤酒。
現在B回答。B聽到A的回答,並且知道自己的B值,不知道C的值。B知道A是邏輯學家,因此從A的回答推斷出A = true(如我們剛才推理)。B也知道自己的B。在決定回答時,B考慮是否知道P的真假。
給定A = true(從A的回答得知),P = true ∧ B ∧ C = B ∧ C。所以P的真假取決於B和C。B知道B的值,但不知道C的值。所以:
- 如果B = false,那麼P = false ∧ C = false,無論C是什麼,P都是false。因此B知道P是false。所以B會回答“不是”。
- 如果B = true,那麼P = true ∧ C = C。所以P的真假取決於C,B不知道C,所以B不知道P的真假,因此回答“我不知道”。
B回答“我不知道”,所以必須是B = true。如果B = false,B會回答“不是”。因此從B的回答“我不知道”推斷出B = true。
現在C回答。C聽到A和B的回答。C知道A和B都是邏輯學家,因此從A的回答知道A = true,從B的回答知道B = true。C也知道自己的C值。現在P = A ∧ B ∧ C = true ∧ true ∧ C = C。因此P的真假完全等於C的值。所以C知道P的真假:如果C = true,P = true;如果C = false,P = false。C是邏輯學家,且知道這一點。因此C會根據C的值給出確定回答:如果C = true,他會回答“是”;如果C = false,他會回答“不是”。
給定的實際回答是C説“是的”。因此C = true。
所以結論:A = true,B = true,C = true。三個人都想要啤酒。
這就是完整的推理。這個推理簡單明瞭。
但問題是題目:“三個邏輯學家走進酒吧,酒保問:'你們三個都要啤酒嗎?' 第一個人説:'我不知道。' 第二個人説:'我也不知道。' 第三個人説:'是的,我們都要啤酒。' 請問最初每個人是否想要啤酒?請還原完整的推理過程。”
所以答案就是:三個人都想要啤酒。
現在,我們需要提供完整的推理過程,包括每一步的邏輯。可能還要指出,第一個人説不知道意味着他想要啤酒;第二個人説不知道意味着他想要啤酒;第三個人説意味着他想要啤酒,且由此推出三人都要。
但注意:第三個人説“是的,我們都要啤酒”直接就是肯定整體命題,從推理看也符合他自己想要,而且前兩人也都想要。
因此最終答案:第一個人想要,第二個人想要,第三個人想要。
也許題目有陷阱:也許第一個人説“我不知道”可能是因為他不知道自己是否要?但邏輯學家的意思是他們知道自己是否要啤酒。通常設定是每個人都知道自己的意願,但不知道別人的。所以推理正確。
所以應該回答:三個人都想要啤酒。
但我們也要考慮:有沒有可能某個人説謊或不是完美邏輯?不,給定他們都是邏輯學家,他們誠實且推理正確。
因此最終答案。
但為確保,我們檢查是否有其他可能性。從推理看,如果A回答“我不知道”,則A必為true。否則A會回答“不是”。所以A true是唯一的。同樣B回答“我不知道”且已知A true,則B必為true,否則會回答“不是”。C回答“是”,且已知A true B true,則C必為true,否則會回答“不是”。所以組合唯一:全真。
因此答案清晰。
所以輸出應該包含推理過程。
現在我們需要以合適的方式輸出,作為AI助手,我們要給出答案和推理。
但是,用户要求:“請嚴謹、分步驟地思考並解決問題。” 所以我們需要展示分步驟推理,最後給出結論。
因此,我將按以下步驟:
1. 定義變量,明確規則:每個人誠實,根據自己知道的信息,如果能確定三個人都要啤酒就回答“是”,能確定不是三個人都要就回答“不是”,否則回答“我不知道”。
2. 分析第一個人的回答:
- 如果第一個人自己不想要啤酒,則他知道至少一個人不想要,因此可以確定不是三個人都要,會回答“不是”。
- 如果他想要啤酒,則他無法確定另外兩人的意願,因此無法確定整體是否成立,會回答“我不知道”。
- 他説“我不知道”,因此推出他想要啤酒。
3. 分析第二個人的回答:
- 第二個人聽到了第一個人的回答,由此推斷出第一個人想要啤酒。
- 如果第二個人自己不想要啤酒,則他知道至少一個人(他自己)不想要,因此可以確定不是三個人都要,會回答“不是”。
- 如果他想要啤酒,則整體是否成立取決於第三個人,他不知道第三個人的意願,因此無法確定,會回答“我不知道”。
- 他説“我不知道”,因此推出他想要啤酒。
4. 分析第三個人的回答:
- 第三個人聽到了前兩人的回答,推斷出第一個人和第二個人都想要啤酒。
- 如果第三個人自己不想要啤酒,則他知道不是三個人都要,會回答“不是”。
- 如果他想要啤酒,則他知道三個人都想要,會回答“是”。
- 他説“是的,我們都要啤酒”,因此推出他想要啤酒。
5. 結論:三個人都想要啤酒。
也可以最後總結:最初每個人都想要啤酒。
這就是完整的推理過程。
現在我們輸出。
----------------------------------------
模型最終答案:
根據題意,三個邏輯學家都是完美理性的,他們知道自己是否想要啤酒,但不知道別人的意願。對於酒保的問題“你們三個都要啤酒嗎?”,每個人會根據自己的知識回答:
- 如果能確定三個人都要,回答“是”;
- 如果能確定並非三個人都要,回答“不是”;
- 否則回答“我不知道”。
現在逐步推理。
### 第一步:分析第一個人的回答 “我不知道”
設第一個人、第二個人、第三個人是否想要啤酒分別為 A、B、C(真表示想要)。
第一個人只知道自己的意願 A。
- 如果 A = 假(他不想要),則無論 B、C 如何,A ∧ B ∧ C 為假,他可以確定並非三個人都要,應回答“不是”。
- 如果 A = 真(他想要),則 A ∧ B ∧ C 的真假取決於 B 和 C,而他不知道 B、C,故無法確定,應回答“我不知道”。
實際第一個人説“我不知道”,因此必然 A = 真,即第一個人想要啤酒。
### 第二步:分析第二個人的回答 “我也不知道”
第二個人聽到了第一個人的回答,並根據完美推理得出 A = 真。他自己知道自己的意願 B,但不知道 C。
此時整體命題為 A ∧ B ∧ C = 真 ∧ B ∧ C = B ∧ C。
- 如果 B = 假(他不想要),則 B ∧ C 恆為假,他可以確定並非三個人都要,應回答“不是”。
- 如果 B = 真(他想要),則整體變為 C,而他不知道 C,無法確定,應回答“我不知道”。
實際第二個人説“我也不知道”,因此必然 B = 真,即第二個人想要啤酒。
### 第三步:分析第三個人的回答 “是的,我們都要啤酒”
第三個人聽到了前兩人的回答,根據完美推理得出 A = 真,B = 真。他自己知道自己的意願 C。
此時整體命題為 A ∧ B ∧ C = 真 ∧ 真 ∧ C = C。
- 如果 C = 假(他不想要),則整體為假,他可以確定並非三個人都要,應回答“不是”。
- 如果 C = 真(他想要),則整體為真,他可以確定三個人都要,應回答“是”。
實際第三個人説“是的,我們都要啤酒”,因此必然 C = 真,即第三個人想要啤酒。
### 結論
綜合以上推理:
- 第一個人想要啤酒,
- 第二個人想要啤酒,
- 第三個人想要啤酒。
因此,最初三個人都想要啤酒。
============================================================
✅ 所有測試問題已完成!