題目

We have n jobs, where every job is scheduled to be done from startTime[i] to endTime[i], obtaining a profit of profit[i].

You're given the startTime , endTime and profit arrays, you need to output the maximum profit you can take such that there are no 2 jobs in the subset with overlapping time range.

If you choose a job that ends at time X you will be able to start another job that starts at time X.

Example 1:

1235. Maximum Profit in Job Scheduling_Time

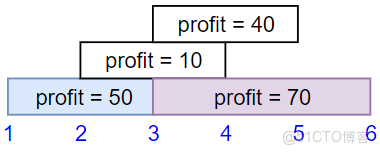
Input: startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
Output: 120
Explanation: The subset chosen is the first and fourth job. 
Time range [1-3]+[3-6] , we get profit of 120 = 50 + 70.

Example 2:

1235. Maximum Profit in Job Scheduling_Time_02

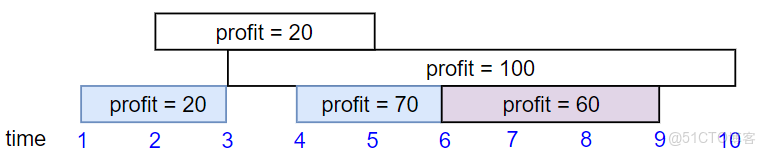
Input: startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
Output: 150
Explanation: The subset chosen is the first, fourth and fifth job. 
Profit obtained 150 = 20 + 70 + 60.

Example 3:

1235. Maximum Profit in Job Scheduling_Time_03

Input: startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
Output: 6

Constraints:

  • 1 <= startTime.length == endTime.length == profit.length <= 5 * 10^4
  • 1 <= startTime[i] < endTime[i] <= 10^9
  • 1 <= profit[i] <= 10^4

題目大意

你打算利用空閒時間來做兼職工作賺些零花錢。這裏有 n 份兼職工作，每份工作預計從 startTime[i] 開始到 endTime[i] 結束，報酬為 profit[i]。給你一份兼職工作表，包含開始時間 startTime，結束時間 endTime 和預計報酬 profit 三個數組，請你計算並返回可以獲得的最大報酬。注意，時間上出現重疊的 2 份工作不能同時進行。如果你選擇的工作在時間 X 結束，那麼你可以立刻進行在時間 X 開始的下一份工作。

提示：

  • 1 <= startTime.length == endTime.length == profit.length <= 5 * 10^4
  • 1 <= startTime[i] < endTime[i] <= 10^9
  • 1 <= profit[i] <= 10^4

解題思路

  • 給出一組任務，任務有開始時間，結束時間，和任務收益。一個任務開始還沒有結束，中間就不能再安排其他任務。問如何安排任務，能使得最後收益最大？
  • 一般任務的題目，區間的題目，都會考慮是否能排序。這一題可以先按照任務的結束時間從小到大排序，如果結束時間相同，則按照收益從小到大排序。dp[i] 代表前 i 份工作能獲得的最大收益。初始值，dp[0] = job[1].profit 。對於任意一個任務 i ，看能否找到滿足 jobs[j].enTime <= jobs[j].startTime && j < i 條件的 j，即查找 upper_bound 。由於 jobs 被我們排序了，所以這裏可以使用二分搜索來查找。如果能找到滿足條件的任務 j，那麼狀態轉移方程是：dp[i] = max(dp[i-1], jobs[i].profit)。如果能找到滿足條件的任務 j，那麼狀態轉移方程是：dp[i] = max(dp[i-1], dp[low]+jobs[i].profit)。最終求得的解在 dp[len(startTime)-1] 中。 中。

參考代碼

package leetcode

import "sort"

type job struct {
	startTime int
	endTime   int
	profit    int
}

func jobScheduling(startTime []int, endTime []int, profit []int) int {
	jobs, dp := []job{}, make([]int, len(startTime))
	for i := 0; i < len(startTime); i++ {
		jobs = append(jobs, job{startTime: startTime[i], endTime: endTime[i], profit: profit[i]})
	}
	sort.Sort(sortJobs(jobs))
	dp[0] = jobs[0].profit
	for i := 1; i < len(jobs); i++ {
		low, high := 0, i-1
		for low < high {
			mid := low + (high-low)>>1
			if jobs[mid+1].endTime <= jobs[i].startTime {
				low = mid + 1
			} else {
				high = mid
			}
		}
		if jobs[low].endTime <= jobs[i].startTime {
			dp[i] = max(dp[i-1], dp[low]+jobs[i].profit)
		} else {
			dp[i] = max(dp[i-1], jobs[i].profit)
		}
	}
	return dp[len(startTime)-1]
}

func max(a int, b int) int {
	if a > b {
		return a
	}
	return b
}

type sortJobs []job

func (s sortJobs) Len() int {
	return len(s)
}
func (s sortJobs) Less(i, j int) bool {
	if s[i].endTime == s[j].endTime {
		return s[i].profit < s[j].profit
	}
	return s[i].endTime < s[j].endTime
}
func (s sortJobs) Swap(i, j int) {
	s[i], s[j] = s[j], s[i]
}