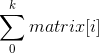題目

Given a matrix, and a target, return the number of non-empty submatrices that sum to target.

A submatrix x1, y1, x2, y2 is the set of all cells matrix[y] with x1 <= x <= x2 and y1 <= y <= y2.

Two submatrices (x1, y1, x2, y2) and (x1', y1', x2', y2') are different if they have some coordinate that is different: for example, if x1 != x1'.

Example 1:

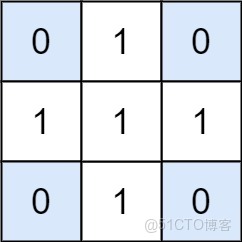
1074. Number of Submatrices That Sum to Target_暴力解法

Input: matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0
Output: 4
Explanation: The four 1x1 submatrices that only contain 0.

Example 2:

Input: matrix = [[1,-1],[-1,1]], target = 0
Output: 5
Explanation: The two 1x2 submatrices, plus the two 2x1 submatrices, plus the 2x2 submatrix.

Note:

  1. 1 <= matrix.length <= 300
  2. 1 <= matrix[0].length <= 300
  3. -1000 <= matrix[i] <= 1000
  4. -10^8 <= target <= 10^8

題目大意

給出矩陣 matrix 和目標值 target，返回元素總和等於目標值的非空子矩陣的數量。

子矩陣 x1, y1, x2, y2 是滿足 x1 <= x <= x2 且 y1 <= y <= y2 的所有單元 matrix[x][y] 的集合。

如果 (x1, y1, x2, y2) 和 (x1', y1', x2', y2') 兩個子矩陣中部分座標不同（如：x1 != x1'），那麼這兩個子矩陣也不同。

提示：

  1. 1 <= matrix.length <= 300
  2. 1 <= matrix[0].length <= 300
  3. -1000 <= matrix[i] <= 1000
  4. -10^8 <= target <= 10^8

解題思路

  • 給出一個矩陣，要求在這個矩陣中找出子矩陣的和等於 target 的矩陣個數。
  • 這一題讀完題感覺是滑動窗口的二維版本。如果把它拍扁，在一維數組中，求連續的子數組和為 target，這樣就很好做。如果這題不降維，純暴力解是 O(n^6)。如何優化降低時間複雜度呢？
  • 聯想到第 1 題 Two Sum 問題，可以把 2 個數求和的問題優化到 O(n)。這裏也用類似的思想，用一個 map 來保存行方向上曾經出現過的累加和，相減就可以得到本行的和。這裏可能讀者會有疑惑，為什麼不能每一行都單獨保存呢？為什麼一定要用累加和相減的方式來獲取每一行的和呢？因為這一題要求子矩陣所有解，如果只單獨保存每一行的和，只能求得小的子矩陣，子矩陣和子矩陣組成的大矩陣的情況會漏掉(當然再循環一遍，把子矩陣累加起來也可以，但是這樣就多了一層循環了)，例如子矩陣是 1*4 的，但是 2 個這樣的子矩陣摞在一起形成 2 * 4 也能滿足條件，如果不用累加和的辦法，只單獨存每一行的和，最終還要有組合的步驟。經過這樣的優化，可以從 O(n^6) 優化到 O(n^4)，能 AC 這道題，但是時間複雜度太高了。如何優化？
  • 首先，子矩陣需要上下左右 4 個邊界，4 個變量控制循環就需要 O(n^4)，行和列的區間累加還需要 O(n^2)。行和列的區間累加可以通過 preSum 來解決。例如 sum[i,j] = sum[j] - sum[i - 1]，其中 sum[k] 中存的是從 0 到 K 的累加和：

    • 1074. Number of Submatrices That Sum to Target_時間複雜度_02

  • 那麼一個區間內的累加和可以由這個區間的右邊界減去區間左邊界左邊的那個累加和得到(由於是閉區間，所需要取左邊界左邊的和)。經過這樣的處理，列方向的維度就被我們拍扁了。
  • 再來看看行方向的和，現在每一列的和都可以通過區間相減的方法得到。那麼這道題就變成了第 1 題 Two Sum 的問題了。Two Sum 問題只需要 O(n) 的時間複雜度求解，這一題由於是二維的，所以兩個列的邊界還需要循環，所以最終優化下來的時間複雜度是 O(n^3)。計算 presum 可以直接用原數組，所以空間複雜度只有一個 O(n) 的字典。
  • 類似思路的題目有第 560 題，第 304 題。 304 題。

參考代碼

package leetcode

func numSubmatrixSumTarget(matrix [][]int, target int) int {
	m, n, res := len(matrix), len(matrix[0]), 0
	for row := range matrix {
		for col := 1; col < len(matrix[row]); col++ {
			matrix[row][col] += matrix[row][col-1]
		}
	}
	for i := 0; i < n; i++ {
		for j := i; j < n; j++ {
			counterMap, sum := make(map[int]int, m), 0
			counterMap[0] = 1 // 題目保證一定有解，所以這裏初始化是 1
			for row := 0; row < m; row++ {
				if i > 0 {
					sum += matrix[row][j] - matrix[row][i-1]
				} else {
					sum += matrix[row][j]
				}
				res += counterMap[sum-target]
				counterMap[sum]++
			}
		}
	}
	return res
}

// 暴力解法 O(n^4)
func numSubmatrixSumTarget1(matrix [][]int, target int) int {
	m, n, res, sum := len(matrix), len(matrix[0]), 0, 0
	for i := 0; i < n; i++ {
		for j := i; j < n; j++ {
			counterMap := map[int]int{}
			counterMap[0] = 1 // 題目保證一定有解，所以這裏初始化是 1
			sum = 0
			for row := 0; row < m; row++ {
				for k := i; k <= j; k++ {
					sum += matrix[row][k]
				}
				res += counterMap[sum-target]
				counterMap[sum]++
			}
		}
	}
	return res
}

// 暴力解法超時！ O(n^6)
func numSubmatrixSumTarget2(matrix [][]int, target int) int {
	res := 0
	for startx := 0; startx < len(matrix); startx++ {
		for starty := 0; starty < len(matrix[startx]); starty++ {
			for endx := startx; endx < len(matrix); endx++ {
				for endy := starty; endy < len(matrix[startx]); endy++ {
					if sumSubmatrix(matrix, startx, starty, endx, endy) == target {
						//fmt.Printf("startx = %v, starty = %v, endx = %v, endy = %v\n", startx, starty, endx, endy)
						res++
					}
				}
			}
		}
	}
	return res
}

func sumSubmatrix(matrix [][]int, startx, starty, endx, endy int) int {
	sum := 0
	for i := startx; i <= endx; i++ {
		for j := starty; j <= endy; j++ {
			sum += matrix[i][j]
		}
	}
	return sum
}