題目

Two players play a turn based game on a binary tree. We are given the root of this binary tree, and the number of nodes n in the tree. n is odd, and each node has a distinct value from 1 to n.

Initially, the first player names a value x with 1 <= x <= n, and the second player names a value y with 1 <= y <= n and y != x. The first player colors the node with value x red, and the second player colors the node with value y blue.

Then, the players take turns starting with the first player. In each turn, that player chooses a node of their color (red if player 1, blue if player 2) and colors an uncolored neighbor of the chosen node (either the left child, right child, or parent of the chosen node.)

If (and only if) a player cannot choose such a node in this way, they must pass their turn. If both players pass their turn, the game ends, and the winner is the player that colored more nodes.

You are the second player. If it is possible to choose such a y to ensure you win the game, return true. If it is not possible, return false.

Example 1:

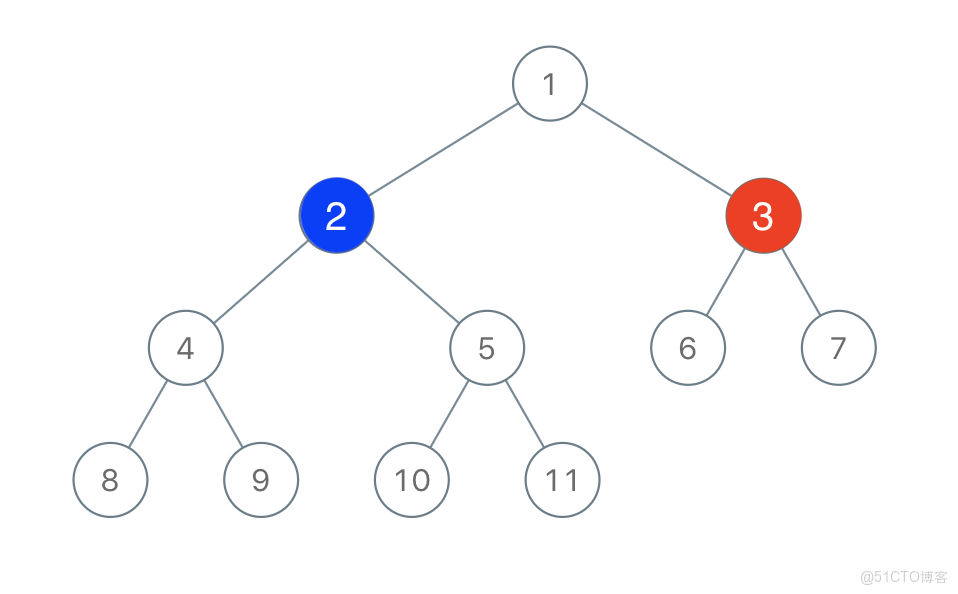
Input: root = [1,2,3,4,5,6,7,8,9,10,11], n = 11, x = 3
Output: true
Explanation: The second player can choose the node with value 2.

Constraints:

• root is the root of a binary tree with n nodes and distinct node values from 1 to n.
• n is odd.
• 1 <= x <= n <= 100

題目大意

有兩位極客玩家參與了一場「二叉樹着色」的遊戲。遊戲中，給出二叉樹的根節點 root，樹上總共有 n 個節點，且 n 為奇數，其中每個節點上的值從 1 到 n 各不相同。遊戲從「一號」玩家開始（「一號」玩家為紅色，「二號」玩家為藍色），最開始時，

• 「一號」玩家從 [1, n] 中取一個值 x（1 <= x <= n）；
• 「二號」玩家也從 [1, n] 中取一個值 y（1 <= y <= n）且 y != x。
• 「一號」玩家給值為 x 的節點染上紅色，而「二號」玩家給值為 y 的節點染上藍色。

之後兩位玩家輪流進行操作，每一回合，玩家選擇一個他之前塗好顏色的節點，將所選節點一個 未着色 的鄰節點（即左右子節點、或父節點）進行染色。如果當前玩家無法找到這樣的節點來染色時，他的回合就會被跳過。若兩個玩家都沒有可以染色的節點時，遊戲結束。着色節點最多的那位玩家獲得勝利 ✌️。現在，假設你是「二號」玩家，根據所給出的輸入，假如存在一個 y 值可以確保你贏得這場遊戲，則返回 true；若無法獲勝，就請返回 false。

提示：

• 二叉樹的根節點為 root，樹上由 n 個節點，節點上的值從 1 到 n 各不相同。
• n 為奇數。
• 1 <= x <= n <= 100

解題思路

• 2 個人參加二叉樹着色遊戲。二叉樹節點數為奇數。1 號玩家和 2 號玩家分別在二叉樹上選項一個點着色。每一回合，玩家選擇一個他之前塗好顏色的節點，將所選節點一個 未着色 的鄰節點（即左右子節點、或父節點）進行染色。當有人不能選點着色的時候，他的那個回合會被跳過。雙方都沒法繼續着色的時候遊戲結束。着色多的人獲勝。問二號玩家是否存在必勝策略？

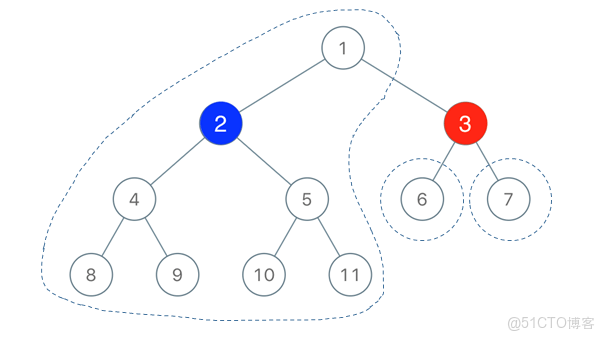
• 如圖所示，當一號玩家選擇了一個紅色的結點，可能會將二叉樹切割為 3 個部分（連通分量），如果選擇的是根結點，則可能是 2 個部分或 1 個部分，如果選擇葉結點，則是 1 個部分。不過無論哪種情況都無關緊要，我們都可以當成 3 個部分來對待，例如一號玩家選擇了一個葉結點，我們也可以把葉結點的左右兩個空指針看成大小為 0 的兩個部分。
• 那麼二號玩家怎樣選擇藍色結點才是最優呢？答案是：選擇離紅色結點最近，且所屬連通分量規模最大的那個點。也就是示例圖中的 1 號結點。如果我們選擇了 1 號結點為藍色結點，那麼可以染成紅色的點就只剩下 6 號點和 7 號點了，而藍色可以把根結點和其左子樹全部佔據。
• 如何確定藍色是否有必勝策略，就可以轉換為，被紅色點切割的三個連通分量中，是否存在一個連通分量，大小大於所有結點數目的一半。統計三個連通分量大小的過程，可以用深度優先搜索（DFS）來實現。當遍歷到某一結點，其結點值等於選定的紅色結點時，我們統計這個結點的左子樹 red_left 和右子樹 red_right 的大小，那麼我們就已經找到兩個連通分量的大小了，最後一個父結點連通分量的大小，可以用結點總數減去這兩個連通分量大小，再減去紅色所佔結點，即 parent = n - red_left - red_right - 1。

參考代碼

func btreeGameWinningMove(root *TreeNode, n int, x int) bool {
	var left, right int
	dfsBtreeGameWinningMove(root, &left, &right, x)
	up := n - left - right - 1
	n /= 2
	return left > n || right > n || up > n
}

func dfsBtreeGameWinningMove(node *TreeNode, left, right *int, x int) int {
	if node == nil {
		return 0
	}
	l, r := dfsBtreeGameWinningMove(node.Left, left, right, x), dfsBtreeGameWinningMove(node.Right, left, right, x)
	if node.Val == x {
		*left, *right = l, r
	}
	return l + r + 1
}