在現代數據科學與人工智能研究中，數據的規模與複雜性呈指數增長。每一個高維數據集不僅包含大量觀測值，還藴含着潛在的結構信息，這些結構可能體現為樣本之間的相似性、變量之間的相關性，或更高階的非線性模式。面對這樣的數據，人類直覺和簡單統計方法往往難以捕捉其內在規律。無監督學習因此成為理解複雜數據的核心工具，其中聚類與降維是最基礎也是最重要的兩類方法。

聚類強調在無標籤條件下發現樣本之間的羣體關係，即哪些樣本更相似、可以被劃分到同一組。它關注的是“樣本層面”的結構，通過度量相似性和差異性，將數據分解為若干簇。降維則從另一個角度出發，關注“特徵層面”的結構。它試圖將高維特徵空間壓縮到低維空間，同時儘可能保留數據的主要信息。這種壓縮不僅降低計算複雜性，也幫助人類理解數據的全局幾何結構。

乍看之下，聚類與降維似乎各自獨立，服務於不同的目標：一個是分類、一個是映射。然而深入分析會發現，它們在數學本質、幾何解釋和信息論框架下具有密切聯繫。降維能夠改善聚類的效果，使得高維數據在低維嵌入中更容易被區分；而聚類的結果也可以驗證降維所揭示的數據結構是否合理。二者共同構成了數據理解的兩種互補策略：從局部相似到全局結構，從離散劃分到連續映射。

1 聚類的理論基礎

聚類（Clustering）是無監督學習中的核心任務，其目標是將數據集劃分為若干簇，使得簇內樣本相似度最大化，簇間樣本差異最大化。設數據集為

聚類的任務是尋找一個簇劃分集合

滿足

並優化某個相似性度量，使簇內距離最小，簇間距離最大。

1.1 距離度量與相似性

聚類的數學核心是定義樣本間的相似性。最常見的度量是歐式距離：

當數據維度較高時，歐式距離容易出現“距離集中現象”，即高維空間中不同樣本間的距離趨於相等，使得聚類判定困難。此時可採用其他度量，如：

• 馬氏距離（Mahalanobis distance）
  
  其中為協方差矩陣，考慮了特徵間的相關性。
• 餘弦相似度（Cosine similarity）
  
  適合文本或高維稀疏向量場景。

1.2 主要聚類算法

1.2.1 劃分式方法

K-Means是最經典的劃分式聚類算法，其優化目標是最小化簇內平方誤差（SSE）：

其中為簇的中心：

K-Means通過迭代實現：

1. 固定簇中心，分配樣本到最近簇；
2. 固定簇分配，更新簇中心； 直到收斂。

1.2.2 層次式方法

層次聚類通過計算樣本距離矩陣，遞歸地進行簇合並（凝聚式）或簇劃分（劃分式）。其結果形成樹狀結構（Dendrogram），可通過截斷不同高度選擇簇數。

1.2.3 密度式方法

密度聚類（如DBSCAN）定義簇為樣本點密度高的區域，核心思想是：

• 若樣本點周圍鄰域內點數 MinPts，則該點為核心點；
• 相鄰核心點構成簇，非核心但密度可達的點加入簇。

密度聚類可以識別任意形狀的簇，並對噪聲樣本進行剔除。

1.3 聚類的優化目標本質

聚類算法的核心目標是最大化簇內相似度、最小化簇間差異。以K-Means為例，優化問題可表示為：

對於譜聚類（Spectral Clustering），通過構建相似度矩陣和圖拉普拉斯矩陣：

再計算的前個特徵向量，映射到低維空間後執行K-Means，實現非線性簇的識別。

2 降維的理論基礎

降維（Dimensionality Reduction）旨在將高維數據映射到低維空間，同時保留原始數據的主要結構信息。設數據矩陣，降維映射為

2.1 線性降維：PCA

主成分分析（PCA）通過尋找方差最大的方向，將高維數據投影到低維子空間。其數學形式為：

1. 構建協方差矩陣：
   
2. 求特徵值分解：
   
   選擇前個最大特徵值對應的特徵向量作為投影矩陣。
3. 得到低維表示：
   

PCA的優化目標是最大化投影數據方差：

2.2 非線性降維

對於高維流形數據，線性方法無法充分捕捉複雜結構。常用非線性降維方法包括：

• ISOMAP：保持樣本間測地距離，最小化低維嵌入與原測地距離的差異。
• LLE（Locally Linear Embedding）：保持局部線性重建關係，優化目標為：其中為局部線性重建權重。
• t-SNE：保持高維空間相鄰概率分佈，優化低維概率分佈與高維分佈的Kullback-Leibler散度：

2.3 降維的數學目標

降維的本質是信息保留最大化與維度壓縮的平衡。可從信息論角度描述：

• 為原始數據，為低維表示；
• 優化目標為最大化互信息：

同時，降維能夠去除冗餘特徵和噪聲，使得後續算法（如聚類或分類）更穩定、高效。

3 聚類與降維的區別

雖然聚類與降維都屬於無監督學習的範疇，但它們在理論目標與數學對象上有明顯區別。

比較維度	聚類	降維
目標	對樣本進行分組	對特徵進行壓縮
輸入	樣本點	特徵矩陣
輸出	類別標籤或簇結構	低維表示
數學核心	相似度最大化	信息保留最大化
優化方向	樣本層面	特徵層面
幾何意義	劃分空間區域	尋找低維子空間

更精確地説，聚類在樣本集合上定義了一個等價關係，若，則它們屬於同一簇。而降維則在特徵空間中定義了一個映射，其約束是與之間的距離儘量反映與在原空間中的距離。

換句話説，聚類是離散化，降維是連續映射。聚類的結果是分類結構；降維的結果是嵌入座標。

4 聚類與降維的聯繫

儘管二者目標不同，但它們在理論上和實踐中有密切聯繫，尤其是在高維數據處理的流程中。

（1）降維為聚類提供結構簡化

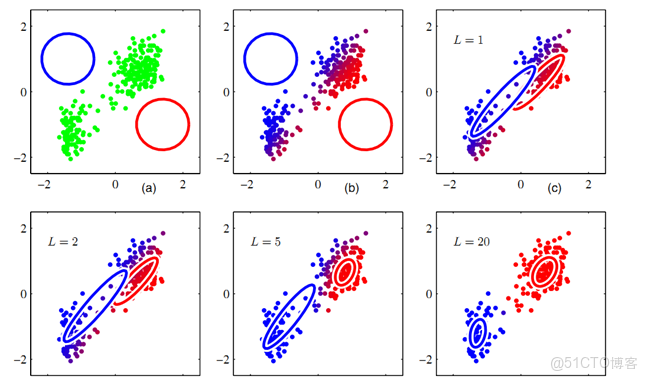
在高維空間中，距離度量容易失效，聚類算法可能難以區分簇之間差異。此時，降維可先將數據映射到低維空間中，保留主要結構特徵。例如，使用PCA或t-SNE可以幫助K-Means更準確地劃分非線性簇。

從數學上看，若是保持局部鄰域的映射，則在低維空間中計算的距離與原空間距離的單調性得以近似保持，從而提升聚類的魯棒性。

（2）聚類反映降維的結果合理性

降維方法的可解釋性常常通過聚類結果驗證。例如，在t-SNE二維可視化中，若樣本自然形成多個緊密區域，説明降維過程成功保留了樣本間的相似性結構。這種視覺聚類驗證了降維映射的有效性。

（3）聯合優化模型

在一些高階算法中，聚類與降維被聯合建模。例如：

• 譜聚類（Spectral Clustering）：通過特徵分解實現隱式降維，再在低維特徵空間上執行K-Means。
• Subspace Clustering（子空間聚類）：認為不同簇可能分佈在不同的低維子空間中，因而聚類過程本身即是降維的分解。
• Deep Embedding Clustering (DEC)：通過神經網絡同時學習低維表示與簇分佈。

這些方法説明，在現代機器學習框架中，聚類與降維已經不再是獨立的兩個階段，而是共同構成無監督表示學習的統一體系。

5 從信息論角度的聯繫

從信息論的視角來看，聚類與降維都可以被視為信息壓縮的不同形式。

設原始數據為隨機變量，聚類的目標是通過一個標籤變量使得最大化（互信息最大化），而降維的目標是找到一個連續映射，使得最大且的維度儘可能小。

因此，聚類可以看作離散化的信息壓縮，而降維則是連續化的信息壓縮。二者都試圖在“信息保留”與“複雜度降低”之間尋找平衡點。

6 從幾何角度的聯繫

若將數據集視為嵌入高維空間的點集，降維的目標是尋找一個低維流形，使得樣本點到的距離最小。而聚類的目標則是找到若干局部區域，使得樣本主要集中於其中。

在理想情形下，流形的局部結構與聚類劃分之間有對應關係：每個簇可能位於流形的某個連通分支上。也就是説，聚類是對降維流形結構的局部劃分。

7 應用層面比較

應用場景	聚類的作用	降維的作用
文本挖掘	文檔主題發現	詞向量壓縮
圖像識別	圖像類別劃分	特徵嵌入提取
生物信息	基因分型	基因表達降噪
客户分析	用户羣體分割	行為特徵提取
可視化	驗證聚類結果	展示全局結構

在大規模機器學習流程中，降維通常先於聚類執行，以提高算法穩定性與效率。例如在圖像特徵中，使用PCA可減少噪聲維度，再用K-Means對低維嵌入進行聚類，從而發現潛在模式。

8 總結與展望

聚類與降維分別從不同層面揭示數據的結構規律。聚類強調樣本間的羣體關係，降維強調特徵間的主導方向。它們的區別在於輸出形式與優化目標，而聯繫則體現在數學抽象、幾何結構與信息壓縮機制上的共通性。

在當前深度學習與自監督學習快速發展的背景下，聚類與降維的界限進一步模糊。表示學習模型（Representation Learning）往往同時兼具二者功能：通過嵌入空間學習實現降維，通過嵌入結構形成自然聚類。例如，Transformer模型在隱含層空間中學習到的分佈，本質上就隱含着聚類與降維的統一過程。

未來研究方向包括：

• 基於自適應流形的聯合優化模型；
• 動態聚類與流形演化分析；
• 在信息瓶頸理論框架下重新定義無監督結構學習。

這些方向將推動聚類與降維從方法論上的並列關係，走向理論層面的融合與統一。