在現代科學與工程領域中，數據預測已成為理論研究與實際應用的核心任務之一。隨着信息技術的發展，數據規模呈指數級增長，系統變量間的關係呈現高度非線性和複雜耦合特徵。傳統的線性迴歸或統計模型在面對高維、非線性以及噪聲干擾的數據時，往往難以提供穩定且高精度的預測結果。在這一背景下，支持向量機（Support Vector Machine, SVM）作為一種基於統計學習理論的算法，憑藉其數學嚴謹性和幾何直觀性，成為解決複雜預測問題的重要工具。

SVM最初被提出用於分類任務，其核心在於尋找一個能夠最大化間隔的分類超平面，從而保證模型在未知樣本上的泛化能力。然而，隨着理論的深入與方法的拓展，SVM逐漸被應用於連續數值預測任務，即支持向量迴歸（Support Vector Regression, SVR）。這種方法不僅能有效處理小樣本和高維數據，還能通過核函數捕捉數據的非線性關係，實現複雜系統的高精度預測。

在科學研究、金融市場、能源管理、工業控制等諸多領域，SVM的預測能力得到了廣泛驗證。其理論核心——結構風險最小化和最大間隔原理——使得模型在面對有限樣本時仍能保持對未知數據的穩定輸出能力。這種從分類到迴歸、從有限樣本到泛化預測的跨越，不僅體現了SVM方法論的普適性，也揭示了其在數據預測領域中潛在的深刻價值。

通過深入理解SVM的數學基礎、優化機制及核方法的作用，我們可以揭示其在數據預測中的核心驅動力，為構建高精度、魯棒性強的預測系統提供理論支撐與實踐指導。

一、SVM的理論基礎：結構風險最小化與統計學習原則

支持向量機的理論基礎植根於統計學習理論（Statistical Learning Theory, SLT），其核心目標是通過數學方法在有限樣本條件下實現對未知數據的可靠預測。SVM不同於傳統經驗風險最小化（Empirical Risk Minimization, ERM）方法，它採用結構風險最小化（Structural Risk Minimization, SRM）原則，從理論上提供了泛化能力保障。

（1）經驗風險與泛化能力

在機器學習中，模型的訓練目標通常是最小化訓練數據上的誤差，即經驗風險：

其中，表示預測函數與真實值之間的損失函數。經驗風險最小化通過優化訓練樣本上的誤差來構建模型，但在樣本有限或數據噪聲較高的情況下，模型可能出現過擬合，從而降低對未知樣本的預測能力。

結構風險最小化原則則在經驗風險的基礎上加入模型複雜度控制，通過在模型空間中選擇合適的假設集合來降低泛化誤差。SRM的目標可以形式化為：

其中，為真實風險，為對假設空間複雜度的度量，常用VC維（Vapnik-Chervonenkis Dimension）來量化。通過在有限樣本下控制的容量，SVM可以在保持訓練誤差較低的同時，實現對未知數據的穩定預測。

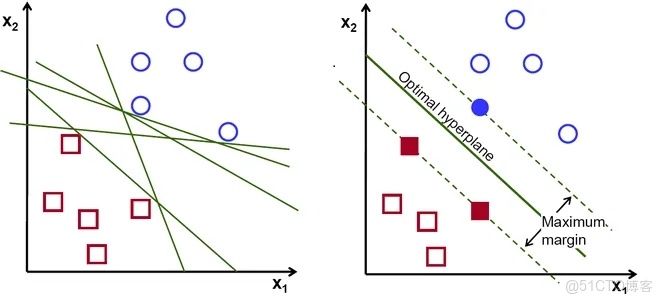
（2）最大間隔原理與幾何解釋

SVM的另一個理論支撐是最大間隔原理。在二分類問題中，假設訓練集為：

SVM的目標是尋找一個線性超平面：

使得兩類樣本被正確分類，同時最大化樣本到超平面的最小距離。定義分類間隔為：

通過最大化間隔，SVM不僅保證了分類的正確性，還增強了模型對未知樣本的泛化能力。該優化問題可表示為約束優化形式：

該凸二次規劃問題保證了全局最優解的唯一性，也提供了清晰的幾何解釋：支持向量是那些位於間隔邊界上的樣本，它們直接決定了最優超平面的位置。

二、核方法與非線性映射：擴展SVM的預測能力

儘管線性SVM在可分數據上效果顯著，但在現實預測問題中，數據通常呈現複雜的非線性關係。為此，SVM引入核函數（Kernel Function）實現高維映射，使得非線性問題在映射後的高維空間中變為線性可分。

（1）核函數的基本思想

通過核函數，SVM無需顯式計算高維映射，即可在高維空間中構建線性超平面。映射滿足：

常用核函數包括：

• 線性核：
• 多項式核：
• 徑向基函數核（RBF）：

核函數的選擇直接影響SVM在非線性預測中的擬合能力和泛化性能。例如，RBF核能捕捉複雜局部模式，而多項式核可反映全局非線性趨勢。

（2）對預測的意義

在數據預測任務中，核方法提供瞭如下功能：

1. 非線性關係建模：複雜系統變量之間的非線性耦合可以通過核映射線性化處理。
2. 高維特徵空間擴展：將低維輸入映射到高維特徵空間，增加模型表示能力。
3. 支持向量稀疏性保留：預測函數僅依賴支持向量，即誤差邊界上的樣本，保證計算效率。

在核方法作用下，SVM預測函數可表示為：

其中，表示支持向量集合，為拉格朗日乘子，為偏置項。該形式使得SVM在面對小樣本、高維非線性數據時仍能保持穩定且精確的預測能力。

（3）非線性預測問題示例

假設在時間序列預測中，序列數據受到前個時間點的影響：

通過核方法映射到高維空間，SVM能夠捕捉序列中隱含的非線性依賴關係，預測輸出為：

該預測機制避免了對序列線性假設的依賴，適應複雜動態系統的建模需求。

三、SVM的迴歸擴展：從分類到數值預測

（1）SVR（Support Vector Regression）的核心思想

支持向量機迴歸（SVR）是SVM在預測領域的主要形式。其核心思想是通過在高維空間中找到一個最優函數，使得預測值與真實值之間的偏差在允許範圍內最小化。其優化形式為：

約束條件為：

該優化目標試圖在最小化模型複雜度的同時，使預測誤差控制在範圍內。參數用於平衡預測誤差與模型平滑性。

最後的迴歸函數為：

其中，為拉格朗日乘子，僅對應於支持向量（即誤差超過的樣本）。因此，SVR的模型不僅稀疏、可解釋，而且在小樣本和高維場景下表現穩定。

（2）-不敏感損失函數

SVR使用的-不敏感損失函數定義為：

這種損失設計具有重要意義——它允許一定範圍內的有預測誤差（不懲罰），從而增強模型的容錯性與平滑性。這使得SVR在處理噪聲較多的數據時更加穩健，也能有效避免對局部異常點的過度擬合。

四、SVM在預測任務中的應用機制

（1）泛化能力的理論支撐

SVM的預測優勢源自其結構風險最小化原則。這一原則使得模型在面對未知樣本時能保持高精度預測。不同於神經網絡依賴大量參數的自由學習，SVM在有限樣本條件下通過對支持向量的精確約束建立預測函數，從而具有更高的泛化可靠性。

設有訓練樣本集和未知樣本，SVM的預測輸出為：

預測值依賴於與支持向量的相似度，而非整個數據集，從而在樣本規模擴展時保持計算穩定性。這一特徵對於實時預測系統尤為重要。

（2）時間序列預測中的SVM

在時間序列預測中，SVM常被用來捕捉非線性動態特徵。例如，對於一維時間序列，可以構造輸入向量，預測輸出為。通過SVR建模，可實現非線性映射：

這種方法在能源負荷、金融市場、交通流量、氣象預測等領域表現突出。與ARIMA等線性模型相比，SVM無需對數據分佈進行假設，也不依賴平穩性條件，而是通過核映射直接捕捉數據間的複雜關聯。

（3）多維數據預測

SVM不僅能預測單變量，還能擴展至多維數據預測。例如，在工業過程建模中，輸入變量可能包括温度、壓力、流量等多維特徵，輸出為產品性能指標。通過多維核映射，SVM能夠有效提取變量間的耦合關係，實現複雜系統的精準建模。

五、SVM在數據預測中的優勢與侷限

（1）主要優勢

1. 泛化能力強：通過結構風險最小化原理實現高精度預測。
2. 小樣本學習能力突出：在訓練樣本有限時仍能保持穩定性能。
3. 核函數的靈活性：可根據數據特性選擇不同核函數實現非線性映射。
4. 模型稀疏性：僅由支持向量決定預測函數，計算高效。
5. 對高維數據魯棒：不受維度詛咒的顯著影響。

（2）主要侷限

1. 參數選擇依賴經驗：核參數與懲罰係數需通過交叉驗證或網格搜索優化。
2. 大規模數據處理效率較低：在超大樣本時訓練時間增加明顯。
3. 模型可解釋性相對有限：雖然相比神經網絡更透明，但核空間映射的高維性使得直接解釋困難。
4. 對噪聲敏感性：在參數選擇不當時，模型可能對離羣點反應過強。

六、SVM預測的算法實現與優化策略

（1）訓練算法

SVM的求解問題是一個凸二次規劃問題。常用的優化方法包括：

• SMO算法（Sequential Minimal Optimization）：將大規模優化問題分解為多個二元子問題，逐步求解，效率高。
• 內點法（Interior Point Method）：通過構造勢函數逼近最優解，適用於中等規模數據。

在SVR中，SMO同樣被廣泛應用，以加快回歸模型的訓練速度。

（2）模型參數優化

核函數參數（如RBF核中的）與懲罰參數的選取對預測性能影響重大。常用優化策略包括：

• 網格搜索（Grid Search）
• 交叉驗證（Cross Validation）
• 貝葉斯優化（Bayesian Optimization）

通過在參數空間內系統搜索或智能採樣，可以獲得最優預測模型。

（3）混合預測模型

在實際應用中，SVM常與其他算法結合以提升性能。例如：

• SVM + PCA：通過主成分分析降維後再輸入SVM，提高效率；
• SVM + 粒子羣優化：利用羣體智能算法優化SVM參數；
• SVM + 神經網絡：結合深層特徵提取與SVM分類器，實現高維預測。

這些混合方法拓展了SVM的應用邊界，使其能適應複雜的預測任務。

七、SVM在典型預測場景中的案例分析

（1）金融市場預測

在股票價格或匯率預測中，SVM通過核函數捕捉非線性價格波動關係。輸入特徵可包括歷史價格、成交量、技術指標等。研究表明，基於SVM的預測模型在短期趨勢預測中優於傳統線性模型，特別是在波動性較高的市場條件下。

（2）能源負荷預測

電力系統的負荷預測是能源管理中的關鍵環節。SVR通過學習歷史負荷與天氣、時段等因素的關係，可在不同時間尺度上預測未來負荷。該模型的穩定性使其成為電力調度和供需平衡的重要工具。

（3）工業過程與質量控制

在複雜製造系統中，SVM可用於性能參數預測與故障檢測。通過對傳感器數據建模，SVM能夠對設備狀態進行早期預警，從而提高生產效率與可靠性。

八、總結

支持向量機從分類算法到預測模型的演化，是統計學習理論嚮應用智能擴展的重要體現。它通過最大間隔和結構風險最小化，實現了從離散決策到連續預測的跨越。在預測任務中，SVM所啓動的核心機制是泛化控制：在有限樣本上，通過最優間隔構造，使模型具備面向未知數據的穩定輸出能力。這種能力正是科學建模的關鍵所在。

SVM在預測中的價值，不僅在於其算法性能，更在於其思想深度：以幾何方式描述統計學習的邊界，以最優原理統一分類與迴歸的框架。這種理論與實踐的統一，構成了機器學習中最具啓發性的範式之一。

以下為專欄文章推薦

在當代科研與技術探索中，學術思維的深度與方法論的嚴謹性共同決定了研究工作的質量與前瞻性。研究不僅依賴於實驗與數據，還需要對理論框架、數學工具及其應用邏輯有全面的理解與掌握。首先，從科研方法與學術寫作角度來看，如何構建科學問題、選擇研究路徑以及提升論文講故事能力是每位科研工作者必須面對的核心問題（怎麼寫文獻綜述？如何找到重要問題？一個空白領域，如何開始研究？應該擁有哪些良好寫作習慣？如何提升科研論文講故事能力？論文寫作專欄）。這些問題不僅涉及文獻調研與研究方法，還要求研究者在撰寫過程中能夠清晰呈現問題背景、方法選擇與創新點的邏輯鏈條，從而增強科研成果的可理解性與學術影響力。

在機器學習與人工智能方向，模型構建與選擇的合理性直接影響學習效果與預測能力。無監督學習領域中，聚類算法、自動編碼器、生成模型以及PredNet模型各有不同的實現機制與適用場景（無監督學習四種實現模型（聚類學習、自動編碼器、生成模型、PredNet）之間的區別是什麼？VAE與GAN有何本質差異？）。例如，VAE通過概率生成模型實現潛空間分佈學習，而GAN則通過對抗訓練機制逼近目標分佈，這種本質差異決定了兩者在生成質量、訓練穩定性以及可解釋性上的不同表現。此外，在深度學習模型訓練過程中，經常會出現訓練集準確率接近100%，而驗證集準確率在80%附近波動的現象（訓練集準確率接近100%，驗證集準確率80%但隨着訓練step增加不增也不降。算是過擬合還是欠擬合？驗證集是不是沒有欠擬合説法？）。這提示我們需要仔細區分過擬合與欠擬合的定義，並結合訓練曲線、正則化手段以及數據分佈特徵進行綜合分析。

再從數學與優化理論上，理解矩陣運算、線性空間與對偶關係對於科研建模及算法設計具有基礎性意義（如何理解矩陣對矩陣求導？線性空間的對偶空間和優化裏的拉格朗日對偶有什麼關係？行列式的意義是什麼？如何解釋線性迴歸？上週專欄回顧）。矩陣對矩陣求導不僅是求解最優化問題的工具，也是深度學習反向傳播算法的核心計算單元；拉格朗日對偶則將約束優化問題轉化為對偶問題，為全局最優解分析提供理論保障。在實際應用中，行列式的幾何意義、線性迴歸參數估計的最小二乘性質都需要通過嚴密的線性代數和概率論方法進行解析。

概率論與統計學提供了科學推斷與不確定性量化的基礎。隨機變量的定義、離散與連續類型的區分、多維隨機變量的獨立性及聯合分佈關係，都是構建統計模型和解釋實驗結果的前提（如何理解隨機變量的定義？離散與連續隨機變量的核心差異在哪裏？獨立性與聯合分佈之間的關係如何表達？多維隨機變量獨立性如何嚴格定義？）。在高維數據分析和機器學習中，嚴格定義多維隨機變量的獨立性尤為重要，它不僅影響條件概率計算，還直接關係到模型可解釋性和泛化能力。

在自然語言處理與大模型領域，位置編碼機制是保持序列信息穩定性的關鍵因素。特別是RoPE位置編碼在超長上下文任務中，通過相位偏移實現注意力矩陣的穩定性，這體現了模型設計中對序列依賴性與計算穩定性的高度考慮（為什麼llm大模型主要都是用RoPE位置編碼而非其他？在超長上下文任務中，RoPE的相位偏移為何能保持注意力矩陣穩定？）。這一設計不僅優化了長序列信息保留，還在一定程度上減輕了梯度消失與注意力衰減問題，為構建可擴展大模型提供了理論依據與實踐方案。