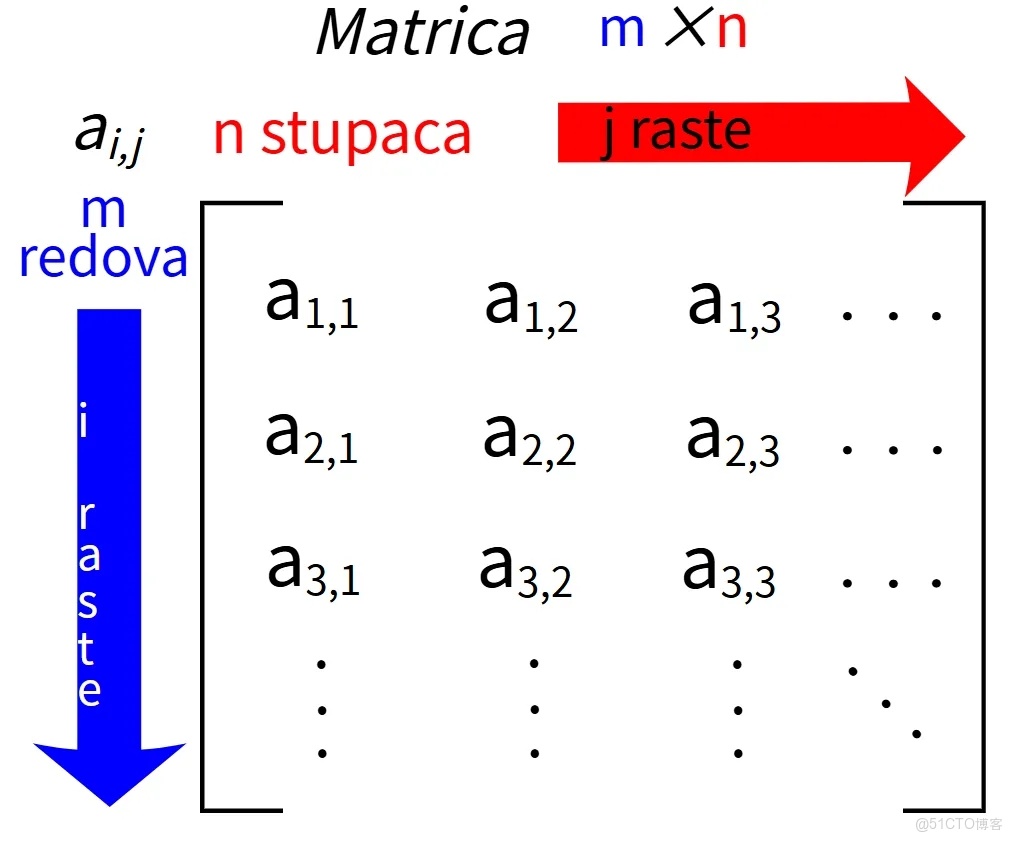
在線性代數的理論體系中，矩陣是描述線性映射和向量空間結構的核心工具。矩陣不僅用於描述有限維空間的變換，還廣泛應用於量子力學、統計力學、羣表示理論、微分幾何以及現代計算科學。在學習矩陣時，一個看似簡單的概念——矩陣的跡——經常被提及。

初次接觸跡的人可能會認為它只是矩陣對角線元素的求和：

然而，這種表面上的簡單掩蓋了其深層的數學與物理意義。跡不僅是線性代數中的數值運算，它反映了線性變換的全局特性、算子譜的代數和、以及與空間結構和幾何量相關的本質信息。

在物理理論中，跡體現了座標獨立性和整體平均性。例如在量子力學中，密度矩陣的歸一化條件和算符期望值的計算都依賴於跡操作，保證了理論結果與座標選擇無關。在微分幾何中，Jacobian矩陣的跡與向量場的散度密切相關，反映局部體積變化率。在統計和優化領域，跡衡量協方差結構、能量分佈或模型複雜度，是全局信息的濃縮表達。

由此可見，矩陣的跡遠非簡單的算術和。它在數學與物理多個分支中重複出現，成為理解線性變換整體效應、算符性質和系統統計特徵的關鍵工具。其普適性和核心價值不僅體現在計算的便利性上，更在於其所捕捉的線性結構與整體行為的內在聯繫。

探討矩陣的跡，實際上是探討如何從代數形式提煉出線性變換的整體性質，如何從局部元素推演出系統全局特徵，這一問題貫穿數學、物理與計算科學的多個領域，也是理解線性算子深層次本質的關鍵起點。

一、跡的代數定義與基本性質

矩陣的跡最初被定義於有限維向量空間上的線性算子。設為一個矩陣，其跡定義為：

這一定義看似簡單，但在代數上具有深遠意義。它不僅是一種對角元素的求和操作，更是線性算子整體性質的量化指標。跡的定義滿足一系列重要性質，這些性質在高階數學和物理應用中起到基礎性作用。

1. 線性性

跡是線性泛函，這意味着對於任意兩個矩陣和標量，有：

這一性質確保了跡運算可與矩陣的線性組合相互兼容，在處理矩陣代數、優化問題或量子算符求期望值時，能夠直接將線性操作與跡操作結合使用。

2. 循環不變性

跡滿足循環不變性，對於任意可乘矩陣，有：

更一般地，對於個矩陣，可得：

這一性質在量子力學算符計算、張量收縮以及羣表示理論中具有重要意義。它表明跡對矩陣乘積中的“循環排列”不敏感，從而成為座標無關的全局量。

3. 相似不變性

若與相似，即有可逆矩陣使得，則跡保持不變：

相似變換對應於基底的更換，這意味着跡是線性算子的一個基底獨立的量。在代數上，它使跡成為線性算子的自然不變量，是描述算子本質特徵的重要工具。

4. 與特徵值的關係

若矩陣的特徵值為，則跡等於特徵值之和：

特徵值通常描述矩陣沿不同方向的伸縮效應，而跡的求和操作則提供了一個整體量度，反映了線性變換在所有方向上的總“代數效應”。因此，跡不僅是代數運算結果，也是譜信息的濃縮表達。

5. 與行列式的關係

跡與行列式共同描述矩陣的代數結構。對於矩陣，其特徵多項式為：

其中，跡出現在特徵多項式的次高次項的係數上，表明它是“第一譜不變量”，而行列式是“最後譜不變量”。這反映了跡與行列式在譜信息提取上的互補作用：跡描述代數和，行列式描述代數積。

二、跡的幾何解釋：線性變換的“平均效應”

從幾何角度看，跡可以被解釋為線性變換對空間的整體伸縮效應的度量。設為線性映射，對應矩陣。對於標準基向量，有：

其中表示在自身方向上的伸縮係數。跡即：

可視為所有基向量沿自身方向的線性效應的代數總和。它提供了對線性映射的全局幾何概覽，而非單一方向的信息。

1. 散度的聯繫

若表示某向量場的Jacobian矩陣：

則：

這表明跡在微分幾何中對應於向量場的散度，反映局部空間的體積變化率。換言之，跡度量了線性變換在局部對空間體積的影響，是幾何性質與代數運算之間的連接。

2. 體積變換與Jacobian

對於一個可逆線性變換，其對單位立方體的體積變換可以用行列式表示，而跡描述的則是變換在每個方向的“平均拉伸”，因此：

• 行列式提供總體體積變化
• 跡提供平均方向伸縮

在多維空間中，這種區分尤其重要。在動力系統分析中，Jacobian矩陣的跡與系統的李雅普諾夫指數密切相關，直接影響系統穩定性分析。

三、跡與特徵值的代數聯繫

跡與特徵值的關係揭示了其代數本質。設矩陣的特徵值為，則：

這一結論不僅説明跡與譜密切相關，還使跡成為研究譜性質的重要工具。

若考慮特徵多項式：

其係數與跡相關。例如：

跡作為係數出現在最高次項之後，代表了特徵值的“平均量”。這也是跡被稱為“第一譜不變量”的原因。

在羣表示理論中，這種聯繫更為顯著。羣的每一個表示可由一個矩陣羣實現，而跡（稱為角色函數）決定了表示的等價類：

角色函數的相等意味着表示的等價性，因此跡在表示理論中成為分類工具。跡的代數功能因此延伸至羣結構分析與不變量理論。

四、跡在算子理論中的推廣

在無限維空間中，跡的概念仍可推廣，但要求更嚴格。一個算子若為跡類算子（trace-class operator），則定義：

其中為任意正交基。與有限維情況一樣，跡與基的選擇無關。

跡類算子構成希爾伯特空間上極為重要的一類緊算子。它們使得“跡”這一有限維定義在分析框架中得以延續。例如，量子力學中密度矩陣的歸一化條件：

即表明系統的總概率為1。而期望值計算也依賴跡：

此處的跡運算確保物理量計算與座標無關，體現了統計平均的算符形式。

在泛函分析中，跡還出現在熱核展開與譜幾何中。例如，熱核的對角積分：

揭示了跡與譜之間的關係——它與特徵值分佈直接相關，從而建立了幾何與譜的聯繫。

五、跡在物理學中的深層角色

在物理學中，跡常用於構建具有座標獨立性和整體意義的量。跡的出現標誌着理論中所關心的量不依賴具體座標系，而與系統的總體態相關。

1. 量子力學中的跡 密度矩陣描述量子態，跡為其歸一化條件：
   
   物理可觀測量的期望值由跡表達：
   
   跡在此起到“加權平均”的功能，將算符形式的物理量轉化為可觀測標量。
2. 量子場論中的跡 在路徑積分與費曼圖計算中，跡用於求和自旋、顏色等內部自由度。例如在QCD中：
   
   跡確保羣結構的約化與規範對稱性的一致性。
3. 統計力學中的跡 配分函數定義為：
   
   其中為哈密頓算符。跡將能譜加權求和，從而得到系統的熱力學性質。無論系統的基底如何選擇，跡保證結果的物理一致性。

因此，跡在物理學中不僅是數學操作，更是“座標不變性”與“全系統平均”思想的體現。

六、跡在機器學習與優化中的應用

在現代計算科學中，跡廣泛出現在矩陣優化與深度學習模型的正則化項中。常見形式有：

此類項常出現在目標函數中，反映模型複雜度、協方差結構或能量分佈。

例如，在主成分分析（PCA）中，最大化數據協方差矩陣的跡即意味着最大化投影方差：

跡在此發揮“整體方差量化”的作用。

在核方法中，跡範數（nuclear norm）：

是矩陣秩的凸近似，被廣泛用於矩陣補全與低秩約束優化。跡在此體現出對結構複雜度的全局控制能力。

七、跡與循環結構：代數拓撲與張量分析的延伸

跡的循環不變性：

在張量代數中對應於指標的閉合。若我們寫作：

跡操作相當於“收縮”指標。它是一種把高階結構“閉合”為標量的方式。這種“循環閉合”的思想貫穿於代數拓撲與物理中的環結構分析。

在羣代數中，跡的不變性還導致了角色正交關係，這為不可約表示的分類提供了數學基礎。而在張量網絡、量子信息與廣義相對論張量運算中，跡操作常用以描述系統內部的“糾纏強度”或“信息封閉”。

八、跡的譜幾何意義與熱核展開

跡不僅與代數和線性算子有關，更與空間的幾何形態緊密相關。通過熱核跡：

可以從譜信息中重建幾何特徵。著名的“聽形狀的鼓”問題（Can one hear the shape of a drum?）即研究如何通過拉普拉斯算子的譜（從而通過跡）推斷幾何形態。

當時，熱核跡的漸近展開為：

其中係數包含空間的曲率、維度等幾何信息。由此，跡成為連接幾何與譜的紐結。

九、跡的抽象化與範疇論視角

在更高層的抽象中，跡被推廣到範疇論框架中。對於一個對稱單oidal範疇中的自同態，可定義“範疇跡”。它捕捉了對象自映射的內在結構，與矩陣跡在概念上等價。

這一觀點揭示了跡的本質——它是對自映射的“全局自作用的收縮”運算。這種抽象使跡成為數學多個分支中共享的概念核心。

十、結論

跡是線性代數中最簡單卻最深刻的算子之一。它的意義不僅僅在於數值計算，更在於它揭示出一個結構性事實：任何線性變換都可以通過跡捕捉其全局的“代數平均效應”。

跡統一了代數、幾何、分析與物理的視角：

• 在代數中，它反映譜性質；
• 在幾何中，它代表局部體積變化率；
• 在物理中，它實現全系統的統計平均；
• 在分析中，它連接譜與空間結構；
• 在優化中，它衡量複雜度與能量分佈。

它之所以如此普適，正因為跡所表達的，是關於系統整體結構的度量，而非局部的細節。跡的思想，是“從整體看變換”的思想。