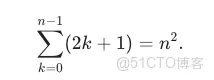我之前説過講一下math V2的論文，今天來還個願

      其實為什麼這論文沒人重視呢？主要是兩個原因：

      1- 絕大多數人討厭數學

      2- 之前出過一個prover2，大家也不知道幹啥的也和數學有關，然後又來一個

      討厭數學就不説了（甚至有人討厭香菜），主要説第二個，prove2為什麼讓人不知道是幹啥的？

      它其實是lean 生成器，你一定會問什麼是lean，現在都是lean4

      lean4 是 MS Research 開發的交互式定理證明器，一種函數式編程語言 + 數學驗證工具，實在理解不了你就當他是python就完了，但是主要for 數學定理證明

     比如：     

    傳統數學：寫證明如散文“顯然由勾股定理所示，巴拉巴拉...”，人類讀懂（小學就這麼教的），但電腦無法“驗證”每步是否嚴謹（它不理解）。

    Lean 形式化：一切寫成代碼，電腦逐行編譯/驗證。證明 = 可執行程序，零歧義、機器查證      

     傳統證明像“手寫作文”（主觀，比如你高考答最後幾道大題的時候），Lean 像“Python 代碼 + 測試用例”（運行即驗）   

     Deepseek為什麼要玩 Lean呢？

• 數學家用它形式化數論/幾何定理（已形式化 10萬+ 定理的 Mathlib 庫），所以你有可以證明的dataset了麼
• AI 數學增強：生成 Lean 代碼， Lean 運行驗證 ，證明成功/失敗因為有了binary的 feedback，可以完美 RL 獎勵閉環。
• Prover-V2 專為 Lean 優化 tokenizer，支持 theorem、by、sorry 等語法。現在可以生成也能看懂lean代碼了

舉個例子：

比如我們要算一個定理，前 n 個奇數的和等於 n^2：

這個對應lean聲明（formal state）就是

import Mathlib.Data.Nat.Basic
import Mathlib.Algebra.BigOperators.Basic


open BigOperators


/--
The sum of the first `n` odd numbers equals `n^2`:
`∑_{k = 0}^{n-1} (2k+1) = n^2`.
-/
theorem odd_sum_square (n : ℕ) :
    ∑ k in Finset.range n, (2 * k + 1) = n ^ 2 := by
  -- proof to be filled
  admit

然後把這個東西改成prompts發給prover2裏的V3（prover2是兩個模型組成的一個V3，一個7B的子處理器）

V3接到一個這樣的prompts

[System] You are a mathematical reasoning expert and Lean 4 proof designer.
Given a math problem and its Lean formal statement, you should:


1. Explain the solution in natural language (chain-of-thought).
2. Decompose the proof into clear subgoals.
3. Produce a Lean 4 proof skeleton which follows your plan and
   contains `sorry` placeholders for subgoals.


[User]
Problem (informal):
Prove that the sum of the first n odd numbers equals n^2.


Formal statement (Lean 4):
theorem odd_sum_square (n : ℕ) :
  ∑ k in Finset.range n, (2 * k + 1) = n ^ 2 := by
  ?_

處理完了，就成了一個COT的解題的視角+lean的骨架了，緊緊差一些細節的subgoal沒去證明

[DeepSeek-V3]


(1) Natural-language chain-of-thought (high-level plan):


We prove by induction on n.


Base case: n = 0. The sum over an empty range is 0, and 0^2 = 0.


Inductive step: assume that for some n we have
  ∑_{k < n} (2k + 1) = n^2.
Then
  ∑_{k < n+1} (2k + 1)
= (∑_{k < n} (2k + 1)) + (2n + 1)
= n^2 + (2n + 1)
= (n + 1)^2.
Thus, by induction, the equality holds for all n.


(2) Subgoal decomposition (informal):


Subgoal 1 (base case):
  Show: ∑_{k < 0} (2k+1) = 0^2.


Subgoal 2 (range decomposition):
  For all n,
  ∑_{k < n+1} (2k+1) = (∑_{k < n} (2k+1)) + (2n+1).


Subgoal 3 (inductive hypothesis usage):
  Assume IH: ∑_{k < n} (2k+1) = n^2.
  Show: ∑_{k < n+1} (2k+1) = (n+1)^2.


Subgoal 4 (algebraic identity):
  Show: n^2 + (2n+1) = (n+1)^2.


(3) Lean 4 proof skeleton with `sorry`:


import Mathlib.Data.Nat.Basic
import Mathlib.Algebra.BigOperators.Basic


open BigOperators


theorem odd_sum_square (n : ℕ) :
    ∑ k in Finset.range n, (2 * k + 1) = n ^ 2 := by
  -- induction on n
  induction' n with n ih
  · -- Subgoal 1: base case n = 0
    -- ∑_{k < 0} (2k+1) = 0^2
    -- (use simp to evaluate the empty sum)
    sorry
  · -- Subgoal 2 + 3 + 4: inductive step
    -- We rewrite the sum over `range n.succ`.
    have h_decompose :
        ∑ k in Finset.range n.succ, (2 * k + 1)
          = (∑ k in Finset.range n, (2 * k + 1)) + (2 * n + 1) := by
      -- Subgoal 2: range decomposition
      sorry


    -- Use the induction hypothesis to replace the partial sum by n^2.
    have h_using_IH :
        (∑ k in Finset.range n, (2 * k + 1)) + (2 * n + 1)
          = n ^ 2 + (2 * n + 1) := by
      -- Subgoal 3: apply IH
      sorry


    -- Now prove the algebraic identity n^2 + (2n+1) = (n+1)^2.
    have h_algebra :
        n ^ 2 + (2 * n + 1) = (Nat.succ n) ^ 2 := by
      -- Subgoal 4: algebraic manipulation
      sorry


    -- Combine the equalities to close the goal.
    -- target: ∑_{k < n.succ} (2k+1) = (n.succ)^2
    -- by transitivity using h_decompose, h_using_IH, h_algebra
    sorry

下面open Bigoperators的就是lean4的基本骨架了，然後每一個-- 是一個subgoal，sorry留着當佔位符，交給7b的小模型去證明了

舉一個子目標的例子：

[System] You are a Lean 4 theorem prover. Your task is to fill in the proof
of the given lemma, without changing its statement.


[User]
Context:


import Mathlib.Data.Nat.Basic
import Mathlib.Algebra.BigOperators.Basic


open BigOperators


-- `odd_sum_square` is being proved by induction on `n`.
-- In the inductive step, we have the following subgoal:


theorem range_decompose_subgoal (n : ℕ) :
    ∑ k in Finset.range n.succ, (2 * k + 1) =
      (∑ k in Finset.range n, (2 * k + 1)) + (2 * n + 1) := by
  ?_


Please fill in the proof in Lean 4.

7B的就把這個給解了，解完之後的被帶入到原來的V3的結果了，sorry被替換成這個結果

[Prover-7B]


theorem range_decompose_subgoal (n : ℕ) :
    ∑ k in Finset.range n.succ, (2 * k + 1) =
      (∑ k in Finset.range n, (2 * k + 1)) + (2 * n + 1) := by
  -- Use the standard lemma `Finset.range_succ`.
  -- It tells us:
  --   range (n.succ) = range n ∪ {n},
  -- and the sum over `range (n.succ)` splits accordingly.
  simpa [Finset.range_succ, Nat.succ_eq_add_one] using
    Finset.sum_range_succ (fun k => (2 * k + 1 : ℕ)) n

每個subgoal都被解完，那麼自然就出了一個完整的lean證明，交給lean verify去驗證就可以了

所以prover-v2再解答數學題的時候是這個套路，大家看懂了嗎？

--------------沒看懂沒關係，反正你們也用不到-------------

下面講容易理解的math-v2

mathV2 就特別的好理解，但是很天才的設計

比如標準V3也能做數學題，但是做不了證明題，因為大模型對數學題的做法和人腦考慮不一樣，所以之前訓了prove2，拿lean來做驗證

大家經常能看到一個數學題給LLM，它結果正確，但是中間的think步驟都在亂寫

為什麼這樣？

因為你grpo也好，ppo也好，你都確認的是最終答案的值

有人説你的不對，因為R1論文裏寫的，grpo同樣對think的中間過程check，check是check，只是check你輸出的範式是不是<think></think>

那麼prm是不是個好的思路，但是prm難訓啊。

Deepseek math V2的做法是什麼？

其實可以總結為抽象PRM

不同於每一步都要驗證正確與否的PRM，你針對輸出中間結果統一確認個好壞，這個還是可以實現的吧！

所以思路就來了

首先，我要有一個小鎮做題家，一個給做題家批卷子的老師，但是這個老師可能本身就不咋滴，所以我還要找個教委的來監督老師的水平。

於是就有了下面這3個模型

1. 證明生成器 ，做題家(Proof Generator) (πθ)

這是負責實際生成數學證明的語言模型。

• 功能： 根據給定的問題 (X) 生成證明 (Y)。

• 訓練目標： 使用訓練好的驗證器作為獎勵模型 (RY) 對其進行強化學習訓練，以最大化證明質量。

• 自我驗證： 為了增強推理能力，生成器還被激勵產生證明 Y 之後，緊接着進行自我分析 (Z)，即自我評估和糾錯。這種自我評估的準確性也受到獎勵，簡單説就是你想高考取得高分，光做選擇題和填空是不行的，你得做大題證明題，而且你的證明步驟得寫清楚，這部分會有額外的分數。

2. 證明驗證器 ，判卷老師(Proof Verifier) (πϕ)

這是負責評估證明質量的核心組件。

• 功能： 根據高層評估標準 (Iv)，評估證明的完整性和嚴謹性，並給出分數（1 分、0.5 分或 0 分）。

• 作用： 它作為獎勵模型，為證明生成器提供反饋，指導其優化。

• 訓練基礎： 它最初是在一個經過監督微調的模型 (DeepSeek-V3.2-Exp-SFT) 的基礎上，通過強化學習進行訓練的。

3. 元驗證器 ，教委的監督人員(Meta-Verifier) (πη)

這是一個專門用於確保驗證器本身的分析結果忠實可靠的輔助模型。

• 動機： 作者引入元驗證是為了解決驗證器可能在評分正確的情況下，“虛構不存在的問題” 以獲得滿獎勵的漏洞。

• 功能： 元驗證器被訓練來評估驗證器輸出的分析 (V) 的質量。它會檢查驗證器指出的問題是否真實存在，以及這些問題是否在邏輯上支持驗證器給出的分數。就是你老師寫的評語是否靠譜。

• 協同作用： 元驗證器提供的質量分數 (Rmeta) 被整合到證明驗證器的獎勵函數中，從而提高了驗證器在識別問題方面的忠實性（faithfulness）

這裏其實隱藏了一個邏輯，教委憑什麼能給老師的判卷評語打分，他知識能力一定比老師強嗎？也就是元驗證器一定比驗證器厲害嗎？

   非也，因為他倆做的不是一個任務，老師給學生打分，是非常複雜的，它要確認它確實看懂了學生的對與錯，問題到底出在哪？要寫出很詳實的證明。

   但是，對於老師給題打的分數對應的評語，教委的邏輯是很簡單的，就像讓你做題你做不出來，但是讓你給別人的論調裏挑錯，你又積極，又能找出問題所在，一旦元驗證（教委的能力）發現老師這評語都開始亂寫了，那麼就到了升級老師的時候。

現在3個role都到位了，開始做題

做題家做了一道題---> 老師不光看你做對沒有，還要看你的中間過程，然後從答案的正確性，和中間過程的正確性兩個維度給你做題家打分----> 答案一般是有唯一的，但是中間過程未必是唯一的，怎麼能證明老師公平公正的給做題家打分，教委（元驗證器）就來檢查老師的評語來了。

那麼要實現這樣一個做題到打分流程，怎麼訓練呢？

詳細過程：

1. 證明驗證器 (πϕ) 的訓練和增強

作為老師（PRM，雖然是all process的rm），證明驗證器 (πϕ) 是整個系統的核心，因為它定義了獎勵函數和證明質量標準。

初步訓練

1）. 基礎模型： 驗證器是基於 DeepSeek-V3.2-Exp-SFT 版本訓練的，該版本經過監督微調（SFT）處理，擁有與數學和代碼相關的推理數據基礎。

2）. 數據構建： 研究人員首先從 AoPS 競賽中抓取了 17,503 個主要需要證明的數學奧賽問題 (Dp)。

3）. 生成和標註： 光有Dp這點東西不夠用啊，隨後，使用DeepSeek-V3.2-Exp-Thinking （這個模型我好像沒見過他們發啊）生成了候選證明，並提示該模型進行多輪迭代優化以提高全面性和嚴謹性。然後就當上人拉肩扛了，沒辦法冷啓動是這樣的，找一堆數學專家根據預定義的高級評估標準 (Iv) 對這些證明進行評分（1 分、0.5 分、0 分），從而構建了初始的 RL 數據集 Dv。

4）. RL 目標： 驗證器通過強化學習進行訓練，目標是生成證明分析並給出分數。獎勵函數包括有格式獎勵 (Rformat): 確保輸出包含識別出的問題總結和分數，另外分數獎勵 (Rscore): 基於預測分數 (s′) 與專家標註分數 (s) 的接近程度 (1−∣s′−s∣) 來獎勵模型。

搞定了老師以後，引入教委的監督元驗證器 (πη) 提高忠實性

元驗證器 (πη) 登場：初步訓練存在一個關鍵漏洞：當老師證明存在缺陷 (si<1) 時，驗證器可以通過預測正確的低分數來獲得滿獎勵，但同時虛構出不存在的問題（hallucinating non-existent issues），多少有點獎勵黑客（可能叫獎勵乞丐更合適），從而損害了它的可信度。為了解決一問題，引入了元驗證器 (πη)。它是一個獨立的、經過 RL 訓練的模型，用於評估驗證器分析本身的質量，而不是評估原始證明的質量。

元驗證訓練： 專家根據元驗證標準 (Imv) 對初始驗證器產生的分析 (Vi) 進行評分 (msi∈{0,0.5,1})，生成 Dmv 數據集。元驗證器通過 RL 訓練，其目標是評估驗證器指出的問題是否確實存在以及這些問題是否邏輯上支持驗證器給出的分數。

增強驗證器： 最終（在某個訓練的checkpoint裏，論文沒説這塊），元驗證器提供的質量分數 (Rmeta) 被整合到證明驗證器的獎勵函數中：RV=Rformat⋅Rscore⋅Rmeta。這提升了驗證器識別問題時的忠實性。經過增強，驗證器在驗證集上的平均分析質量分數從 0.85 提高到 0.96。

所以也可以理解，元驗證器在訓練初是存在的，在訓練中它的元驗證能力就被驗證器給吸納了（老師和教委合體了）

2. 做題家證明生成器 (πθ) 的訓練和自我驗證

初步訓練

• 初始化： 在每個訓練迭代中，證明生成器都是從驗證器的檢查點初始化的。比較諷刺的是，第一代學生做題家，其實是個老師。。。

• RL 目標： 生成器使用訓練好的驗證器 (πϕ) 作為獎勵模型。生成器的 RL 目標是最大化驗證器對所生成證明 (Yi) 給出的分數 (RY)。

增強推理能力的自我驗證

對於 IMO 和 CMO 等挑戰性問題，單次嘗試很難生成完美的證明。為了讓生成器具備迭代改進的能力，它被賦予了自我驗證的能力。

1）. 自我分析要求： 訓練時，生成器被要求在生成證明 (Y) 之後，立即生成一個遵循驗證器相同格式和標準 (Iv) 的自我分析 (Z)。

2）. 聯合獎勵結構： 獎勵函數結合了對證明本身的評分 (RY) 和對自我分析的元驗證分數 (RZ)。

◦ RY=s（驗證器給出的證明分數）   

◦ RZ=Rscore(s′,s)⋅Rmeta(Z)（s′ 是生成器預測的自我分數，s 是驗證器給的實際分數，Rmeta(Z) 是驗證器對自我分析忠實度的評估）。

3）. 激勵機制： 這種結構激勵模型做到以下幾點：

    ◦ 忠實地承認錯誤，而不是虛假地宣稱正確。

    ◦ 通過生成正確的證明並準確地認識到其嚴謹性來獲得最高獎勵。

    ◦ 生成器獲得高獎勵的有效策略是：在最終確定輸出之前，識別並解決自身證明中儘可能多的問題。

3. 驗證與生成之間的協同循環

驗證器和生成器（也帶着元驗證能力的）通過一個良性循環持續互相提升，這個循環中的關鍵是自動化標籤流程，它使得系統能夠在沒有人工干預的情況下擴展數據。

1. 協同效應：

 驗證器提高了生成器的能力，而更強大的生成器則產生了新的、更具挑戰性的證明，這些證明挑戰了驗證器當前的極限，即生成器與驗證器之間的差距，説白了驗證器整不好就看不太明白生成器再説啥了

。

2. 自動化標籤流程： 但是也不能因為看不懂就再來一次人拉肩扛吧？為了持續改進驗證器以適應這些新的、難以驗證的證明，deepseek開發了一個自動化標籤流程，該流程取代了人工標註。

    ◦ 步驟 1： 對每個新的證明，生成 n 個獨立的驗證分析，為啥要這麼幹呢？

最大化錯誤發現： 通過多次採樣，即使證明的缺陷非常細微或隱蔽，其中至少一個分析報告識別出該缺陷的可能性也會大大增加。

為元驗證提供依據： 只有那些在多次分析中報告問題的證明，才會被送入下一步的元驗證評估。這確保了只有最有可能包含缺陷的證明，才會進行更深入、更高質量的審查。

確定最低分數： 最終的標籤分配流程是檢查那些分配最低分數的分析。如果多個獨立的分析都報告了相同或相似的問題（即低分），那麼這個證據就更可靠，隨後元驗證會確認其有效

    ◦ 步驟 2： 對於報告問題的分析（分數 0 或 0.5），生成 m 個元驗證評估來驗證發現的問題是否有效。

    ◦ 步驟 3： 與此同時，如果大多數元驗證評估確認了問題，則該分析被認為是有效的。

    ◦ 步驟 4： 那麼，如果所有驗證嘗試中都沒有發現合理的問題，則證明被標記為 1 分；否則，證明被標記為有效分析中給出的最低分數。

     1分的（也可能早期會把0.5分一起）這些證明因為元驗證被標識為驗證你的證明是可信的，因為驗證你的證明是可信的，所以你的證明過程是可信的，那麼，做題家也就是生成器的證明邏輯本身就可以成為一條dataset被加入到下一輪train的datasets裏面，這個就是自動標籤的邏輯。

     這種全自動化流程在最後兩次訓練迭代中完全取代了人工標註，實現了在驗證計算規模擴大下，持續為驗證器創建新的訓練數據，從而進一步改進驗證器，因為生成器是驗證器的兒子，所以生成器也越來越厲害，生成器生成的數據被自動標籤流成給送到驗證器去了，驗證器又強了，強了以後又是下一個迭代的更厲害的生成器了，循環往復。

     這個比prover的影響大的原因，prover是特定領域機器對機器的對話（lean），本質上面太窄，但是基於自然語言驗證的數學就不一樣了，如果你能拿這個方法，做數學題能拿到IMO的金牌，那你玩代碼一樣可以用相同的方法拿到live bench的理論滿分，因為現在的vibe coding的一大問題是，思考範式比較差，只追求最初的邏輯勉強被滿足，然後瞎寫好多亂髮散的次優代碼，整體質量比較差，如果你的中間步驟都能特別的容易被證明，被元證明，那理論上你就能寫出和高級程序員一樣清晰又簡潔的代碼（不memory等需要解決的長尾效應的前提下）