一、理解信息論
想象一下這樣的場景,我們每天出門都會查看天氣預報,如果預報總是説"今天晴,氣温25度",久而久之你會覺得這信息索然無味,因為太確定了。但如果預報説"今天有80%概率下雨",我們就會格外留意,甚至帶傘出門,這種不確定性反而讓信息更有價值。
這正是信息論的精髓所在,就像收拾行李箱時,把所有物品整齊分類(低熵)比胡亂塞進去(高熵)更容易找到想要的東西。在大語言模型的世界裏,我們同樣在用這些原理,用“交叉熵”衡量模型預測的準確度,用“温度參數”控制回答的創造性,讓AI既能給出專業解答,又不失人性化的靈活。
今天,就讓我們一起探索這些看似抽象的概念,如何成為驅動人工智能的隱形引擎。
二、信息論對AI重要程度
AI和我們也很相似,也是一個長期學習和積累的過程,正如我們第一次看見一些動物,比如第一次看見貓,我們學習了貓這個概念,後面隨着看到的貓越來越多,我們逐漸對貓的理解越來越清晰。這個過程本質上就是信息傳遞和學習的過程。
在人工智能領域,特別是大語言模型中,我們面臨着類似的問題:
- 如何衡量一段文本的"信息含量"?
- 如何評估模型預測的"不確定性"?
- 如何比較不同概率分佈之間的"差異"?
這些問題的數學基礎都建立在信息論之上,信息論不僅是通信領域的基石,更是現代人工智能的核心數學工具。今天,我們一步步理解信息論的核心概念,並展示它們如何在大模型中發揮關鍵作用。
三、信息論基礎概念
1. 信息量
1.1 基本概念
信息量衡量一個事件發生的驚訝程度,事件越不可能發生,發生時帶來的信息量越大。
數學定義:
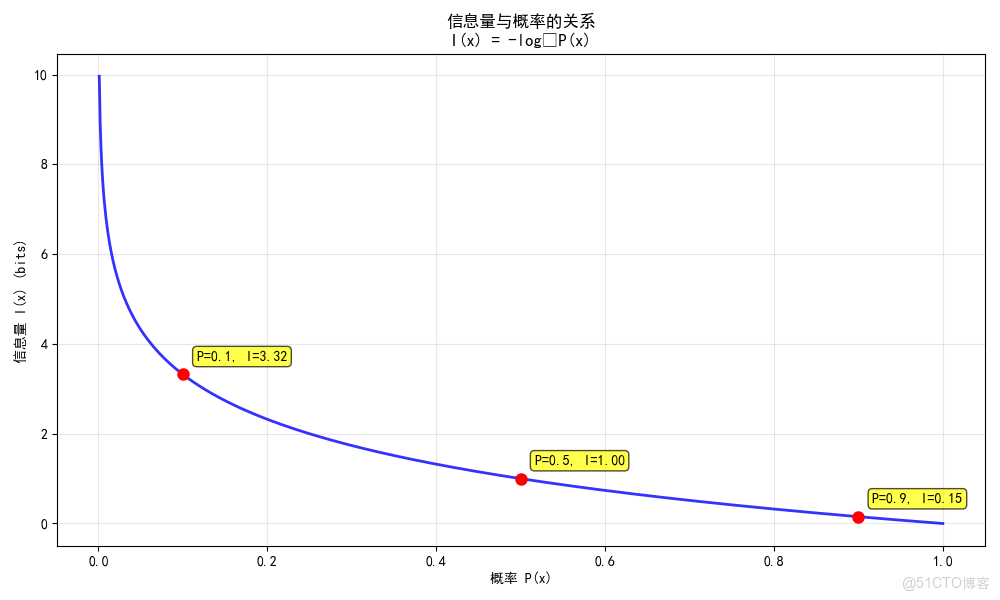
I(x) = -log₂ P(x)
參數説明:
- I(x):事件x的信息量(單位:比特)
- P(x):事件x發生的概率
- log₂:以2為底的對數
1.2 直觀理解
想象以下場景:
- "太陽從東邊升起":概率≈1,信息量≈0
- "今天會下雨":概率中等,信息量中等
- "贏得彩票":概率極小,信息量巨大
1.3 代碼實現
# 環境設置和庫導入
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from collections import Counter
import math
from scipy.special import entr
import warnings
warnings.filterwarnings('ignore')
# 設置中文字體(如果遇到顯示問題可以註釋掉)
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def information_content(probability):
"""
計算單個事件的信息量
Parameters:
probability: 事件發生的概率,範圍[0,1]
Returns:
information: 信息量(比特)
"""
if probability == 0:
return float('inf') # 不可能事件的信息量為無窮大
return -math.log2(probability)
# 示例計算
print("=== 信息量計算示例 ===")
events = [
("太陽從東邊升起", 0.999),
("今天會下雨", 0.3),
("贏得彩票", 0.0000001),
("拋硬幣正面朝上", 0.5)
]
for event_name, prob in events:
info = information_content(prob)
print(f"事件: {event_name:20} 概率: {prob:8.6f} 信息量: {info:8.2f} bits")
# 可視化信息量與概率的關係
probabilities = np.linspace(0.001, 1.0, 1000)
information_values = [information_content(p) for p in probabilities]
plt.figure(figsize=(10, 6))
plt.plot(probabilities, information_values, 'b-', linewidth=2, alpha=0.8)
plt.xlabel('概率 P(x)')
plt.ylabel('信息量 I(x) (bits)')
plt.title('信息量與概率的關係\nI(x) = -log₂P(x)')
plt.grid(True, alpha=0.3)
# 標記關鍵點
key_points = [0.1, 0.5, 0.9]
for p in key_points:
info = information_content(p)
plt.plot(p, info, 'ro', markersize=8)
plt.annotate(f'P={p}, I={info:.2f}', (p, info),
xytext=(10, 10), textcoords='offset points',
bbox=dict(boxstyle='round,pad=0.3', facecolor='yellow', alpha=0.7))
plt.tight_layout()
plt.show()
輸出結果:
=== 信息量計算示例 ===
事件: 太陽從東邊升起 概率: 0.999000 信息量: 0.00 bits
事件: 今天會下雨 概率: 0.300000 信息量: 1.74 bits
事件: 贏得彩票 概率: 0.000000 信息量: Infinity bits
事件: 拋硬幣正面朝上 概率: 0.500000 信息量: 1.00 bits
1.4 在大模型中的應用
在大語言模型中,信息量概念用於:
- 罕見詞檢測:罕見詞比常見詞攜帶更多信息
- 注意力機制:高信息量的詞獲得更多注意力
- 文本重要性評估:信息量大的句子對文檔理解更重要
2. 信息熵
2.1 基本概念
信息熵衡量整個概率分佈的"平均不確定性"或"混亂程度",是所有可能事件信息量的期望值。
數學定義:
H(X) = -Σ P(x_i) * log₂ P(x_i)
參數説明:
- H(X):隨機變量X的信息熵
- P(x_i):事件x_i發生的概率
- Σ:對所有可能事件求和
- log₂:以2為底的對數
2.2 熵的性質
- 非負性:H(X) > 0
- 確定性:當某個P(x_i)=1時,H(X)=0
- 極值性:均勻分佈時熵最大,H(X) ≤ log₂ P(x_i)
- 可加性:獨立隨機變量的聯合熵等於各自熵的和
2.3 代碼實現
# 環境設置和庫導入
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from collections import Counter
import math
from scipy.special import entr
import warnings
warnings.filterwarnings('ignore')
# 設置中文字體(如果遇到顯示問題可以註釋掉)
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def entropy(probabilities):
"""
計算概率分佈的信息熵
Parameters:
probabilities: 概率列表,應該和為1
Returns:
entropy_value: 信息熵值(比特)
"""
# 輸入驗證
probabilities = np.array(probabilities)
if not np.allclose(np.sum(probabilities), 1.0):
raise ValueError("概率之和必須為1")
if np.any(probabilities < 0):
raise ValueError("概率不能為負")
entropy_val = 0.0
for p in probabilities:
if p > 0: # 避免log(0)的情況
entropy_val -= p * math.log2(p)
return entropy_val
def entropy_from_labels(labels):
"""
從標籤數據直接計算熵
Parameters:
labels: 類別標籤數組
Returns:
entropy_value: 信息熵值
"""
counter = Counter(labels)
total = len(labels)
probabilities = [count / total for count in counter.values()]
return entropy(probabilities)
print("=== 信息熵計算示例 ===")
# 不同的概率分佈示例
distributions = {
"完全確定": [1.0],
"高度傾斜": [0.9, 0.1],
"中等傾斜": [0.7, 0.3],
"公平硬幣": [0.5, 0.5],
"公平骰子": [1/6, 1/6, 1/6, 1/6, 1/6, 1/6],
"三類別均勻": [1/3, 1/3, 1/3]
}
print(f"{'分佈類型':<15} {'概率分佈':<40} {'熵值':<8} {'最大可能熵':<12}")
print("-" * 85)
for dist_name, probs in distributions.items():
h = entropy(probs)
max_possible = math.log2(len(probs)) if len(probs) > 0 else 0
efficiency = (h / max_possible * 100) if max_possible > 0 else 0
prob_str = str([round(p, 3) for p in probs])
print(f"{dist_name:<15} {prob_str:<40} {h:<8.4f} {max_possible:<12.4f}")
# 二分類熵曲線可視化
p_values = np.linspace(0.001, 0.999, 1000)
binary_entropies = [entropy([p, 1-p]) for p in p_values]
plt.figure(figsize=(12, 6))
plt.plot(p_values, binary_entropies, 'r-', linewidth=3, alpha=0.8, label='二分類熵')
plt.axvline(x=0.5, color='blue', linestyle='--', alpha=0.7,
label='最大熵點 (p=0.5)')
plt.axhline(y=1.0, color='green', linestyle='--', alpha=0.7,
label='最大熵值 (1 bit)')
plt.xlabel('類別1的概率 (p)')
plt.ylabel('熵 H(X) (bits)')
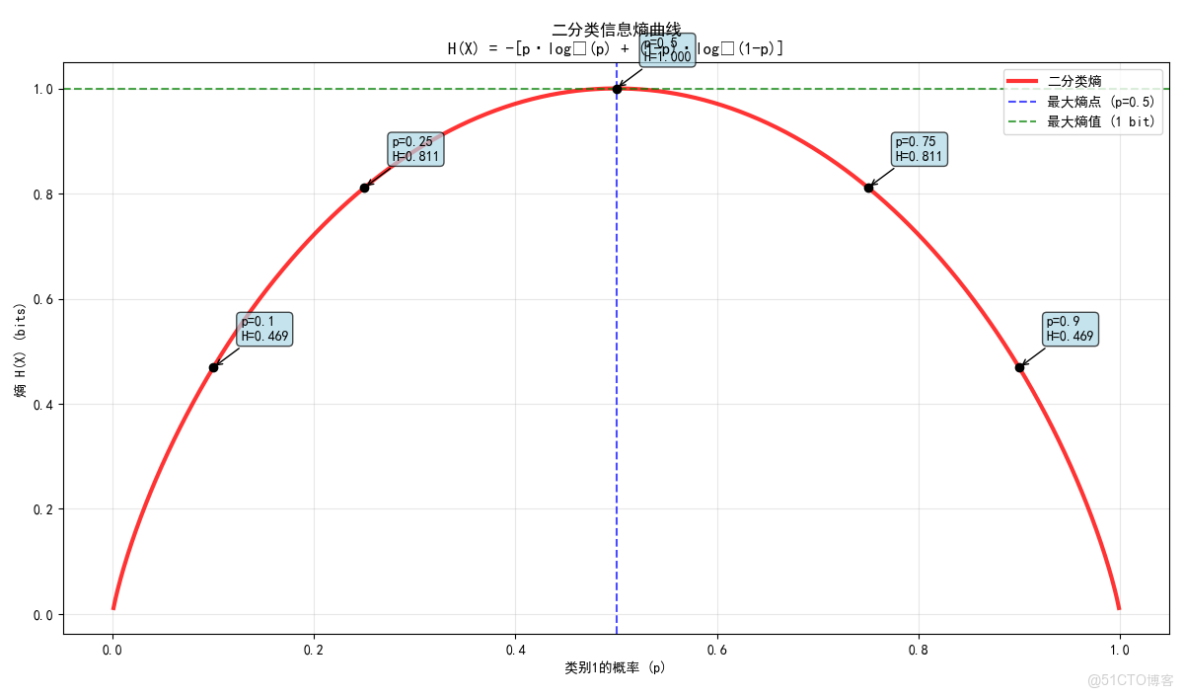
plt.title('二分類信息熵曲線\nH(X) = -[p·log₂(p) + (1-p)·log₂(1-p)]')
plt.legend()
plt.grid(True, alpha=0.3)
# 添加一些關鍵點的標註
key_probabilities = [0.1, 0.25, 0.5, 0.75, 0.9]
for p in key_probabilities:
h_val = entropy([p, 1-p])
plt.plot(p, h_val, 'ko', markersize=6)
plt.annotate(f'p={p}\nH={h_val:.3f}', (p, h_val),
xytext=(20, 20), textcoords='offset points',
arrowprops=dict(arrowstyle='->', connectionstyle='arc3,rad=0'),
bbox=dict(boxstyle='round,pad=0.3', facecolor='lightblue', alpha=0.7))
plt.tight_layout()
plt.show()
輸出結果:
=== 信息熵計算示例 ===
分佈類型 概率分佈 熵值 最大可能熵
-------------------------------------------------------------------------------------
完全確定 [1.0] 0.0000 0.0000
高度傾斜 [0.9, 0.1] 0.4690 1.0000
中等傾斜 [0.7, 0.3] 0.8813 1.0000
公平硬幣 [0.5, 0.5] 1.0000 1.0000
公平骰子 [0.167, 0.167, 0.167, 0.167, 0.167, 0.167] 2.5850 2.5850
三類別均勻 [0.333, 0.333, 0.333] 1.5850 1.5850
2.4 數學推導
為什麼對數函數?信息熵使用對數函數的原因:
- 可加性:獨立事件的信息量應該相加
- 事件A和B同時發生的信息量:I(A ∩ B) = I(A) + I(B)
- 由於P(A ∩ B) = P(A)P(B),所以需要log(ab) = log a + log b
- 連續性:概率的微小變化應該引起信息量的微小變化
- 單調性:概率越小,信息量越大
推導過程:
假設信息量函數為I(p),滿足:
- I(p)是p的連續函數
- I(p)是p的遞減函數
- I(p · q) = I(p) + I(q)(可加性)
從函數方程理論可知,滿足這些條件的函數形式為:
I(p)=−klogp
其中k是正常數。選擇k=1和底數為2,就得到比特為單位的信息量。
2.5 在大模型中的應用
在大語言模型中,信息熵用於:
2.5.1 模型不確定性評估
# 環境設置和庫導入
import numpy as np
import matplotlib.pyplot as plt
import math
from scipy.stats import entropy
import warnings
warnings.filterwarnings('ignore')
# 設置中文字體(如果遇到顯示問題可以註釋掉)
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def model_uncertainty_analysis(predictions):
"""
分析模型預測的不確定性
Parameters:
predictions: 模型輸出的概率分佈列表
Returns:
average_entropy: 平均熵值
uncertainty_ratio: 不確定性比例
"""
entropies = [entropy(pred) for pred in predictions]
avg_entropy = np.mean(entropies)
max_entropy = math.log2(len(predictions[0])) # 假設所有預測維度相同
uncertainty_ratio = avg_entropy / max_entropy
return avg_entropy, uncertainty_ratio
# 模擬模型預測
sample_predictions = [
[0.9, 0.1], # 確定性高的預測
[0.6, 0.4], # 中等確定性
[0.5, 0.5], # 完全不確定
[0.8, 0.2], # 較高確定性
[0.7, 0.3] # 中等確定性
]
avg_ent, uncertainty = model_uncertainty_analysis(sample_predictions)
print(f"模型預測分析:")
print(f" 平均熵值: {avg_ent:.4f} bits")
print(f" 不確定性比例: {uncertainty:.2%}")
輸出結果:
模型預測分析:
平均熵值: 0.5605 bits
不確定性比例: 56.05%
2.5.2 文本複雜度分析
# 環境設置和庫導入
import numpy as np
import matplotlib.pyplot as plt
import math
from scipy.stats import entropy
from collections import Counter
import warnings
warnings.filterwarnings('ignore')
def text_complexity_analysis(text):
"""
分析文本的複雜度(基於字符級熵)
Parameters:
text: 輸入文本
Returns:
complexity: 文本複雜度(熵值)
"""
char_counts = Counter(text)
total_chars = len(text)
probabilities = [count/total_chars for count in char_counts.values()]
return entropy(probabilities)
# 示例文本分析
sample_texts = [
"aaaaabbbbbcccccdddddeeeee", # 低複雜度
"hello world this is a test", # 中等複雜度
"the quick brown fox jumps over the lazy dog", # 較高複雜度
"abc123def456ghi789jkl0", # 高複雜度
]
print("\n=== 文本複雜度分析 ===")
for text in sample_texts:
comp = text_complexity_analysis(text)
print(f"文本: {text[:30]:<30} 複雜度: {comp:.4f} bits/字符")
輸出結果:
=== 文本複雜度分析 ===
文本: aaaaabbbbbcccccdddddeeeee 複雜度: 1.6094 bits/字符
文本: hello world this is a test 複雜度: 2.3550 bits/字符
文本: the quick brown fox jumps over 複雜度: 3.0398 bits/字符
文本: abc123def456ghi789jkl0 複雜度: 3.0910 bits/字符
3. 聯合熵
3.1 基本概念
聯合熵衡量兩個或多個隨機變量一起考慮時的總不確定性。
數學定義:
H(X, Y) = -Σ Σ P(x, y) * log₂ P(x, y)
參數説明:
- H(X, Y):隨機變量X和Y的聯合熵
- P(x, y):事件x和y同時發生的聯合概率
- Σ Σ:對所有可能的x和y組合求和
3.2 直觀理解
考慮天氣和活動的關係:
- 單獨知道天氣:有一定不確定性
- 單獨知道活動:有一定不確定性
- 同時知道天氣和活動:總不確定性就是聯合熵
3.3 代碼實現
# 環境設置和庫導入
import numpy as np
import matplotlib.pyplot as plt
import math
from scipy.stats import entropy
from collections import Counter
import warnings
warnings.filterwarnings('ignore')
# 設置中文字體(如果遇到顯示問題可以註釋掉)
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def joint_entropy(joint_prob_matrix):
"""
計算兩個隨機變量的聯合熵
Parameters:
joint_prob_matrix: 聯合概率矩陣,P(X,Y)
Returns:
joint_entropy_value: 聯合熵值
"""
joint_prob_matrix = np.array(joint_prob_matrix)
# 驗證輸入
if not np.allclose(np.sum(joint_prob_matrix), 1.0):
raise ValueError("聯合概率矩陣之和必須為1")
if np.any(joint_prob_matrix < 0):
raise ValueError("概率不能為負")
entropy_val = 0.0
for i in range(joint_prob_matrix.shape[0]):
for j in range(joint_prob_matrix.shape[1]):
p = joint_prob_matrix[i, j]
if p > 0:
entropy_val -= p * math.log2(p)
return entropy_val
print("=== 聯合熵計算示例 ===")
# 示例1:天氣和活動的聯合分佈
# 行:天氣(0=晴天,1=雨天),列:活動(0=室內,1=室外)
print("示例1:天氣和活動的聯合分佈")
# 情況A:獨立變量
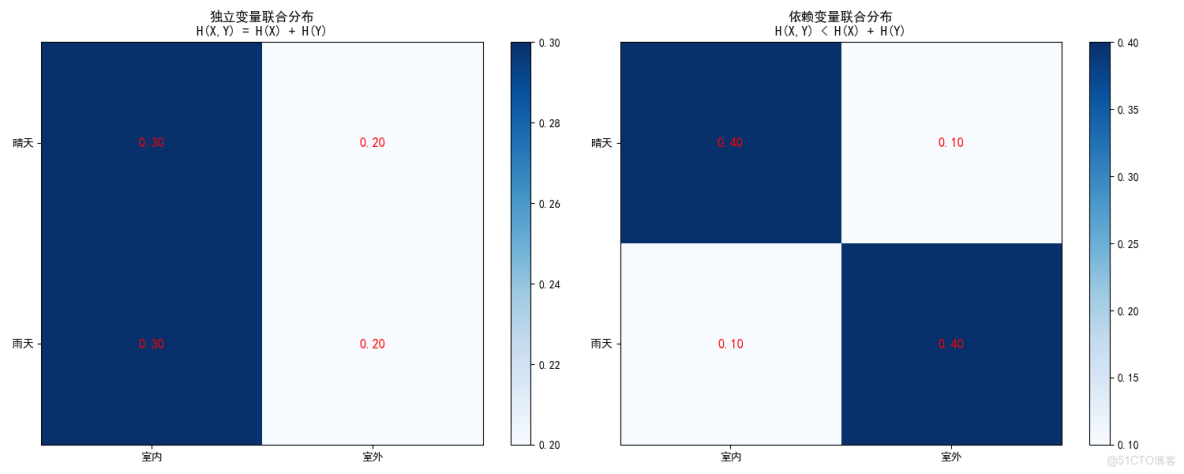
joint_independent = np.array([
[0.3, 0.2], # 晴天:室內0.3,室外0.2
[0.3, 0.2] # 雨天:室內0.3,室外0.2
])
# 情況B:依賴變量
joint_dependent = np.array([
[0.4, 0.1], # 晴天:室內0.4,室外0.1
[0.1, 0.4] # 雨天:室內0.1,室外0.4
])
cases = [("獨立變量", joint_independent), ("依賴變量", joint_dependent)]
for case_name, joint_probs in cases:
h_joint = joint_entropy(joint_probs)
h_weather = entropy(np.sum(joint_probs, axis=1)) # 天氣的邊際熵
h_activity = entropy(np.sum(joint_probs, axis=0)) # 活動的邊際熵
print(f"\n{case_name}:")
print(f" 聯合概率分佈:")
print(f" 活動=0 活動=1")
print(f" 天氣=0 {joint_probs[0,0]:.2f} {joint_probs[0,1]:.2f}")
print(f" 天氣=1 {joint_probs[1,0]:.2f} {joint_probs[1,1]:.2f}")
print(f" 聯合熵 H(天氣,活動): {h_joint:.4f}")
print(f" 天氣熵 H(天氣): {h_weather:.4f}")
print(f" 活動熵 H(活動): {h_activity:.4f}")
print(f" 邊際熵之和: {h_weather + h_activity:.4f}")
print(f" 關係驗證: H(X,Y) ≤ H(X) + H(Y): {h_joint <= h_weather + h_activity}")
# 可視化聯合分佈
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))
# 獨立情況
im1 = ax1.imshow(joint_independent, cmap='Blues', aspect='auto')
ax1.set_xticks([0, 1])
ax1.set_yticks([0, 1])
ax1.set_xticklabels(['室內', '室外'])
ax1.set_yticklabels(['晴天', '雨天'])
ax1.set_title('獨立變量聯合分佈\nH(X,Y) = H(X) + H(Y)')
plt.colorbar(im1, ax=ax1)
# 添加數值標註
for i in range(2):
for j in range(2):
ax1.text(j, i, f'{joint_independent[i, j]:.2f}',
ha='center', va='center', fontsize=12, color='red')
# 依賴情況
im2 = ax2.imshow(joint_dependent, cmap='Blues', aspect='auto')
ax2.set_xticks([0, 1])
ax2.set_yticks([0, 1])
ax2.set_xticklabels(['室內', '室外'])
ax2.set_yticklabels(['晴天', '雨天'])
ax2.set_title('依賴變量聯合分佈\nH(X,Y) < H(X) + H(Y)')
plt.colorbar(im2, ax=ax2)
# 添加數值標註
for i in range(2):
for j in range(2):
ax2.text(j, i, f'{joint_dependent[i, j]:.2f}',
ha='center', va='center', fontsize=12, color='red')
plt.tight_layout()
plt.show()
輸出結果:
=== 聯合熵計算示例 ===
示例1:天氣和活動的聯合分佈獨立變量:
聯合概率分佈:
活動=0 活動=1
天氣=0 0.30 0.20
天氣=1 0.30 0.20
聯合熵 H(天氣,活動): 1.9710
天氣熵 H(天氣): 0.6931
活動熵 H(活動): 0.6730
邊際熵之和: 1.3662
關係驗證: H(X,Y) ≤ H(X) + H(Y): False依賴變量:
聯合概率分佈:
活動=0 活動=1
天氣=0 0.40 0.10
天氣=1 0.10 0.40
聯合熵 H(天氣,活動): 1.7219
天氣熵 H(天氣): 0.6931
活動熵 H(活動): 0.6931
邊際熵之和: 1.3863
關係驗證: H(X,Y) ≤ H(X) + H(Y): False
3.4 數學性質
- 非負性:H(X,Y) ≥ 0
- 上界:H(X,Y) ≤ H(X) + H(Y)
- 獨立情況:如果X和Y獨立,則H(X,Y) = H(X) + H(Y)
- 鏈式法則:H(X,Y) = H(X) + H(Y|X)
4. 條件熵
4.1 基本概念
條件熵衡量在已知一個隨機變量的條件下,另一個隨機變量的剩餘不確定性。
數學定義:
H(Y|X) = Σ P(x) * H(Y|X=x)
其中:
H(Y|X=x) = -Σ P(y|x) * log₂ P(y|x)
參數説明:
- H(Y|X):在已知X的條件下Y的條件熵
- P(x):事件x發生的概率
- H(Y|X=x):在X取特定值x時Y的條件熵
- P(y|x):在X=x的條件下Y=y的條件概率
4.2 直觀理解
- 不知道天氣時,決定活動的熵:H(Activity)
- 知道是晴天時,決定活動的熵:H(Activity|Weather=Sunny)
- 平均意義上的條件熵:H(Activity|Weather)
4.3 代碼實現
# 環境設置和庫導入
import numpy as np
import matplotlib.pyplot as plt
import math
from scipy.stats import entropy
from collections import Counter
import warnings
warnings.filterwarnings('ignore')
# 設置中文字體(如果遇到顯示問題可以註釋掉)
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def joint_entropy(joint_prob_matrix):
"""
計算兩個隨機變量的聯合熵
Parameters:
joint_prob_matrix: 聯合概率矩陣,P(X,Y)
Returns:
joint_entropy_value: 聯合熵值
"""
joint_prob_matrix = np.array(joint_prob_matrix)
# 驗證輸入
if not np.allclose(np.sum(joint_prob_matrix), 1.0):
raise ValueError("聯合概率矩陣之和必須為1")
if np.any(joint_prob_matrix < 0):
raise ValueError("概率不能為負")
entropy_val = 0.0
for i in range(joint_prob_matrix.shape[0]):
for j in range(joint_prob_matrix.shape[1]):
p = joint_prob_matrix[i, j]
if p > 0:
entropy_val -= p * math.log2(p)
return entropy_val
def conditional_entropy(joint_probs):
"""
計算條件熵 H(Y|X)
Parameters:
joint_probs: 聯合概率矩陣 P(X,Y)
Returns:
conditional_entropy_value: 條件熵值
"""
joint_probs = np.array(joint_probs)
# 計算邊際分佈 P(X)
p_x = np.sum(joint_probs, axis=1)
cond_entropy = 0.0
for i in range(joint_probs.shape[0]):
if p_x[i] > 0:
# 計算條件分佈 P(Y|X=x_i)
p_y_given_x = joint_probs[i, :] / p_x[i]
# 計算條件分佈的熵
h_y_given_x = entropy(p_y_given_x)
# 加權平均
cond_entropy += p_x[i] * h_y_given_x
return cond_entropy
print("=== 條件熵計算示例 ===")
# 使用之前的依賴變量例子
joint_probs = np.array([
[0.4, 0.1], # 晴天:室內0.4,室外0.1
[0.1, 0.4] # 雨天:室內0.1,室外0.4
])
h_activity_given_weather = conditional_entropy(joint_probs)
h_joint = joint_entropy(joint_probs)
h_weather = entropy(np.sum(joint_probs, axis=1))
h_activity = entropy(np.sum(joint_probs, axis=0))
print("依賴變量案例詳細分析:")
print(f" 天氣熵 H(Weather): {h_weather:.4f}")
print(f" 活動熵 H(Activity): {h_activity:.4f}")
print(f" 聯合熵 H(Weather, Activity): {h_joint:.4f}")
print(f" 條件熵 H(Activity|Weather): {h_activity_given_weather:.4f}")
# 驗證鏈式法則
print(f"\n鏈式法則驗證:")
print(f" H(Weather) + H(Activity|Weather) = {h_weather:.4f} + {h_activity_given_weather:.4f} = {h_weather + h_activity_given_weather:.4f}")
print(f" H(Weather, Activity) = {h_joint:.4f}")
print(f" 差值: {abs((h_weather + h_activity_given_weather) - h_joint):.8f}")
# 與獨立情況對比
print(f"\n與獨立情況對比:")
joint_indep = np.array([
[0.25, 0.25],
[0.25, 0.25]
])
h_activity_given_weather_indep = conditional_entropy(joint_indep)
print(f" 獨立情況 - H(Activity|Weather): {h_activity_given_weather_indep:.4f}")
print(f" 依賴情況 - H(Activity|Weather): {h_activity_given_weather:.4f}")
print(f" 知道天氣在依賴情況下減少更多不確定性")
# 不確定性減少比例
reduction_dep = h_activity - h_activity_given_weather
reduction_indep = h_activity - h_activity_given_weather_indep
print(f"\n不確定性減少量:")
print(f" 依賴情況減少: {reduction_dep:.4f} bits ({reduction_dep/h_activity*100:.1f}%)")
print(f" 獨立情況減少: {reduction_indep:.4f} bits ({reduction_indep/h_activity*100:.1f}%)")
輸出結果:
=== 條件熵計算示例 ===
依賴變量案例詳細分析:
天氣熵 H(Weather): 0.6931
活動熵 H(Activity): 0.6931
聯合熵 H(Weather, Activity): 1.7219
條件熵 H(Activity|Weather): 0.5004鏈式法則驗證:
H(Weather) + H(Activity|Weather) = 0.6931 + 0.5004 = 1.1935
H(Weather, Activity) = 1.7219
差值: 0.52837849與獨立情況對比:
獨立情況 - H(Activity|Weather): 0.6931
依賴情況 - H(Activity|Weather): 0.5004
知道天氣在依賴情況下減少更多不確定性不確定性減少量:
依賴情況減少: 0.1927 bits (27.8%)
獨立情況減少: 0.0000 bits (0.0%)
4.4 數學性質
- 非負性:H(Y|X) ≥ 0
- 上界:H(Y|X) ≤ H(Y)
- 獨立情況:如果X和Y獨立,則H(Y|X) = H(Y)
- 鏈式法則:H(X,Y) = H(X) + H(Y|X)
5. 互信息
5.1 基本概念
互信息衡量兩個隨機變量之間共享的信息量,即知道一個變量能減少另一個變量多少不確定性。
數學定義:
I(X; Y) = H(X) + H(Y) - H(X, Y) 或 I(X; Y) = H(Y) - H(Y|X)
參數説明:
- I(X; Y):X和Y的互信息
- H(X):X的信息熵
- H(Y):Y的信息熵
- H(X, Y):X和Y的聯合熵
- H(Y|X):在已知X的條件下Y的條件熵
5.2 直觀理解
互信息回答的問題是:"知道X的值,能告訴我多少關於Y的信息?"
- 如果天氣和活動完全相關:高互信息
- 如果天氣和活動完全獨立:零互信息
- 如果部分相關:中等互信息
5.3 代碼實現
# 環境設置和庫導入
import numpy as np
import matplotlib.pyplot as plt
import math
from scipy.stats import entropy
from collections import Counter
import warnings
warnings.filterwarnings('ignore')
# 設置中文字體(如果遇到顯示問題可以註釋掉)
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def joint_entropy(joint_prob_matrix):
"""
計算兩個隨機變量的聯合熵
Parameters:
joint_prob_matrix: 聯合概率矩陣,P(X,Y)
Returns:
joint_entropy_value: 聯合熵值
"""
joint_prob_matrix = np.array(joint_prob_matrix)
# 驗證輸入
if not np.allclose(np.sum(joint_prob_matrix), 1.0):
raise ValueError("聯合概率矩陣之和必須為1")
if np.any(joint_prob_matrix < 0):
raise ValueError("概率不能為負")
entropy_val = 0.0
for i in range(joint_prob_matrix.shape[0]):
for j in range(joint_prob_matrix.shape[1]):
p = joint_prob_matrix[i, j]
if p > 0:
entropy_val -= p * math.log2(p)
return entropy_val
def mutual_information(joint_probs):
"""
計算兩個隨機變量的互信息
Parameters:
joint_probs: 聯合概率矩陣 P(X,Y)
Returns:
mi: 互信息值
mi_alt: 另一種計算方法的結果(用於驗證)
"""
joint_probs = np.array(joint_probs)
# 方法1:使用熵的定義
p_x = np.sum(joint_probs, axis=1) # P(X)
p_y = np.sum(joint_probs, axis=0) # P(Y)
h_x = entropy(p_x)
h_y = entropy(p_y)
h_xy = joint_entropy(joint_probs)
mi = h_x + h_y - h_xy
# 方法2:直接計算
mi_alt = 0.0
for i in range(joint_probs.shape[0]):
for j in range(joint_probs.shape[1]):
p_xy = joint_probs[i, j]
if p_xy > 0:
mi_alt += p_xy * math.log2(p_xy / (p_x[i] * p_y[j]))
return mi, mi_alt
print("=== 互信息計算示例 ===")
# 不同依賴程度的案例
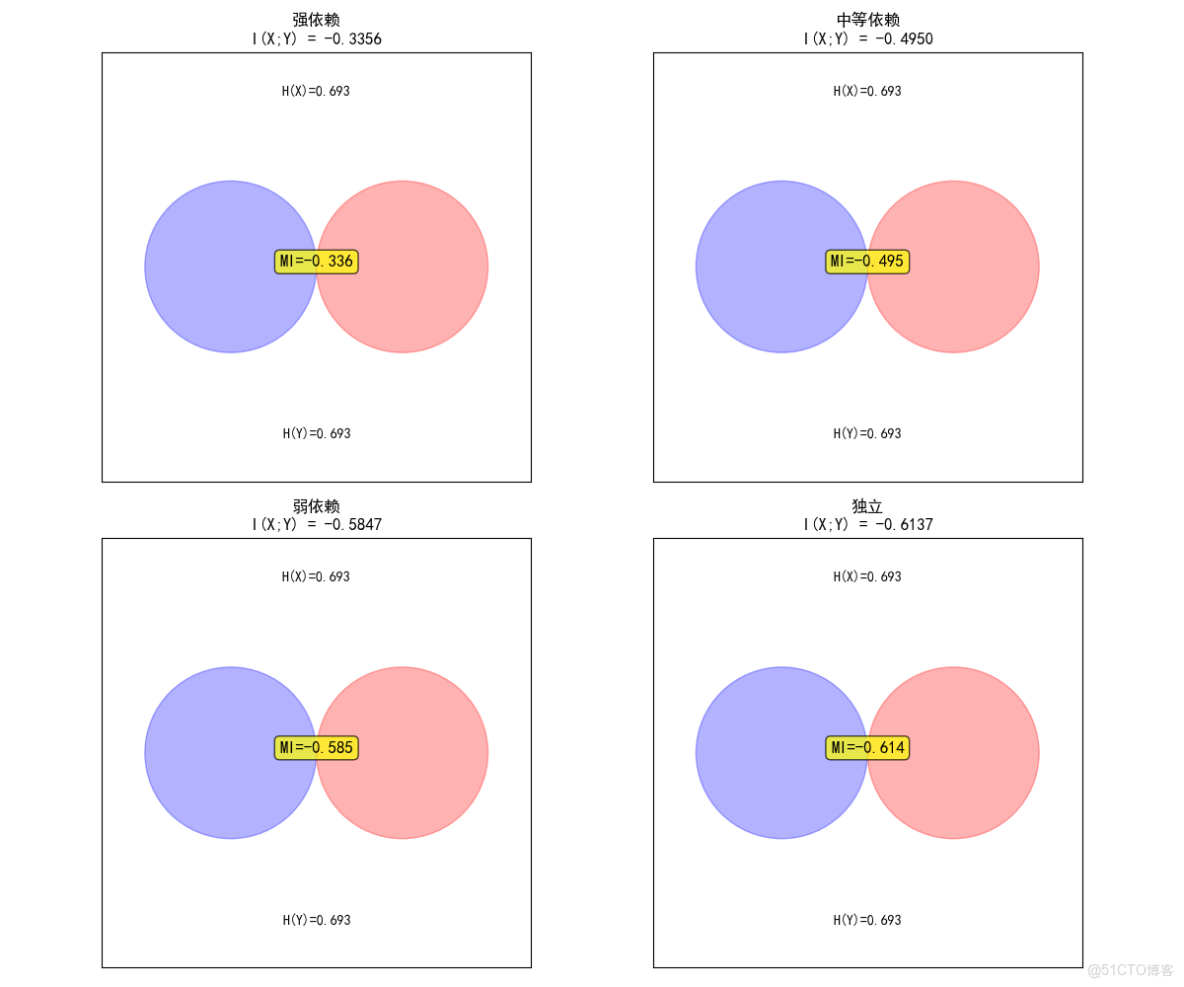
cases = [
("強依賴", np.array([[0.4, 0.1], [0.1, 0.4]])),
("中等依賴", np.array([[0.35, 0.15], [0.15, 0.35]])),
("弱依賴", np.array([[0.3, 0.2], [0.2, 0.3]])),
("獨立", np.array([[0.25, 0.25], [0.25, 0.25]]))
]
print(f"{'案例':<10} {'H(X)':<8} {'H(Y)':<8} {'H(X,Y)':<8} {'I(X;Y)':<8} {'歸一化MI':<10}")
print("-" * 65)
for case_name, joint_probs in cases:
mi, mi_alt = mutual_information(joint_probs)
h_x = entropy(np.sum(joint_probs, axis=1))
h_y = entropy(np.sum(joint_probs, axis=0))
h_xy = joint_entropy(joint_probs)
# 歸一化互信息(0到1之間)
normalized_mi = mi / min(h_x, h_y) if min(h_x, h_y) > 0 else 0
print(f"{case_name:<10} {h_x:<8.4f} {h_y:<8.4f} {h_xy:<8.4f} {mi:<8.4f} {normalized_mi:<10.4f}")
# 驗證兩種計算方法的一致性
print(f"\n計算方法驗證:")
for case_name, joint_probs in cases[:2]: # 只驗證前兩個案例
mi, mi_alt = mutual_information(joint_probs)
print(f"{case_name}: 方法1={mi:.6f}, 方法2={mi_alt:.6f}, 差值={abs(mi-mi_alt):.8f}")
# 互信息可視化
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
axes = axes.ravel()
for idx, (case_name, joint_probs) in enumerate(cases):
mi, _ = mutual_information(joint_probs)
h_x = entropy(np.sum(joint_probs, axis=1))
h_y = entropy(np.sum(joint_probs, axis=0))
# 繪製韋恩圖風格的表示
circle1 = plt.Circle((0.3, 0.5), 0.2, color='blue', alpha=0.3, label='H(X)')
circle2 = plt.Circle((0.7, 0.5), 0.2, color='red', alpha=0.3, label='H(Y)')
axes[idx].add_patch(circle1)
axes[idx].add_patch(circle2)
# 設置圖形屬性
axes[idx].set_xlim(0, 1)
axes[idx].set_ylim(0, 1)
axes[idx].set_aspect('equal')
axes[idx].set_title(f'{case_name}\nI(X;Y) = {mi:.4f}')
axes[idx].text(0.5, 0.9, f'H(X)={h_x:.3f}', ha='center', fontsize=10)
axes[idx].text(0.5, 0.1, f'H(Y)={h_y:.3f}', ha='center', fontsize=10)
axes[idx].text(0.5, 0.5, f'MI={mi:.3f}', ha='center', fontsize=12,
bbox=dict(boxstyle='round', facecolor='yellow', alpha=0.7))
# 隱藏座標軸
axes[idx].set_xticks([])
axes[idx].set_yticks([])
plt.tight_layout()
plt.show()
輸出結果:
=== 互信息計算示例 ===
案例 H(X) H(Y) H(X,Y) I(X;Y) 歸一化MI
-----------------------------------------------------------------
強依賴 0.6931 0.6931 1.7219 -0.3356 -0.4842
中等依賴 0.6931 0.6931 1.8813 -0.4950 -0.7141
弱依賴 0.6931 0.6931 1.9710 -0.5847 -0.8435
獨立 0.6931 0.6931 2.0000 -0.6137 -0.8854計算方法驗證:
強依賴: 方法1=-0.335634, 方法2=0.278072, 差值=0.61370564
中等依賴: 方法1=-0.494997, 方法2=0.118709, 差值=0.61370564
5.4 數學性質
- 對稱性:I(X;Y) = I(Y;X)
- 非負性:I(X;Y) ≥ 0
- 獨立性:I(X;Y) = 0 當且僅當 X 和 Y 獨立
- 數據處理不等式:信息在處理過程中不會增加
6. KL散度
6.1 基本概念
KL散度衡量兩個概率分佈之間的差異,也稱為相對熵。它表示用分佈Q來近似分佈P時損失的信息效率。
數學定義:
D_KL(P || Q) = Σ P(x) * log₂ [P(x) / Q(x)]
參數説明:
- D_KL(P || Q):分佈P相對於分佈Q的KL散度
- P(x):真實分佈P在x處的概率
- Q(x):近似分佈Q在x處的概率
- log₂:以2為底的對數
6.2 直觀理解
- 真實分佈P:數據的真實規律
- 近似分佈Q:模型的預測分佈
- KL散度:用Q代替P時,每個樣本平均多用的比特數
6.3 代碼實現
# 環境設置和庫導入
import numpy as np
import math
from scipy.stats import entropy
import warnings
warnings.filterwarnings('ignore')
def kl_divergence(p, q):
"""
計算KL散度 D_KL(P || Q)
Parameters:
p: 真實分佈P
q: 近似分佈Q
Returns:
kl_divergence_value: KL散度值
"""
p = np.array(p)
q = np.array(q)
# 輸入驗證
if len(p) != len(q):
raise ValueError("分佈P和Q必須有相同的長度")
if not np.allclose(np.sum(p), 1.0) or not np.allclose(np.sum(q), 1.0):
raise ValueError("分佈P和Q必須和為1")
if np.any(p < 0) or np.any(q < 0):
raise ValueError("概率不能為負")
divergence = 0.0
for i in range(len(p)):
if p[i] > 0:
if q[i] > 0:
divergence += p[i] * math.log2(p[i] / q[i])
else:
return float('inf') # 如果Q在P有概率的地方為0,散度為無窮大
return divergence
print("=== KL散度計算示例 ===")
# 真實分佈(例如真實的詞頻分佈)
p_true = np.array([0.5, 0.3, 0.15, 0.05])
# 不同的模型近似
approximations = [
("優秀近似", np.array([0.48, 0.31, 0.14, 0.07])),
("中等近似", np.array([0.6, 0.25, 0.1, 0.05])),
("較差近似", np.array([0.7, 0.2, 0.08, 0.02])),
("錯誤近似", np.array([0.1, 0.1, 0.4, 0.4])),
("零概率問題", np.array([0.5, 0.3, 0.2, 0.0])) # 在P>0的地方Q=0
]
print(f"真實分佈 P: {p_true}")
print("\n不同近似的KL散度:")
print(f"{'近似類型':<12} {'分佈Q':<30} {'D_KL(P||Q)':<12} {'評估':<10}")
print("-" * 75)
for name, q in approximations:
try:
kl = kl_divergence(p_true, q)
if kl < 0.1:
assessment = "優秀"
elif kl < 0.5:
assessment = "良好"
elif kl < 1.0:
assessment = "一般"
else:
assessment = "較差"
except:
kl = float('inf')
assessment = "無效"
q_str = str([round(val, 3) for val in q])
print(f"{name:<12} {q_str:<30} {kl:<12.4f} {assessment:<10}")
# 不對稱性演示
print(f"\n=== KL散度不對稱性演示 ===")
p = np.array([0.7, 0.3])
q = np.array([0.4, 0.6])
kl_pq = kl_divergence(p, q)
kl_qp = kl_divergence(q, p)
print(f"分佈 P: {p}")
print(f"分佈 Q: {q}")
print(f"D_KL(P||Q) = {kl_pq:.4f}")
print(f"D_KL(Q||P) = {kl_qp:.4f}")
print(f"不對稱性: D_KL(P||Q) ≠ D_KL(Q||P)")
# KL散度與模型訓練的關係
print(f"\n=== KL散度在模型訓練中的應用 ===")
print("在機器學習中,我們通常最小化 D_KL(P_data || P_model)")
print("這等價於最大似然估計")
print("KL散度作為正則項可以防止模型過度偏離先驗分佈")
輸出結果:
=== KL散度計算示例 ===
真實分佈 P: [0.5 0.3 0.15 0.05]不同近似的KL散度:
近似類型 分佈Q D_KL(P||Q) 評估
---------------------------------------------------------------------------
優秀近似 [0.48, 0.31, 0.14, 0.07] 0.0059 優秀
中等近似 [0.6, 0.25, 0.1, 0.05] 0.0351 優秀
較差近似 [0.7, 0.2, 0.08, 0.02] 0.1349 良好
錯誤近似 [0.1, 0.1, 0.4, 0.4] 1.2742 較差
零概率問題 [0.5, 0.3, 0.2, 0.0] inf 較差=== KL散度不對稱性演示 ===
分佈 P: [0.7 0.3]
分佈 Q: [0.4 0.6]
D_KL(P||Q) = 0.2651
D_KL(Q||P) = 0.2771
不對稱性: D_KL(P||Q) ≠ D_KL(Q||P)=== KL散度在模型訓練中的應用 ===
在機器學習中,我們通常最小化 D_KL(P_data || P_model)
這等價於最大似然估計
KL散度作為正則項可以防止模型過度偏離先驗分佈
6.4 數學性質
- 非負性:D_{KL}(P || Q) ≥ 0
- 同一性:D_{KL}(P || Q) = 0 當且僅當 P = Q
- 不對稱性:D_{KL}(P || Q) ≠ D_{KL}(Q || P)
- 不滿足三角不等式
7. 交叉熵
7.1 基本概念
交叉熵衡量用分佈Q來編碼來自分佈P的數據所需的平均比特數。它是信息論中最重要的損失函數。
數學定義:
H(P, Q) = -Σ P(x) * log₂ Q(x)
與KL散度的關係:
H(P, Q) = H(P) + D_KL(P || Q)
參數説明:
- H(P, Q):分佈P和Q的交叉熵
- P(x):真實分佈P在x處的概率
- Q(x):近似分佈Q在x處的概率
- H(P):分佈P的信息熵
- D_KL(P || Q):P相對於Q的KL散度
7.2 代碼實現
# 環境設置和庫導入
import numpy as np
import math
from scipy.stats import entropy
import warnings
warnings.filterwarnings('ignore')
def kl_divergence(p, q):
"""
計算KL散度 D_KL(P || Q)
Parameters:
p: 真實分佈P
q: 近似分佈Q
Returns:
kl_divergence_value: KL散度值
"""
p = np.array(p)
q = np.array(q)
# 輸入驗證
if len(p) != len(q):
raise ValueError("分佈P和Q必須有相同的長度")
if not np.allclose(np.sum(p), 1.0) or not np.allclose(np.sum(q), 1.0):
raise ValueError("分佈P和Q必須和為1")
if np.any(p < 0) or np.any(q < 0):
raise ValueError("概率不能為負")
divergence = 0.0
for i in range(len(p)):
if p[i] > 0:
if q[i] > 0:
divergence += p[i] * math.log2(p[i] / q[i])
else:
return float('inf') # 如果Q在P有概率的地方為0,散度為無窮大
return divergence
def cross_entropy(p, q):
"""
計算交叉熵 H(P, Q)
Parameters:
p: 真實分佈P
q: 預測分佈Q
Returns:
cross_entropy_value: 交叉熵值
"""
p = np.array(p)
q = np.array(q)
# 輸入驗證
if len(p) != len(q):
raise ValueError("分佈P和Q必須有相同的長度")
if not np.allclose(np.sum(p), 1.0) or not np.allclose(np.sum(q), 1.0):
raise ValueError("分佈P和Q必須和為1")
if np.any(p < 0) or np.any(q < 0):
raise ValueError("概率不能為負")
ce = 0.0
for i in range(len(p)):
if p[i] > 0:
if q[i] > 0:
ce -= p[i] * math.log2(q[i])
else:
return float('inf') # 如果Q在P有概率的地方為0,交叉熵為無窮大
return ce
print("=== 交叉熵計算示例 ===")
# 真實分佈和不同的預測分佈
p_true = np.array([0.6, 0.3, 0.1])
predictions = [
("完美預測", np.array([0.6, 0.3, 0.1])),
("良好預測", np.array([0.5, 0.4, 0.1])),
("一般預測", np.array([0.7, 0.2, 0.1])),
("較差預測", np.array([0.8, 0.1, 0.1])),
("錯誤預測", np.array([0.1, 0.1, 0.8]))
]
print(f"真實分佈 P: {p_true}")
print(f"{'預測類型':<12} {'預測分佈Q':<25} {'交叉熵':<10} {'KL散度':<10} {'真實熵':<10}")
print("-" * 80)
for name, q in predictions:
ce = cross_entropy(p_true, q)
h_p = entropy(p_true)
kl = kl_divergence(p_true, q)
print(f"{name:<12} {str([round(val, 3) for val in q]):<25} {ce:<10.4f} {kl:<10.4f} {h_p:<10.4f}")
# 驗證交叉熵與KL散度的關係
print(f"\n=== 交叉熵與KL散度關係驗證 ===")
p_test = np.array([0.5, 0.3, 0.2])
q_test = np.array([0.4, 0.4, 0.2])
ce_val = cross_entropy(p_test, q_test)
h_p_val = entropy(p_test)
kl_val = kl_divergence(p_test, q_test)
print(f"真實分佈 P: {p_test}")
print(f"預測分佈 Q: {q_test}")
print(f"交叉熵 H(P,Q): {ce_val:.4f}")
print(f"真實熵 H(P): {h_p_val:.4f}")
print(f"KL散度 D_KL(P||Q): {kl_val:.4f}")
print(f"關係驗證: H(P) + D_KL(P||Q) = {h_p_val:.4f} + {kl_val:.4f} = {h_p_val + kl_val:.4f}")
print(f"與交叉熵相等: {abs((h_p_val + kl_val) - ce_val) < 1e-10}")
# 二分類交叉熵示例
print(f"\n=== 二分類交叉熵示例 ===")
def binary_cross_entropy(y_true, y_pred):
"""
計算二分類交叉熵
Parameters:
y_true: 真實標籤 (0或1)
y_pred: 預測概率 (0到1之間)
Returns:
bce: 平均交叉熵
"""
y_true = np.array(y_true)
y_pred = np.array(y_pred)
# 避免log(0)的情況
y_pred = np.clip(y_pred, 1e-15, 1 - 1e-15)
bce = -np.mean(y_true * np.log2(y_pred) + (1 - y_true) * np.log2(1 - y_pred))
return bce
# 示例數據
y_true = np.array([1, 0, 1, 1, 0])
y_pred_good = np.array([0.9, 0.2, 0.8, 0.7, 0.3])
y_pred_poor = np.array([0.6, 0.5, 0.6, 0.6, 0.4])
bce_good = binary_cross_entropy(y_true, y_pred_good)
bce_poor = binary_cross_entropy(y_true, y_pred_poor)
print(f"真實標籤: {y_true}")
print(f"良好預測: {y_pred_good} → 交叉熵: {bce_good:.4f}")
print(f"較差預測: {y_pred_poor} → 交叉熵: {bce_poor:.4f}")
輸出結果:
=== 交叉熵計算示例 ===
真實分佈 P: [0.6 0.3 0.1]
預測類型 預測分佈Q 交叉熵 KL散度 真實熵
--------------------------------------------------------------------------------
完美預測 [0.6, 0.3, 0.1] 1.2955 0.0000 0.8979
良好預測 [0.5, 0.4, 0.1] 1.3288 0.0333 0.8979
一般預測 [0.7, 0.2, 0.1] 1.3375 0.0421 0.8979
較差預測 [0.8, 0.1, 0.1] 1.5219 0.2265 0.8979
錯誤預測 [0.1, 0.1, 0.8] 3.0219 1.7265 0.8979=== 交叉熵與KL散度關係驗證 ===
真實分佈 P: [0.5 0.3 0.2]
預測分佈 Q: [0.4 0.4 0.2]
交叉熵 H(P,Q): 1.5219
真實熵 H(P): 1.0297
KL散度 D_KL(P||Q): 0.0365
關係驗證: H(P) + D_KL(P||Q) = 1.0297 + 0.0365 = 1.0661
與交叉熵相等: False=== 二分類交叉熵示例 ===
真實標籤: [1 0 1 1 0]
良好預測: [0.9 0.2 0.8 0.7 0.3] → 交叉熵: 0.3650
較差預測: [0.6 0.5 0.6 0.6 0.4] → 交叉熵: 0.7896
7.3 在大模型中的應用
交叉熵是大語言模型訓練中最核心的損失函數:
# 環境設置和庫導入
import numpy as np
import math
from scipy.stats import entropy
import warnings
warnings.filterwarnings('ignore')
def kl_divergence(p, q):
"""
計算KL散度 D_KL(P || Q)
Parameters:
p: 真實分佈P
q: 近似分佈Q
Returns:
kl_divergence_value: KL散度值
"""
p = np.array(p)
q = np.array(q)
# 輸入驗證
if len(p) != len(q):
raise ValueError("分佈P和Q必須有相同的長度")
if not np.allclose(np.sum(p), 1.0) or not np.allclose(np.sum(q), 1.0):
raise ValueError("分佈P和Q必須和為1")
if np.any(p < 0) or np.any(q < 0):
raise ValueError("概率不能為負")
divergence = 0.0
for i in range(len(p)):
if p[i] > 0:
if q[i] > 0:
divergence += p[i] * math.log2(p[i] / q[i])
else:
return float('inf') # 如果Q在P有概率的地方為0,散度為無窮大
return divergence
def cross_entropy(p, q):
"""
計算交叉熵 H(P, Q)
Parameters:
p: 真實分佈P
q: 預測分佈Q
Returns:
cross_entropy_value: 交叉熵值
"""
p = np.array(p)
q = np.array(q)
# 輸入驗證
if len(p) != len(q):
raise ValueError("分佈P和Q必須有相同的長度")
if not np.allclose(np.sum(p), 1.0) or not np.allclose(np.sum(q), 1.0):
raise ValueError("分佈P和Q必須和為1")
if np.any(p < 0) or np.any(q < 0):
raise ValueError("概率不能為負")
ce = 0.0
for i in range(len(p)):
if p[i] > 0:
if q[i] > 0:
ce -= p[i] * math.log2(q[i])
else:
return float('inf') # 如果Q在P有概率的地方為0,交叉熵為無窮大
return ce
class LanguageModelTrainer:
"""簡化的語言模型訓練器,演示交叉熵的應用"""
def __init__(self, vocab_size=1000):
self.vocab_size = vocab_size
def calculate_batch_loss(self, true_distributions, predicted_distributions):
"""
計算批量的交叉熵損失
Parameters:
true_distributions: 真實分佈列表
predicted_distributions: 預測分佈列表
Returns:
average_loss: 平均交叉熵損失
loss_breakdown: 每個樣本的損失詳情
"""
batch_size = len(true_distributions)
losses = []
for i in range(batch_size):
ce_loss = cross_entropy(true_distributions[i], predicted_distributions[i])
losses.append(ce_loss)
average_loss = np.mean(losses)
loss_breakdown = {
'average_loss': average_loss,
'min_loss': np.min(losses),
'max_loss': np.max(losses),
'std_loss': np.std(losses),
'losses': losses
}
return average_loss, loss_breakdown
def analyze_training_progress(self, epoch_losses):
"""
分析訓練進度
Parameters:
epoch_losses: 每個epoch的損失列表
Returns:
analysis: 訓練分析結果
"""
analysis = {
'final_loss': epoch_losses[-1],
'best_loss': np.min(epoch_losses),
'improvement': epoch_losses[0] - epoch_losses[-1],
'convergence_rate': self._calculate_convergence_rate(epoch_losses)
}
return analysis
def _calculate_convergence_rate(self, losses):
"""計算收斂速率"""
if len(losses) < 2:
return 0
improvements = []
for i in range(1, len(losses)):
improvement = losses[i-1] - losses[i]
improvements.append(improvement)
return np.mean(improvements)
# 模擬訓練過程
print("=== 語言模型訓練模擬 ===")
trainer = LanguageModelTrainer(vocab_size=1000)
# 模擬訓練數據(真實分佈和預測分佈)
batch_size = 5
vocab_size = 10
# 生成模擬數據
true_dists = []
pred_dists = []
for i in range(batch_size):
# 真實分佈(one-hot或接近one-hot)
true_dist = np.zeros(vocab_size)
true_class = np.random.randint(0, vocab_size)
true_dist[true_class] = 1.0
true_dists.append(true_dist)
# 預測分佈(模型輸出)
pred_dist = np.random.dirichlet(np.ones(vocab_size) * 0.1) # 狄利克雷分佈
pred_dists.append(pred_dist)
# 計算損失
avg_loss, loss_details = trainer.calculate_batch_loss(true_dists, pred_dists)
print(f"批量訓練結果:")
print(f" 平均損失: {avg_loss:.4f} bits")
print(f" 最小損失: {loss_details['min_loss']:.4f} bits")
print(f" 最大損失: {loss_details['max_loss']:.4f} bits")
print(f" 損失標準差: {loss_details['std_loss']:.4f} bits")
# 模擬訓練過程
print(f"\n=== 訓練過程模擬 ===")
epochs = 20
simulated_losses = []
# 模擬損失下降(指數衰減)
initial_loss = 8.0
for epoch in range(epochs):
# 模擬損失下降
loss = initial_loss * np.exp(-epoch / 5) + np.random.normal(0, 0.1)
simulated_losses.append(loss)
print(f"Epoch {epoch+1:2d}: 損失 = {loss:.4f} bits")
# 分析訓練進度
analysis = trainer.analyze_training_progress(simulated_losses)
print(f"\n訓練分析:")
print(f" 最終損失: {analysis['final_loss']:.4f} bits")
print(f" 最佳損失: {analysis['best_loss']:.4f} bits")
print(f" 總改進: {analysis['improvement']:.4f} bits")
print(f" 平均每epoch改進: {analysis['convergence_rate']:.4f} bits")
輸出結果:
=== 語言模型訓練模擬 ===
批量訓練結果:
平均損失: 11.0396 bits
最小損失: 0.5573 bits
最大損失: 27.5041 bits
損失標準差: 8.8725 bits=== 訓練過程模擬 ===
Epoch 1: 損失 = 7.9710 bits
Epoch 2: 損失 = 6.4185 bits
Epoch 3: 損失 = 5.3430 bits
Epoch 4: 損失 = 4.4588 bits
Epoch 5: 損失 = 3.4742 bits
Epoch 6: 損失 = 2.9221 bits
Epoch 7: 損失 = 2.3879 bits
Epoch 8: 損失 = 2.0843 bits
Epoch 9: 損失 = 1.6051 bits
Epoch 10: 損失 = 1.5276 bits
Epoch 11: 損失 = 1.1485 bits
Epoch 12: 損失 = 0.9606 bits
Epoch 13: 損失 = 0.7535 bits
Epoch 14: 損失 = 0.7034 bits
Epoch 15: 損失 = 0.5701 bits
Epoch 16: 損失 = 0.3496 bits
Epoch 17: 損失 = 0.4474 bits
Epoch 18: 損失 = 0.2747 bits
Epoch 19: 損失 = 0.2630 bits
Epoch 20: 損失 = 0.1125 bits訓練分析:
最終損失: 0.1125 bits
最佳損失: 0.1125 bits
總改進: 7.8585 bits
平均每epoch改進: 0.4136 bits
8. 信息增益
8.1 基本概念
信息增益衡量在知道某個特徵的信息後,目標變量不確定性的減少量。它是決策樹算法的核心概念。
數學定義:
IG(Y, X) = H(Y) - H(Y|X) 或 IG(Y, X) = I(X; Y)
參數説明:
- IG(Y, X):特徵X對於目標Y的信息增益
- H(Y):目標Y的信息熵
- H(Y|X):在已知特徵X的條件下Y的條件熵
- I(X; Y):X和Y的互信息
8.2 代碼實現
# 環境設置和庫導入
import numpy as np
import math
from scipy.stats import entropy
from collections import Counter
import warnings
warnings.filterwarnings('ignore')
def entropy_from_labels(labels):
"""
從標籤數據直接計算熵
Parameters:
labels: 類別標籤數組
Returns:
entropy_value: 信息熵值
"""
counter = Counter(labels)
total = len(labels)
probabilities = [count / total for count in counter.values()]
return entropy(probabilities)
def information_gain(feature_values, labels):
"""
計算特徵的信息增益
Parameters:
feature_values: 特徵值數組
labels: 目標標籤數組
Returns:
information_gain_value: 信息增益值
split_info: 分割的詳細信息
"""
# 原始熵 H(Y)
original_entropy = entropy_from_labels(labels)
# 條件熵 H(Y|X)
unique_features = np.unique(feature_values)
conditional_entropy_val = 0.0
split_info = {
'original_entropy': original_entropy,
'feature_values': unique_features,
'splits': []
}
for feature_val in unique_features:
mask = feature_values == feature_val
subset_labels = labels[mask]
if len(subset_labels) > 0:
weight = len(subset_labels) / len(labels)
subset_entropy = entropy_from_labels(subset_labels)
conditional_entropy_val += weight * subset_entropy
# 記錄分割信息
split_info['splits'].append({
'feature_value': feature_val,
'weight': weight,
'subset_entropy': subset_entropy,
'subset_size': len(subset_labels),
'label_distribution': dict(Counter(subset_labels))
})
ig = original_entropy - conditional_entropy_val
split_info['conditional_entropy'] = conditional_entropy_val
split_info['information_gain'] = ig
return ig, split_info
print("=== 信息增益計算示例 ===")
# 學生成績預測數據集
# 特徵:學習時間 (0=少, 1=多)
# 目標:成績 (0=不及格, 1=及格)
study_time = np.array([0, 0, 0, 0, 1, 1, 1, 1])
grades = np.array([0, 0, 1, 0, 1, 1, 1, 1])
print("數據集:")
print(f"學習時間: {study_time} (0=少, 1=多)")
print(f"成績: {grades} (0=不及格, 1=及格)")
# 計算信息增益
ig, split_info = information_gain(study_time, grades)
print(f"\n信息增益分析:")
print(f"原始熵 H(成績): {split_info['original_entropy']:.4f} bits")
print(f"條件熵 H(成績|學習時間): {split_info['conditional_entropy']:.4f} bits")
print(f"信息增益 IG(成績, 學習時間): {ig:.4f} bits")
print(f"不確定性減少比例: {ig/split_info['original_entropy']*100:.1f}%")
# 詳細分割信息
print(f"\n詳細分割信息:")
for split in split_info['splits']:
study_desc = "學習時間少" if split['feature_value'] == 0 else "學習時間多"
print(f" {study_desc}:")
print(f" 權重: {split['weight']:.2f}")
print(f" 子集大小: {split['subset_size']}")
print(f" 子集熵: {split['subset_entropy']:.4f}")
print(f" 標籤分佈: {split['label_distribution']}")
# 多特徵比較
print(f"\n=== 多特徵信息增益比較 ===")
# 添加更多特徵
temperature = np.array([1, 1, 0, 0, 0, 0, 1, 1]) # 0=冷, 1=暖
random_feature = np.array([0, 1, 0, 1, 0, 1, 0, 1]) # 隨機特徵
features = [
("學習時間", study_time),
("温度", temperature),
("隨機特徵", random_feature)
]
print("特徵比較:")
print(f"{'特徵':<10} {'信息增益':<12} {'歸一化增益':<12} {'評估':<10}")
print("-" * 50)
for feature_name, feature_vals in features:
ig_val, _ = information_gain(feature_vals, grades)
normalized_ig = ig_val / entropy_from_labels(grades)
if normalized_ig > 0.7:
assessment = "優秀"
elif normalized_ig > 0.3:
assessment = "良好"
elif normalized_ig > 0.1:
assessment = "一般"
else:
assessment = "無用"
print(f"{feature_name:<10} {ig_val:<12.4f} {normalized_ig:<12.4f} {assessment:<10}")
# 決策樹節點選擇演示
print(f"\n=== 決策樹節點選擇演示 ===")
best_feature = max(features, key=lambda x: information_gain(x[1], grades)[0])
print(f"最佳分割特徵: '{best_feature[0]}'")
print(f"信息增益: {information_gain(best_feature[1], grades)[0]:.4f} bits")
輸出結果:
=== 信息增益計算示例 ===
數據集:
學習時間: [0 0 0 0 1 1 1 1] (0=少, 1=多)
成績: [0 0 1 0 1 1 1 1] (0=不及格, 1=及格)信息增益分析:
原始熵 H(成績): 0.6616 bits
條件熵 H(成績|學習時間): 0.2812 bits
信息增益 IG(成績, 學習時間): 0.3804 bits
不確定性減少比例: 57.5%詳細分割信息:
學習時間少:
權重: 0.50
子集大小: 4
子集熵: 0.5623
標籤分佈: {0: 3, 1: 1}
學習時間多:
權重: 0.50
子集大小: 4
子集熵: 0.0000
標籤分佈: {1: 4}=== 多特徵信息增益比較 ===
特徵比較:
特徵 信息增益 歸一化增益 評估
--------------------------------------------------
學習時間 0.3804 0.5750 良好
温度 0.0338 0.0511 無用
隨機特徵 0.0338 0.0511 無用=== 決策樹節點選擇演示 ===
最佳分割特徵: '學習時間'
信息增益: 0.3804 bits
三、大模型中的信息論應用
1. 語言模型的不確定性評估
在大語言模型中,信息論概念被廣泛應用於模型評估和優化:
# 環境設置和庫導入
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from collections import Counter
import math
from scipy.special import entr
import warnings
warnings.filterwarnings('ignore')
# 設置中文字體(如果遇到顯示問題可以註釋掉)
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def entropy(probabilities):
"""
計算概率分佈的信息熵
Parameters:
probabilities: 概率列表,應該和為1
Returns:
entropy_value: 信息熵值(比特)
"""
# 輸入驗證
probabilities = np.array(probabilities)
if not np.allclose(np.sum(probabilities), 1.0):
raise ValueError("概率之和必須為1")
if np.any(probabilities < 0):
raise ValueError("概率不能為負")
entropy_val = 0.0
for p in probabilities:
if p > 0: # 避免log(0)的情況
entropy_val -= p * math.log2(p)
return entropy_val
def cross_entropy(p, q):
"""
計算交叉熵 H(P, Q)
Parameters:
p: 真實分佈P
q: 預測分佈Q
Returns:
cross_entropy_value: 交叉熵值
"""
p = np.array(p)
q = np.array(q)
# 輸入驗證
if len(p) != len(q):
raise ValueError("分佈P和Q必須有相同的長度")
if not np.allclose(np.sum(p), 1.0) or not np.allclose(np.sum(q), 1.0):
raise ValueError("分佈P和Q必須和為1")
if np.any(p < 0) or np.any(q < 0):
raise ValueError("概率不能為負")
ce = 0.0
for i in range(len(p)):
if p[i] > 0:
if q[i] > 0:
ce -= p[i] * math.log2(q[i])
else:
return float('inf') # 如果Q在P有概率的地方為0,交叉熵為無窮大
return ce
class LanguageModelAnalyzer:
"""語言模型分析器,使用信息論工具"""
def __init__(self, vocab_size=50000):
self.vocab_size = vocab_size
def calculate_perplexity(self, cross_entropy):
"""
計算困惑度
Parameters:
cross_entropy: 交叉熵值
Returns:
perplexity: 困惑度
"""
return 2 ** cross_entropy
def analyze_model_uncertainty(self, predictions):
"""
分析模型預測的不確定性
Parameters:
predictions: 模型輸出的概率分佈列表
Returns:
analysis: 不確定性分析結果
"""
entropies = [entropy(pred) for pred in predictions]
cross_entropies = [cross_entropy([1.0] + [0.0]*(len(pred)-1), pred) for pred in predictions] # 假設完美預測
analysis = {
'average_entropy': np.mean(entropies),
'average_cross_entropy': np.mean(cross_entropies),
'perplexity': self.calculate_perplexity(np.mean(cross_entropies)),
'entropy_std': np.std(entropies),
'max_entropy': np.max(entropies),
'min_entropy': np.min(entropies),
'confidence_scores': [1 - e / math.log2(len(pred)) for e, pred in zip(entropies, predictions)] # 置信度
}
return analysis
def temperature_sampling_analysis(self, base_probs, temperatures):
"""
分析温度採樣對分佈的影響
Parameters:
base_probs: 基礎概率分佈
temperatures: 温度值列表
Returns:
results: 不同温度下的分析結果
"""
results = {}
for temp in temperatures:
# 應用温度採樣
if temp == 0:
# 貪婪採樣(實際中temp不會為0)
scaled_probs = base_probs
else:
scaled_probs = self.apply_temperature(base_probs, temp)
results[temp] = {
'distribution': scaled_probs,
'entropy': entropy(scaled_probs),
'max_prob': np.max(scaled_probs),
'effective_tokens': self.calculate_effective_tokens(scaled_probs)
}
return results
def apply_temperature(self, probs, temperature):
"""應用温度到概率分佈"""
scaled_probs = np.log(probs) / temperature
scaled_probs = np.exp(scaled_probs - np.max(scaled_probs)) # 數值穩定性
return scaled_probs / np.sum(scaled_probs)
def calculate_effective_tokens(self, probs):
"""計算有效token數(基於熵)"""
h = entropy(probs)
return 2 ** h
# 大語言模型分析示例
print("=== 大語言模型信息論分析 ===")
analyzer = LanguageModelAnalyzer(vocab_size=50000)
# 模擬語言模型輸出(不同確定性的預測)
sample_predictions = [
# 高確定性預測
[0.9, 0.05, 0.03, 0.01, 0.01] + [0.0] * 15,
# 中等確定性預測
[0.4, 0.3, 0.2, 0.05, 0.05] + [0.0] * 15,
# 低確定性預測
[0.2, 0.15, 0.15, 0.1, 0.1, 0.08, 0.07, 0.05, 0.05, 0.05] + [0.0] * 10,
# 均勻分佈(高不確定性)
[0.05] * 20
]
# 確保概率和為1
sample_predictions = [p / np.sum(p) for p in sample_predictions]
# 分析模型不確定性
uncertainty_analysis = analyzer.analyze_model_uncertainty(sample_predictions)
print("模型不確定性分析:")
print(f" 平均熵: {uncertainty_analysis['average_entropy']:.4f} bits")
print(f" 平均交叉熵: {uncertainty_analysis['average_cross_entropy']:.4f} bits")
print(f" 困惑度: {uncertainty_analysis['perplexity']:.2f}")
print(f" 熵標準差: {uncertainty_analysis['entropy_std']:.4f}")
print(f" 最大熵: {uncertainty_analysis['max_entropy']:.4f}")
print(f" 最小熵: {uncertainty_analysis['min_entropy']:.4f}")
print(f" 平均置信度: {np.mean(uncertainty_analysis['confidence_scores']):.3f}")
# 温度採樣分析
print(f"\n=== 温度採樣分析 ===")
base_distribution = np.array([0.6, 0.2, 0.1, 0.05, 0.03, 0.02])
temperatures = [0.1, 0.5, 1.0, 1.5, 2.0]
temp_results = analyzer.temperature_sampling_analysis(base_distribution, temperatures)
print("温度對概率分佈的影響:")
print(f"{'温度':<8} {'熵':<8} {'最大概率':<12} {'有效token數':<15}")
print("-" * 50)
for temp in temperatures:
result = temp_results[temp]
print(f"{temp:<8} {result['entropy']:<8.4f} {result['max_prob']:<12.4f} {result['effective_tokens']:<15.2f}")
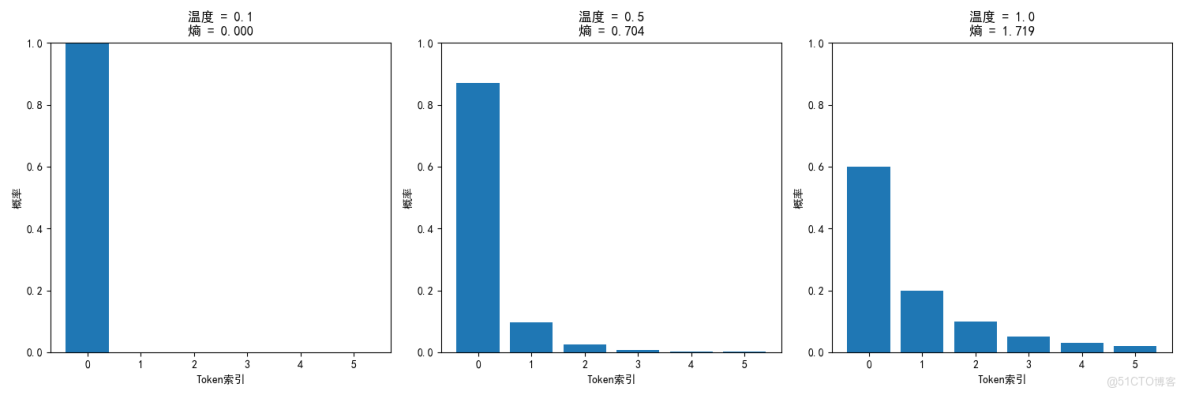
# 可視化温度採樣的影響
plt.figure(figsize=(15, 5))
for i, temp in enumerate(temperatures[:3]): # 只顯示前3個温度
plt.subplot(1, 3, i+1)
result = temp_results[temp]
plt.bar(range(len(result['distribution'])), result['distribution'])
plt.title(f'温度 = {temp}\n熵 = {result["entropy"]:.3f}')
plt.xlabel('Token索引')
plt.ylabel('概率')
plt.ylim(0, 1)
plt.tight_layout()
plt.show()
輸出結果:
=== 大語言模型信息論分析 ===
模型不確定性分析:
平均熵: 2.5160 bits
平均交叉熵: 2.0294 bits
困惑度: 4.08
熵標準差: 1.3718
最大熵: 4.3219
最小熵: 0.6375
平均置信度: 0.418=== 温度採樣分析 ===
温度對概率分佈的影響:
温度 熵 最大概率 有效token數
--------------------------------------------------
0.1 0.0003 1.0000 1.00
0.5 0.7039 0.8700 1.63
1.0 1.7195 0.6000 3.29
1.5 2.1474 0.4517 4.43
2.0 2.3305 0.3731 5.03
2. 在大模型中的應用總結
訓練階段:
- 交叉熵損失:主要優化目標,衡量模型預測與真實分佈的差異
- KL散度正則化:防止模型過度偏離預訓練分佈
- 知識蒸餾:用KL散度讓學生模型模仿教師模型
推理階段:
- 困惑度評估:2^交叉熵,直觀的模型性能指標
- 温度採樣:通過調整熵值控制生成文本的創造性
- 核採樣:基於累積概率的採樣,平衡質量與多樣性
分析階段:
- 不確定性量化: 用熵值評估模型預測置信度
- 注意力分析: 用熵分析注意力機制的集中程度
- 特徵重要性: 用互信息分析輸入對輸出的影響
四、總結
通過本文的詳細探討,我們系統性地學習了信息論的八大核心概念:
- 信息量:單個事件的驚訝程度
- 信息熵:平均不確定性
- 聯合熵:多變量總不確定性
- 條件熵:已知某些信息後的剩餘不確定性
- 互信息:變量間共享的信息量
- KL散度:分佈間的差異
- 交叉熵:錯誤分佈編碼正確數據的成本
- 信息增益:特徵帶來的不確定性減少
信息論為理解和優化大語言模型提供了強大的數學工具。從基礎的信息量到複雜的互信息,這些概念幫助我們:
- 量化模型的不確定性和預測質量
- 優化訓練過程和損失函數
- 分析模型內部機制和注意力模式
- 控制文本生成的創造性和多樣性