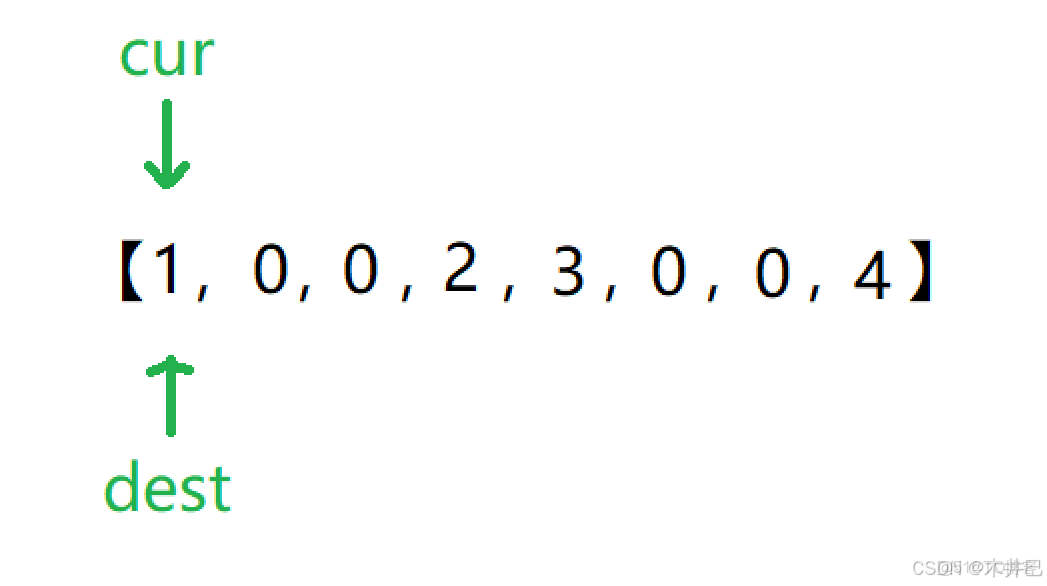目錄

一、雙指針簡介

對撞指針

快慢指針

二、OJ題目

2.1 移動零

算法設計

代碼實現

算法總結

2.2 複寫零

算法設計

代碼實現

算法總結

2.3 快樂數

算法設計

代碼實現

算法總結

2.4 盛最多水的容器

算法設計

代碼實現

算法總結

2.5 有效三角形的個數

算法設計

代碼實現

算法總結

2.6 查找總價格為目標值的兩個商品（兩數之和）

算法設計

代碼實現

算法總結

2.7 三數之和

算法設計

代碼實現

算法總結

2.8 四數之和

算法設計

代碼實現

算法總結

一、雙指針簡介

常見的雙指針有兩種形式：對撞指針 和 快慢指針 。

對撞指針

也稱左右指針，一般用於順序結構中。

特點：一個指針在最左邊位置，一個指針在最右邊位置，兩個指針逐漸往中間走，直到相遇或者錯開就停止。

快慢指針

也稱前後指針， 其基本思想就是使用兩個移動速度不同的指針在數組或鏈表等序列結構上移動。

特點：通常用於處理 環形鏈表 或 數組 或者其他 出現循壞往復情況 的問題，最常用的方式是讓慢指針每一次移動一位，讓快指針每一次移動兩位。

二、OJ題目

2.1 移動零

算法設計

根據題目的示例1分析，我們可以發現：

結果分為兩個部分：一部分全是非零元素，一部分全是零

這兩個部分將整個數組分塊了，那我們就可以使用雙指針來劃分。

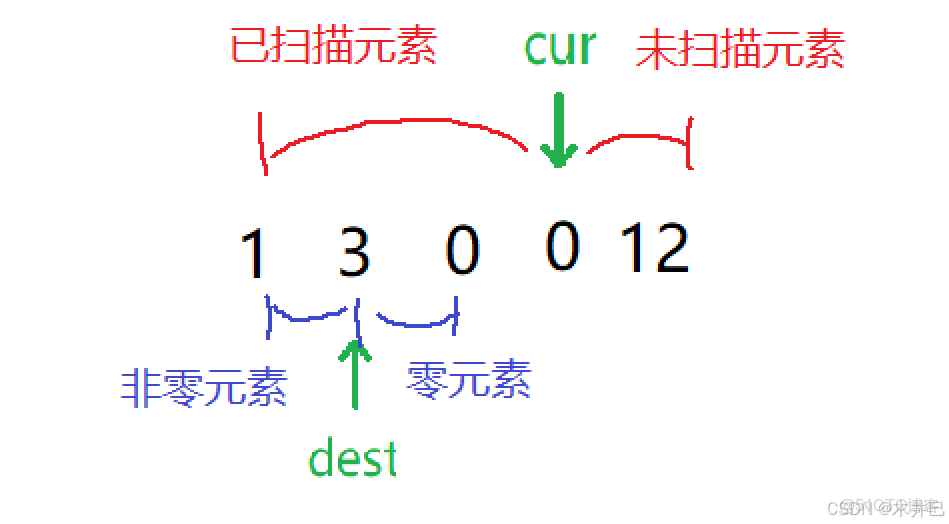
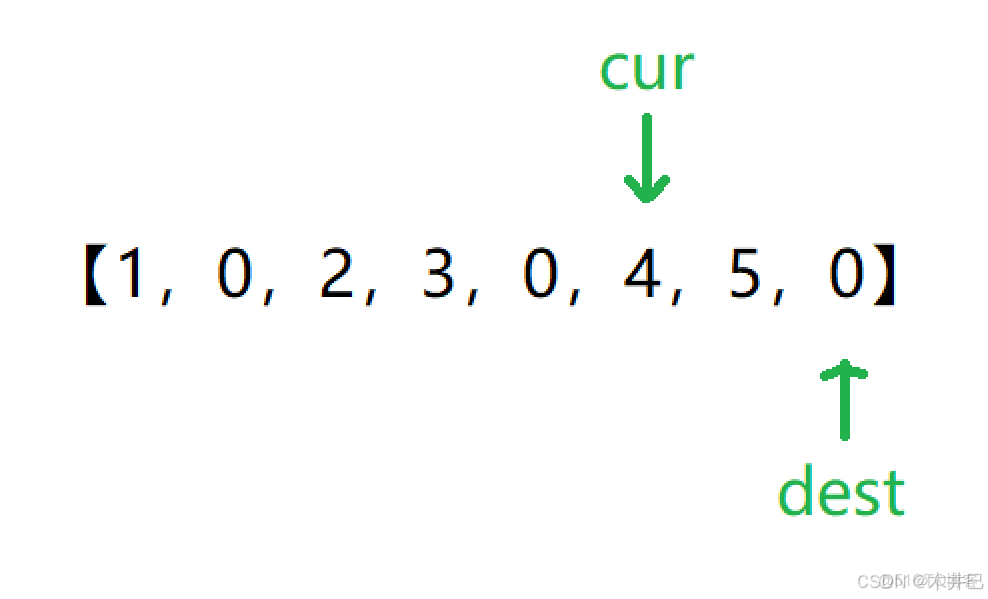
定義兩個指針 cur 和 dest ，其中 cur 指針用來掃描數組，它的左邊是已掃描的部分，右邊是未掃描的部分；dest 指針充當非零元素部分和零元素部分的分界，而這兩個部分又包含在已掃描部分中，因此操作的過程中數組被 cur 和 dest 分為三個部分：非零元素部分、零元素部分和未掃描元素部分。

當 cur 掃描完整個數組必會越界，此時操作就完成了，整個數組被 dest 分為兩個部分：非零元素部分和零元素部分。

從以上分析可以看出，我們使用的是快慢指針來解決這道問題。

具體操作如下：

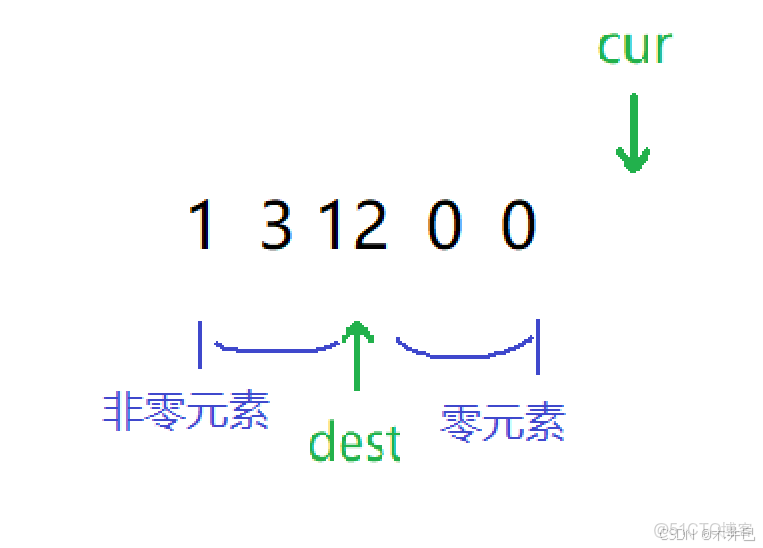
1. 先初始化雙指針：cur 在下標為0的位置，dest 暫時不讓它進入數組，給一個-1。（即 cur = 0, dest = -1）

2. 然後我們讓 cur指針開始遍歷掃描數組：當 cur 還未越界時，我們就判斷一下 nums[cur] 這個元素是否為零：

        1. 若不為零，我們就讓 nums[dest+1] 和 nums[cur] 進行交換；

        2. 若為零，就讓 cur 繼續掃描數組。

3. 當 cur 越界，就結束操作。

讀者可以自行模擬以上操作，看看所得結果是否滿足題目要求。

代碼實現

public void moveZeroes(int[] nums) {
    int cur = 0, dest = -1;
    while (cur < nums.length) {
        if (nums[cur] != 0) {
            swap(nums,++dest,cur++);
        } else {
            cur++;
        }
    }
}
private void swap(int[] nums, int i, int j) {
    int temp = nums[i];
    nums[i] = nums[j];
    nums[j] = temp;
}

提交結果：

算法總結

這道題目的特點是 數組分塊 ，因此以後我們刷題時遇到類似題目時，可以採用此題的算法思路結合題目具體細節來解決問題。

2.2 複寫零

算法設計

我們採用快慢指針來解決這道問題：cur指針用於檢查元素是否為零；dest指針用於複寫操作。

具體如下：

1. 初始化雙指針：cur 置於下標為0的位置，dest 初始化為-1；

2. 遍歷數組進行復寫操作：

        1. 當 arr[cur] 不為零：將 arr[cur] 複寫至 arr[dest+1]；

        2. 當 arr[cur] 為零：進行兩次 arr[++dest] = 0 操作。

3. 當 cur 越界，操作就結束。

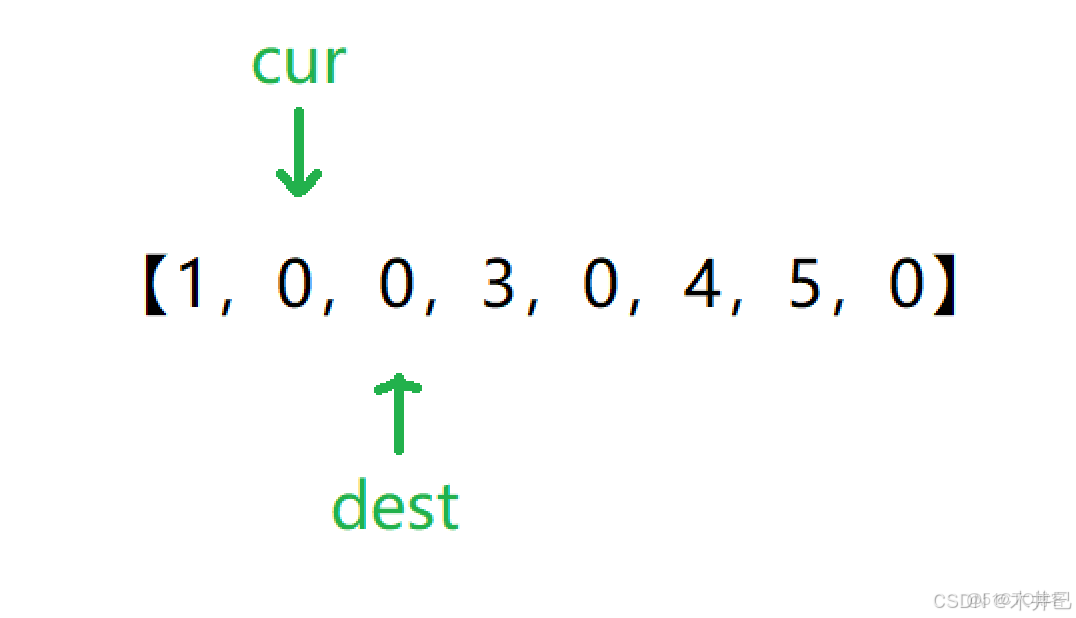
但是，當我們根據示例1從前往後進行模擬複寫操作時，會發現有些元素會被覆蓋：

原數組中下標為2的元素2被覆蓋了，這意味着往後再怎麼複寫這個答案都是錯的，因為有數據丟失。

因此，按照從前往後的方法不可行，那從後往前呢？

我們觀察示例1，可以發現最後一個複寫的元素是4，那我們不妨將 cur 置於元素4，將 dest 置於數組最後位置

接下來從後往前模擬複寫操作（思路一致，只不過方向不同，'+' 號改 '-' 號即可），

可以發現，結果正確，説明從後往前複寫的方法是正確的。

那麼這道題目的解題步驟就是：

1. 首先找到每一個測試用例的最後複寫的元素

2. 然後進行復寫操作。

那麼問題來了，我們是通過觀察示例1才得知最後複寫的元素，計算機可不會觀察。

那怎麼找呢？

具體如下：

1. cur = 0, dest = -1；

2. cur 遍歷數組：

        1. 當 arr[cur] 不為零，dest++ 即可；

        2. 當 arr[cur] 為零，dest += 2。

3. 在 cur++ 之前，我們首先要判斷一下 dest 的位置是否越界（因為當 arr[cur] 是零時，dest 的位置經過操作後可能會越界：示例 [1,0,2,3,0,4] ）:

        1. 若 dest == arr.length：此時複寫的兩個零的位置是 arr.length-1 和 arr.length，

        由於 dest 等於 arr.length 時已越界，我們不管，只需要將 arr[arr.length-1] 改成0，

        2. 然後再讓 cur--，dest -= 2即可。

經過以上三步的操作，我們就可以找到每一個測試用例的最後複寫的元素，接下來進行復寫操作即可。

讀者可自行模擬操作。

代碼實現

public void duplicateZeros(int[] arr) {
    int cur = 0, dest = -1;
    int n = arr.length;
    // 1. 找到最後複寫的數
    while (cur < n) {
        if (arr[cur] == 0) {
            dest += 2;
        } else {
            dest++;
        }
        // 判斷dest位置是否越界
        if (dest >= n-1) {
            break;
        }
        cur++;
    }
    // 處理細節
    if (dest == n) {  // 導致這種情況必是因為arr[cur]為0
        // 只將arr[n-1]改成0即可
        arr[n-1] = 0;
        cur--;
        dest -= 2;
    }
    // 2. 從後往前複寫
    while (cur >= 0) {
        if (arr[cur] != 0) {
            arr[dest--] = arr[cur--];
        } else {
            arr[dest--] = 0;
            arr[dest--] = 0;
            cur--;
        }
    }
}

提交結果

算法總結

這道題目需要轉變一下思路，既然從前往後行不通，那就從後往前。其原因就是按原來的方法會有數據被覆蓋，因此當以後遇到類似的題目，我們可以採用這道題目的思路。

2.3 快樂數

算法設計

由題目描述我們可以知道，驗證快樂數操作是一直重複的：

1. 最終結果始終無限循環變不到1，

2. 最終結果是1（我們可以看作重複操作但結果一直是1）

對示例1進行模擬操作：

對於這種情況，我們可以使用 快慢指針 的方法解決這道題：

1. 初始化雙指針：先將 slow 置為 n ，將 fast 置為 slow 後的元素（即經過一次操作後得到的數）；

2. 讓 slow 每一次走一個位置，fast 每一次走兩個位置；

3. 當兩個指針相遇，判斷所處位置的值：

        1. 若所處位置的值為1，表示 n 是快樂數，返回 true；

        2. 若所處位置的值不為1，表示 n 是快樂數，返回 false。

這種操作是不是有點似曾相識的感覺？本題與 判斷鏈表中是否有環 一題的解法是如出一轍。

讀者可以自行模擬以上操作。

代碼實現

public boolean isHappy(int n) {
    int slow = n, fast = isHappyNum(n);
    while (slow != fast) {
        slow = isHappyNum(slow);
        fast = isHappyNum(isHappyNum(fast));
    }
    return (slow == 1) ? true : false;
}
private int isHappyNum(int n) {
    int temp = 0, ret = 0;
    while (n > 0) {
        temp = n % 10;
        n /= 10;
        ret += temp * temp;
    }
    return ret;
}

提交結果

算法總結

本題的特點是出現循環、重複某個操作，因此採用 快慢指針 的方法來解決，以後遇到此類相似問題，我們也可以採用這種算法思路來解決。

2.4 盛最多水的容器

算法設計

根據題目描述，我們需要返回面積的最大值，

面積計算方式如下：S = (right - left) * min( height[left], hright[right] )

最簡單的解法就是將所有可能的面積都求出來，然後比較哪一個最大，返回最大的面積即可。

解法一：暴力枚舉

1. 使用兩個指針，left 遍歷數組，每次固定一個數，然後 right 逐一遍歷數組，將每一個數與 left 所固定的數組合並求出面積；

2. 當 right 遍歷完數組，left 再向後走一位，right 回到 left 的位置重新開始遍歷操作。

3. 將得到的最大面積返回即可。

但是，當我們把代碼提交，可以發現這種解法會超時。

我們從面積計算公式來看：

v = h (高)  * w (寬)

1. 當 h 最高且 w 最寬時，整個面積是最大的；

2. 當 h 不變且 w 減少時 或者 當 h 減少且 w 減少時，面積都不是最大的。

我們能否從兩端開始尋找呢？當找到最高的 h ，w 也是最大的。

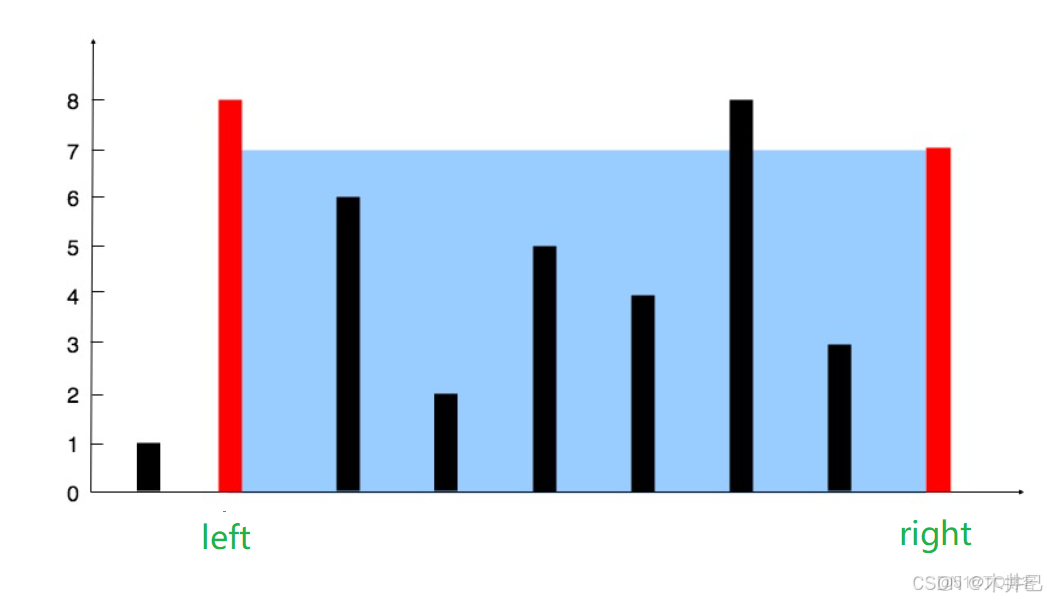
解法二：雙指針（對撞指針）

1. 先初始化指針：將 left 置於下標為0的位置，將 right 置於數組最後位置；

2. 用一個變量 maxArea 存放最大面積，計算以 left 和 right 為兩邊的容器的面積並更新 maxArea

3. 接下來讓 left 和 right 逐漸往中間走：判斷左右兩條邊那個更短，若左邊更短，left ++；若右邊更短，right --，計算新的面積並更新 maxArea

4. 當 left 和 right 相遇，返回結果即可

讀者可以自行模擬以上操作

代碼實現

public int maxArea(int[] height) {
    int left = 0;
    int right = height.length - 1;
    int v = 0;
    int maxArea = 0;
    // 雙指針從兩邊到中間找容積最大的
    while (left < right) {
        v = Math.min(height[left], height[right]) * (right - left);
        maxArea = Math.max(maxArea, v);
        if (height[left] < height[right]) {
            left++;
        } else {
            right--;
        }
    }
    //  返回最大容積
    return max;
}

算法總結

這道題目使用 對撞指針

2.5 有效三角形的個數

算法設計

解法一：暴力枚舉（會超時）

最容易想的解法就是將所有的三元組全部列出來，然後看看哪些能夠構成三角形。

轉換成代碼就是需要三層循環來實現，時間複雜度能夠達到 O（N³）。

最開始讓 i 置於下標為0的位置，j 位於 i+1 位置，k 位於 j+1 位置，然後逐一遍歷判斷。

很顯然，這種解法太耗時，我們需要優化一下。

解法二：雙指針（排序 + 對撞指針）

我們知道，構成三角形的條件是：任意兩邊之和大於第三邊，

我們這個解法之所以用時長是因為我們需要找三個數，

如果我們將問題轉化成：找到兩個數他們的和大於一個固定的數，那麼我們就可以減少時間的消耗，從而提高效率。

我們可以這樣做：將數組排列成有序數組（利用有序數組的單調性），然後直接找到最大的數（固定的數），再在前面的區間中找到兩個數的和大於該固定的數，再固定下一個最大的數循環操作。

具體步驟：

1. 先將數組排序。

2. 我們固定一個 最大數 i ，再在 [0, i - 1] 這個區間中找出兩個和大於該最大數的數（二元組），

3. 我們定義雙指針 left = 0，right = i - 1，則在區間 [left, right]中：

        1. 若 nums[left] + nums[right] > nums[i] ：

                · 由於 left 是區間內最小的數，left + right 的值都大於 i 了，那區間內其他數肯定也滿足要求（即區間 [left + 1, right]）。

                · 計算滿足條件的三元組的個數：right -  left。

                · 此時 right 位置元素的所有情況已經考慮完了，我們需要 right--，繼續下一輪的操作。

        2. 若 nums[left] + nums[right] <= nums[i] ：

                · 由於 right 是區間內最大的數，left + right 的值都小於等於 i 了，那區間內其他數肯定也是小於或等於 i 的（即區間 [left, right - 1]）。

                · 此時將 left++，進入下一輪的操作。

4. 操作結束後，返回統計到的三元組的個數即可。

該解法的時間複雜度是 O（N²）。

讀者可以通過畫圖工具自行模擬以上操作。

代碼實現

public int triangleNumber(int[] nums) {
    int ret = 0, left = 0, right = 0, n = nums.length;
    // 1.對數據進行排序
    Arrays.sort(nums);
    // 2.統計有效的三元組的個數
    for (int i = n - 1; i >= 2; i--) {
        left = 0; right = i - 1;
        while (left < right) {
            if (nums[left] + nums[right] > nums[i]) {
                ret += right - left;
                right--;
            } else {
                left++;
            }
        }
    }
    return ret;
}

算法總結

這道題目中利用了有序數組的單調性得以實現效率的提升，有時候 單調性 是很重要的特性，在以後遇見的題目中要時刻留意是否有單調性這一特性。

2.6 查找總價格為目標值的兩個商品（兩數之和）

算法設計

解法一：暴力枚舉

最簡單的做法就是使用兩層循環遍歷數組找到兩個數，但是會超時。

解法二：對撞指針

注意到數組是升序排列的數組，我們可以使用對撞指針來解決。

步驟如下：

1. 初始化雙指針：left = 0，right = n - 1（這裏的 n 是數組的長度）。

2. 當 left 小於 right 的時候，就一直循環以下操作：

        1. 當 price[left] + price[right] > target：

                · 由於 left 是區間 [left, right] 中最小的數，最小的數與區間內最大的數 right 相加都大於 target 了，那麼比 left 還大的數與 right 相加肯定更大了。因此沒有必要從區間 [left + 1, right] 中查找了，我們直接讓最大的數 right-- 即可。

        2. 當 price[left] + price[right] < target：

                · 由於 right 是區間 [left, right] 中最大的數，最大的數與區間內最小的數 left 相加都小於 target 了，那麼比 right 還小的數與 left 相加肯定更小了。因此沒有必要從區間 [left , right - 1] 中查找了，我們直接讓最小的數 left++ 即可。

        3. 當 price[left] + price[right] == target：

                · 找到目標數，我們返回結果即可。

3. 若操作結束都沒有返回結果，説明數組中不存在滿足要求的數，返回 null。

代碼實現

public int[] twoSum(int[] price, int target) {
    int n = price.length, left = 0, right = n - 1;
    // 雙指針遍歷數組查找
    while (left < right) {
        if (price[left] + price[right] > target) {
            right--;
        } else if (price[left] + price[right] < target) {
            left++;
        } else {
            return new int[] {price[left] , price[right]};
        }
    }
    return null;
}

算法總結

我覺得這道題目是很有代表性的一道題目，經典的按照三種不同的情況來討論，細節問題不多。後面還會有題目有更多細節需要處理。

2.7 三數之和

算法設計

解法一：排序 + 暴力枚舉 + set 去重

這個代碼需要使用三層循環來尋找三元組，是比較耗時的解法。

解法二：排序 + 雙指針

整體思路和兩數之和的思路差不多，只不過有些細節需要處理。

我們可以將三個數問題轉化成兩個數問題：

先固定一個數 a ，在剩下的數中找到和為 -a 的兩個數，這樣一來就轉化為兩數之和問題了。

題目要求 “不重複”，因此我們需要對滿足條件的三元組進行“去重操作”。

具體步驟：

1. 對數組進行排序。

2. 先固定一個數 a ，在剩下的數中找到和為 -a 的兩個數（使用對撞指針 left 和 right）：

        · 若 nums[left] + nums[right] > -a：

        直接讓 right --

        · 若 nums[left] + nums[right] < -a：

        直接讓 left ++

        · 若 nums[left] + nums[right] == -a：

        記錄下該三元組，然後縮小範圍繼續下一輪的操作（left ++，right --）

3. 當操作完成，返回最終結果即可。

處理細節問題：

1. left 和 right 的去重操作：

        在縮小範圍之後，left 和 right 下一個位置的數可能會與之前的數重複，這時候我們需要判斷一下是否與之前所處位置的數相等，若相等就再走一步（即再執行一次 left ++ 和 right --）。當然也不能一直執行，需要確保不越界（即 left < right ）才可以繼續執行，否則就停止。

2. 固定的第三個數 a 的去重操作：

        因為我們的 a 也是在遍歷數組的，每固定一個數就開始一輪雙指針查找。如果固定的數 a 重複的話，查找得到的三元組也會重複，這樣就不符合題意了。因此，我們需要對 a 也進行去重操作，同時 i 也不能越界。

代碼實現

public List> threeSum(int[] nums) {
    List> ret = new ArrayList<>();
    int i = 0, left = 0, right = 0;
    int n = nums.length;
    // 1. 對數組進行排序
    Arrays.sort(nums);
    // 2. 使用雙指針算法尋找三元組
    // 固定數
    while (i < n) {
        left = i + 1; right = n - 1;
        int t = -nums[i];
        // 在 [left, right] 範圍內尋找和為t的兩個數
        while (left < right) {
            if (nums[left] + nums[right] > t) {
                right--;
            } else if (nums[left] + nums[right] < t) {
                left++;
            } else {
                // 將找到的三元組通過Arrays集合類的asList方法轉換為List，然後用尾插法插入ret
                ret.add(Arrays.asList(nums[i],nums[left],nums[right]));
                // 縮小下一次尋找的範圍
                left++;
                right--;
                // 對left和right進行去重操作（注意不要越界）
                while (left

算法總結再次體現了 “兩數之和” 這道經典題目的重要性~~完

算法總結本題是由經典的 “求兩數之和” 題目衍生而來的，其解題的核心仍然是利用雙指針。2.8 四數之和算法設計解法一：排序 + 暴力枚舉 + set去重和上一道題目一樣，不過這次多了一層循環，即需要四層循環。解法二：排序 + 雙指針這道題目我們可以沿用上一道題目 “三數之和” 的思路，先把四個數問題轉化成三個數問題，再將三個數問題轉化為兩個數問題。具體步驟：1. 依次固定一個數 a ，在剩下的數中找到三個數和為 t - a。2. 再依次固定第二個數 b ，在剩下的數中找到兩個數和為 t - a - b。3. 返回最終結果即可。細節處理：這道題目同樣涉及到去重操作，因此我們也需要對固定的數 a、b，以及雙指針 left 和 right 進行去重操作。代碼實現public List> fourSum(int[] nums, int target) {
    List> ret = new ArrayList<>();
    int i = 0, j = 0, left = 0, right = 0;
    int n = nums.length;
    // 1. 將數據排序
    Arrays.sort(nums);
    // 2. 使用雙指針算法
    while (i < n) {
        // 特殊情況處理
        if (target<0 && nums[0]>=0) {
            return ret;
        }
        // 找到三個數，和為target - nums[i]
        j = i + 1;
        // 使用long類型防止數據溢出
        long t1 = target - nums[i];
        while (j < n) {
            long t2 = t1 - nums[j];
            left = j + 1;
            right = n - 1;
            // 找到兩個數，和為target - nums[i] - nums[j]
            while (left < right) {
                if (nums[left] + nums[right] > t2) {
                    right--;
                } else if (nums[left] + nums[right] < t2) {
                    left++;
                } else {
                    ret.add(Arrays.asList(nums[i], nums[j], nums[left], nums[right]));
                    // 縮小搜尋範圍
                    left++;
                    right--;
                    // 對left和right進行去重操作
                    while (left < right && nums[left] == nums[left - 1]) {
                        left++;
                    }
                    while (left < right && nums[right] == nums[right + 1]) {
                        right--;
                    }
                }
            }
            // 對j進行去重操作
            j++;
            while (j < n && nums[j] == nums[j - 1]) {
                j++;
            }
        }
        // 對i進行去重操作
        i++;
        while (i < n && nums[i] == nums[i - 1]) {
            i++;
        }
    }
    // 3. 返回最終結果
    return ret;
}