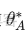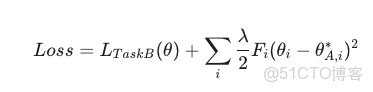import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
import copy

# ===========================
# 1. 定義一個簡單的神經網絡
# ===========================
class SimpleNet(nn.Module):
    def __init__(self):
        super(SimpleNet, self).__init__()
        # 為了演示，我們用一個小型的網絡
        self.fc1 = nn.Linear(10, 20)
        self.fc2 = nn.Linear(20, 20)
        self.fc3 = nn.Linear(20, 2) # 輸出2類

    def forward(self, x):
        x = torch.relu(self.fc1(x))
        x = torch.relu(self.fc2(x))
        return self.fc3(x)

# ===========================
# 2. EWC 核心類 (The Magic)
# ===========================
class EWC:
    def __init__(self, model, dataset):
        self.model = model
        self.dataset = dataset
        # 存儲舊任務的最優參數 (theta_A*)
        self.params = {n: p.data.clone() for n, p in self.model.named_parameters()}
        # 存儲每個參數的重要性 (Fisher Information)
        self.fisher = self._calculate_fisher()

    def _calculate_fisher(self):
        fisher = {}
        # 初始化 Fisher 矩陣為 0
        for n, p in self.model.named_parameters():
            fisher[n] = torch.zeros_like(p.data)

        self.model.eval（)
        criterion = nn.CrossEntropyLoss()
        
        # 遍歷數據計算梯度的平方
        # 這裏的邏輯是：梯度越大，説明參數稍微一動 Loss 變化就大 -> 參數越重要
        for input_data, target in self.dataset:
            self.model.zero_grad()
            output = self.model(input_data.unsqueeze(0)) # batch_size=1
            loss = criterion(output, target.unsqueeze(0))
            loss.backward()

            for n, p in self.model.named_parameters():
                if p.grad is not None:
                    # Fisher 近似等於 梯度的平方
                    fisher[n] += p.grad.data ** 2
        
        # 歸一化
        for n in fisher:
            fisher[n] /= len(self.dataset)
            
        return fisher

    def penalty(self, new_model):
        loss = 0
        for n, p in new_model.named_parameters():
            # EWC 公式: Sum( F * (new_theta - old_theta)^2 )
            _loss = self.fisher[n] * (p - self.params[n]) ** 2
            loss += _loss.sum()
        return loss

# ===========================
# 3. 模擬訓練流程
# ===========================
def get_data(task_id):
    # 模擬數據：Task 1 輸入全1，Task 2 輸入全0
    if task_id == 1:
        return [(torch.ones(10), torch.tensor(0)) for _ in range(100)]
    else:
        return [(torch.zeros(10), torch.tensor(1)) for _ in range(100)]

# 實例化模型
model = SimpleNet()
optimizer = optim.SGD(model.parameters(), lr=0.1)
criterion = nn.CrossEntropyLoss()

print(">>> 開始訓練 任務 A (識別全1向量)")
data_a = get_data(1)
for epoch in range(5):
    for x, y in data_a:
        optimizer.zero_grad()
        loss = criterion(model(x.unsqueeze(0)), y.unsqueeze(0))
        loss.backward()
        optimizer.step()

print("任務 A 訓練完成。保存 EWC 狀態...")
# --- 關鍵步驟：計算 Task A 的重要性權重 ---
ewc = EWC(model, data_a) 

print(">>> 開始訓練 任務 B (識別全0向量)，同時開啓 EWC 保護")
data_b = get_data(2)
ewc_lambda = 1000  # 懲罰力度，越大越照顧舊任務

for epoch in range(5):
    total_loss = 0
    for x, y in data_b:
        optimizer.zero_grad()
        
        # 1. 計算新任務的 Loss
        loss_b = criterion(model(x.unsqueeze(0)), y.unsqueeze(0))
        
        # 2. 計算 EWC 懲罰項 (舊任務的記憶)
        loss_ewc = ewc.penalty(model)
        
        # 3. 總 Loss
        loss = loss_b + (ewc_lambda * loss_ewc)
        
        loss.backward()
        optimizer.step()
        total_loss += loss.item()
    print(f"Epoch {epoch}: Loss = {total_loss:.4f}")

# ===========================
# 4. 驗證結果
# ===========================
model.eval（)
test_a = model(torch.ones(10).unsqueeze(0))
test_b = model(torch.zeros(10).unsqueeze(0))

print("\n=== 最終測試 ===")
print(f"Task A (應為類別0): 預測概率 {torch.softmax(test_a, dim=1).detach().numpy()}")
print(f"Task B (應為類別1): 預測概率 {torch.softmax(test_b, dim=1).detach().numpy()}")