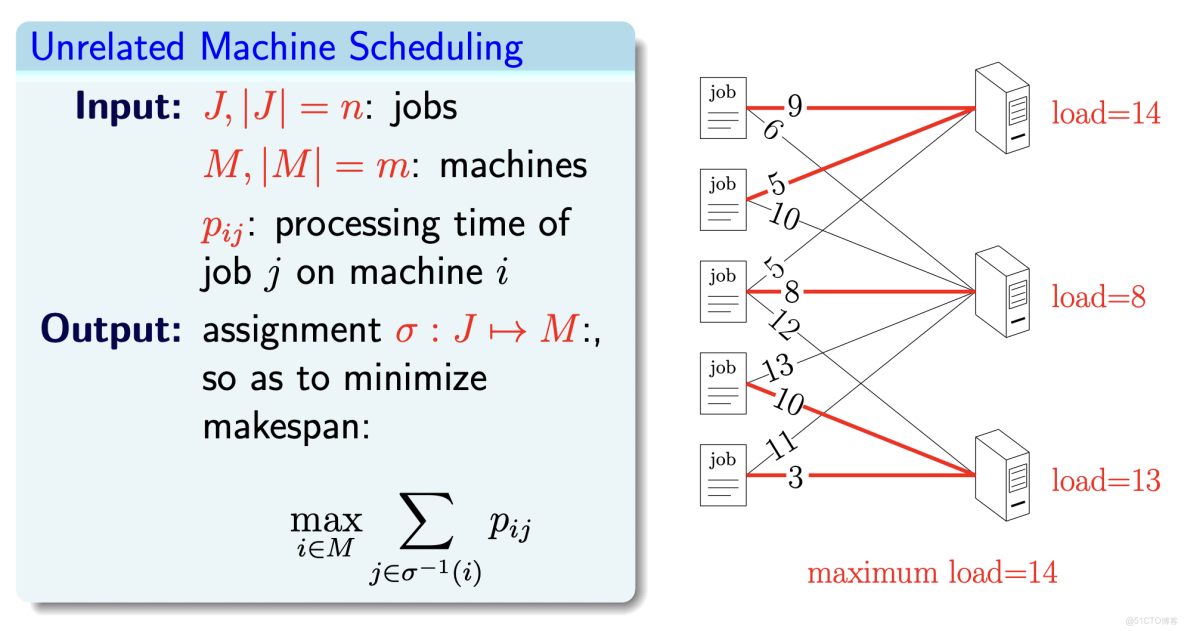
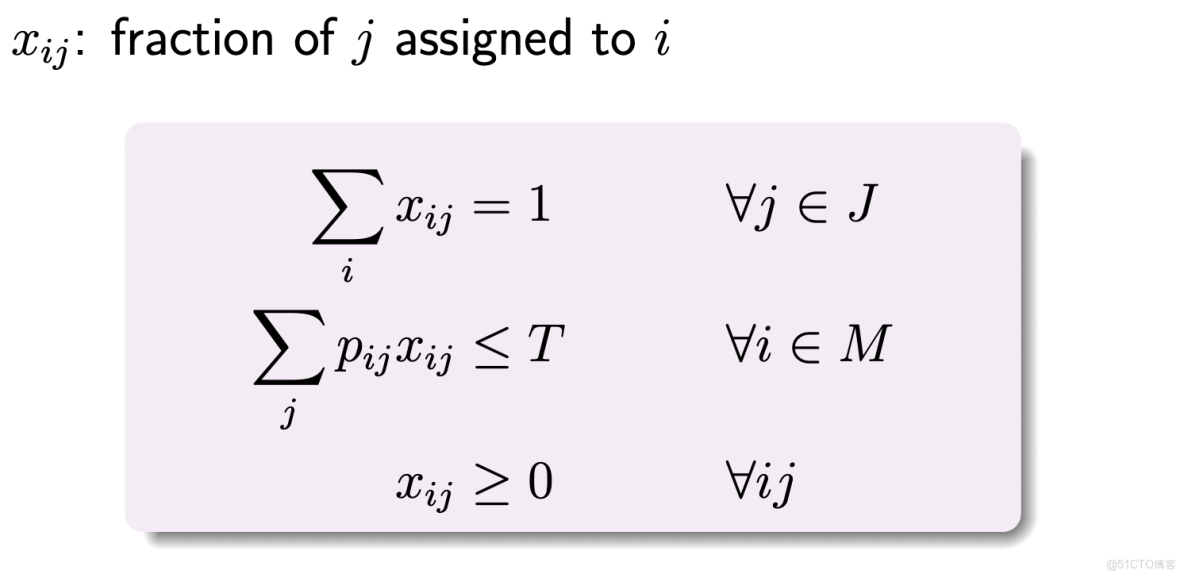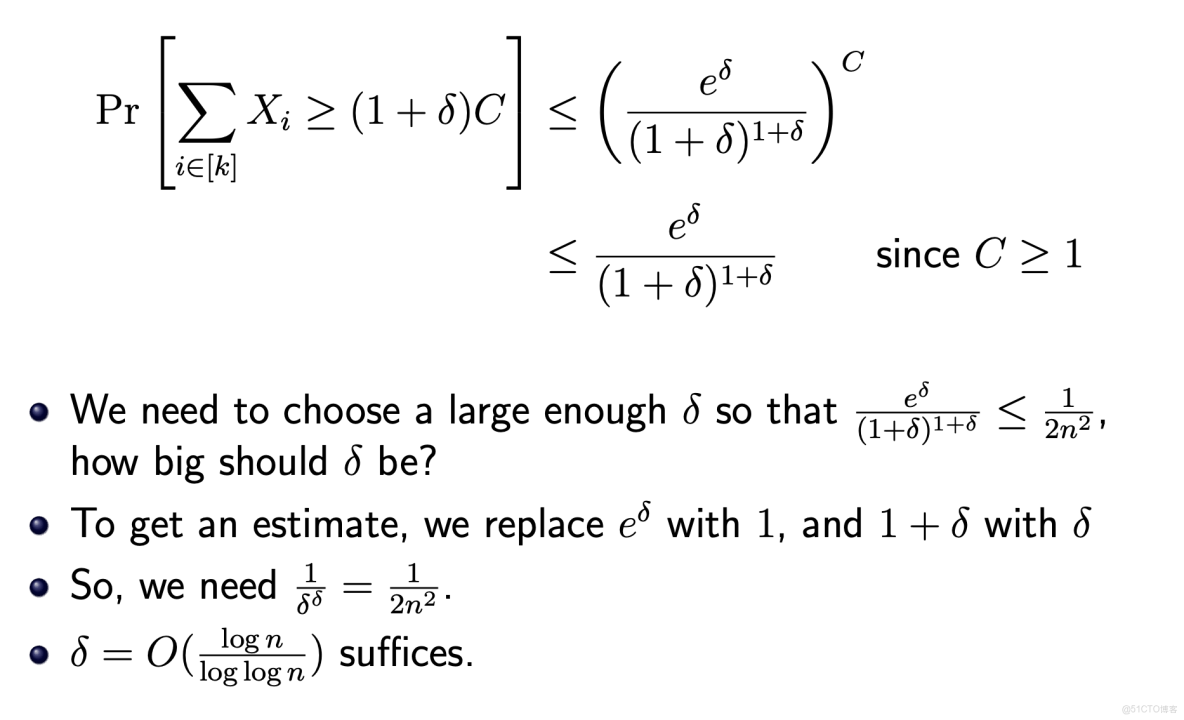Unrelated Machine Scheduling

轉化為判定形式，判定所有機器的 load 能否均不超過 T

一個問題是 integrality gap 可能會非常大，如 1 個任務，n 個機器，在每個機器時間上都是 1。整數最優解是分給任意一個機器，是 1。但 LP 會均分這個任務，最優解為 1/n。這樣 integrality gap 是 n。

為了解決這個問題，當 pij>T 時，令 xij 必須為 0，這樣就需要令 T 為二分的常數，不能為 LP 的變量。

fix 一個機器 i，將 xij>0 的任務 j 按照 pij 降序排列，分別建一個 sub-machine，令每個 sub-machine 承擔不超過 1 的 fraction（按照順序分配即可，只有每個機器的最後一個 sub-machine 擁有的 fraction 可能小於 1，其餘均為 1）。

之後這對應了二分圖匹配的 LP （即每個點 v 有一個 constraint 為 ∑uxuv≤1），直接進行一個二分圖匹配，讓每個任務都匹配一個 sub-machine。

這樣最壞的情況，就是對於一個 設施的每一個 sub-machine 都分到了連接到該設施的第一個任務（因為從大到小排序了）

就是湊一下係數可以發現近似比為 2。另外這個 2 也是 integrality gap，考慮 n+1 個任務分到 n 個機器，所有時間都是 1。這樣整數解必然有一個機器運行兩個任務，時間為 2。而 LP 可以讓每個機器運行 1+1/n 個任務。所以 integrality gap 為 2/(1+1/n)≈2。

Congestion Minimization

k 對源匯，每對需要 1 單位流量。最小化流量最大的邊的流量。

源點均為 s，匯點均為 t：令每條邊容量為 1，求 s 到 t 的最大流 L，答案為 ⌈k/L⌉。
源點均為 s，匯點不同：二分，判定 c 是否可行。建立超級匯點，每個匯點向超級匯連容量為 1 的邊。每條邊容量為 c，從 s 出發 k 的流量，cehck 是否都能到超級匯。
源匯均不同的話無法用上面的做法，因為這樣會丟失點對關係，無法保證從 si 出發的流量到達 ti。

C 表示最大擁塞，有一個 typo，左邊的 LP 的第二個限制應為對所有 e 均有 ∑i,P∈Pi,e∈PxP≤C。

左邊是一個指數級變量個的 LP，si 到 ti 之間的每條路徑 P 之間有一個變量 xP，表示這個路徑的 fraction。右邊的 LP 和左邊等價，就是將路徑的 fraction 放到了每條邊上，可以通過逐漸求增廣路的方式轉化為左邊的 LP。

具體算法為：

根據上面的算法，一條邊的期望擁塞為 ∑i,P∈Pi,e∈PxP 是不超過 C 的。

用 chernoff bound，限制每條邊的擁塞超過 (1+δ)C 的概率不超過 12n2 這樣通過 union bound 可以 w.h.p 保證 ratio 為 δ。

因為這裏令 δ→∞ ，所以 chernoff bound 中的界 eδ(1+δ)1+δ≈eδδδ=O(1δδ)。