快速排序VS大根堆排序:從原理到實戰(附大根堆完整代碼+實例拆解)
剛做排序實驗時,我一直搞不懂:明明快速排序平均速度更快,為啥有時候還要用大根堆排序?後來才發現,快速排序在最壞情況會退化到O(n²),而大根堆排序不管輸入啥,始終穩定在O(nlogn)——這倆的選擇,本質是“速度優先”和“穩定優先”的權衡。
今天從兩種排序的核心原理講起,對比它們的時間複雜度,重點拆解大根堆排序的建堆、交換、調整步驟(用實例[4,6,8,5,9]一步步走),最後給完整可運行代碼,幫你搞懂什麼時候用哪種排序。
一、先搞懂:兩種排序的核心邏輯
1. 快速排序:“分而治之”選基準
把數組分成兩部分,選一個“基準”(比如數組最後一個元素),讓左邊都比基準小,右邊都比基準大,再遞歸處理左右兩部分。就像整理書架,先選一本書當參照,把比它薄的放左邊,厚的放右邊,再分別整理左右兩堆。
2. 大根堆排序:“堆頂最大”逐個拎出
先把數組建成“大根堆”(完全二叉樹,每個父節點都比孩子大),此時堆頂是最大元素;把堆頂和最後一個元素交換(最大元素放最後),再調整剩下的元素重新成大根堆,重複直到所有元素有序。像從一堆蘋果裏每次挑最大的放最後,挑完剩下的再挑最大的。
二、關鍵對比:時間複雜度+適用場景(表格更清晰)
兩種排序的核心差異在穩定性和時間複雜度,直接用表格對比,新手也能看懂:
|
對比維度
|
快速排序
|
大根堆排序
|
|
核心思想
|
分治+基準劃分
|
大根堆構建+堆頂交換+堆調整
|
|
最壞時間複雜度
|
O(n²)(數組已有序/逆序,基準選得差)
|
O(nlogn)(任何輸入都穩定)
|
|
最好時間複雜度
|
O(nlogn)(基準能均分數組)
|
O(nlogn)(無差別,輸入不影響)
|
|
平均時間複雜度
|
O(nlogn)
|
O(nlogn)
|
|
空間複雜度
|
O(logn)(遞歸棧)/ O(1)(原地版)
|
O(1)(原地排序,不用額外空間)
|
|
適用場景
|
數據無序、追求平均速度(如日常數據排序)
|
數據可能有序、需要穩定性能(如系統排序)
|
|
缺點
|
最壞情況性能差,不穩定
|
常數項大,平均速度比快排慢
|
三、重點拆解:大根堆排序的3個核心步驟(實例+圖解)
大根堆排序的關鍵是“建堆”和“堆調整”,用實驗實例arr=[4,6,8,5,9]一步步拆解,保證你看會:
1. 步驟1:理解“大根堆”的結構
大根堆是完全二叉樹,滿足兩個條件:
- 每個父節點的值 ≥ 左右孩子的值;
- 數組存儲時,若父節點下標為
i,左孩子是2i+1,右孩子是2i+2(從0開始計數)。
實例初始數組[4,6,8,5,9]對應的完全二叉樹:
4(i=0)
/ \
6(i=1) 8(i=2)
/ \
5(i=3)9(i=4)顯然不符合大根堆(4<6、4<8、6<9),需要先“建堆”。
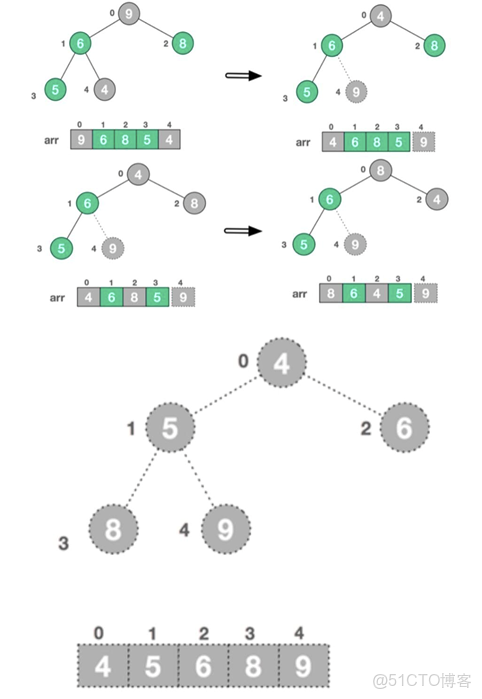
2. 步驟2:建堆(從最後一個非葉子節點開始)
建堆不是從根開始,而是從最後一個非葉子節點(下標=數組長度//2 -1,實例中是i=1,值為6)往前調整:
- 處理i=1(值6):右孩子9>6,交換6和9 → 此時子樹變成
[9,5],符合大根堆; - 處理i=0(值4):左孩子9>4、右孩子8>4,選最大的左孩子9交換 → 數組變成
[9,5,8,4,6];
交換後i=0的子樹[5,4,6]不符合,繼續調整5:右孩子6>5,交換5和6 → 最終大根堆數組[9,6,8,4,5],對應樹:
9(i=0)
/ \
6(i=1) 8(i=2)
/ \
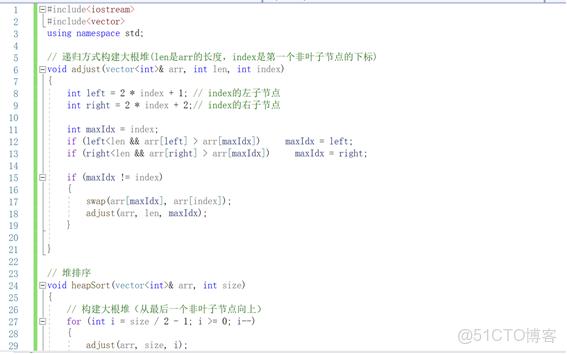
4(i=3)5(i=4)3. 步驟3:交換+調整堆(逐個提取最大值)
建堆後,堆頂是最大元素,每次把堆頂和“未排序部分的最後一個元素”交換,再調整堆:
- 第一次交換:堆頂9和最後一個元素5交換 → 數組
[5,6,8,4,9](9已排好);
調整前半部分[5,6,8,4]:5<6、5<8,交換5和8 → 數組[8,6,5,4],堆恢復; - 第二次交換:堆頂8和最後一個元素4交換 → 數組
[4,6,5,8,9](8已排好);
調整前半部分[4,6,5]:4<6,交換4和6 → 數組[6,4,5],堆恢復; - 第三次交換:堆頂6和最後一個元素5交換 → 數組
[5,4,6,8,9](6已排好);
調整前半部分[5,4]:5>4,無需調整; - 第四次交換:堆頂5和最後一個元素4交換 → 數組
[4,5,6,8,9](5已排好);
只剩一個元素4,排序結束。
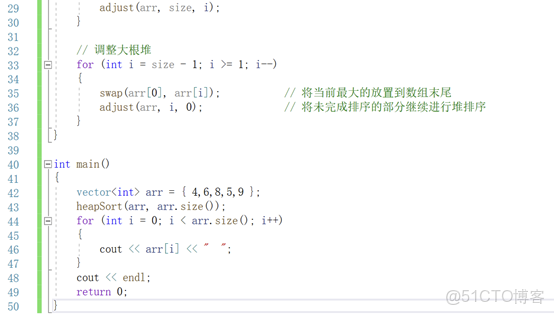
四、大根堆排序完整可運行代碼
#include <stdio.h>
#include <vector>
#include <iostream>
using namespace std;
// 調整大根堆:讓以i為根的子樹符合大根堆規則(核心函數)
void adjustHeap(vector<int>& arr, int size, int i) {
int maxIdx = i; // 初始化最大值下標為根
int left = 2 * i + 1; // 左孩子下標
int right = 2 * i + 2; // 右孩子下標
// 若左孩子比根大,更新最大值下標
if (left < size && arr[left] > arr[maxIdx]) {
maxIdx = left;
}
// 若右孩子比最大值大,更新最大值下標
if (right < size && arr[right] > arr[maxIdx]) {
maxIdx = right;
}
// 若最大值不是根,交換並遞歸調整子樹
if (maxIdx != i) {
swap(arr[i], arr[maxIdx]);
adjustHeap(arr, size, maxIdx); // 調整交換後的子樹
}
}
// 大根堆排序主函數
void heapSort(vector<int>& arr) {
int n = arr.size();
// 1. 構建大根堆:從最後一個非葉子節點開始往前調整
for (int i = n / 2 - 1; i >= 0; i--) {
adjustHeap(arr, n, i);
}
// 2. 逐個提取最大值:交換堆頂和末尾元素,調整堆
for (int i = n - 1; i >= 1; i--) {
swap(arr[0], arr[i]); // 堆頂(最大)和末尾交換,最大元素歸位
adjustHeap(arr, i, 0); // 調整剩餘i個元素為大根堆
}
}
// 快速排序輔助函數:劃分區間(按基準劃分左右)
int partition(vector<int>& arr, int first, int end) {
int pivot = arr[end]; // 選末尾元素為基準
int i = first - 1; // i是小於基準區間的右邊界
for (int j = first; j < end; j++) {
// 若當前元素小於等於基準,加入左區間
if (arr[j] <= pivot) {
i++;
swap(arr[i], arr[j]);
}
}
// 基準放到左區間末尾,此時左<基準<右
swap(arr[i + 1], arr[end]);
return i + 1; // 返回基準下標
}
// 快速排序主函數
void quickSort(vector<int>& arr, int first, int end) {
if (first < end) {
int pivotIdx = partition(arr, first, end); // 劃分區間
quickSort(arr, first, pivotIdx - 1); // 遞歸左區間
quickSort(arr, pivotIdx + 1, end); // 遞歸右區間
}
}
// 測試函數
int main() {
// 實驗用例
vector<int> arrHeap = {4, 6, 8, 5, 9};
vector<int> arrQuick = arrHeap; // 複製數組用於快速排序對比
// 大根堆排序
cout << "大根堆排序前:";
for (int num : arrHeap) cout << num << " ";
heapSort(arrHeap);
cout << "\n大根堆排序後:";
for (int num : arrHeap) cout << num << " ";
// 快速排序
cout << "\n\n快速排序前:";
for (int num : arrQuick) cout << num << " ";
quickSort(arrQuick, 0, arrQuick.size() - 1);
cout << "\n快速排序後:";
for (int num : arrQuick) cout << num << " ";
return 0;
}
運行結果(和實驗一致)
大根堆排序前:4 6 8 5 9
大根堆排序後:4 5 6 8 9
快速排序前:4 6 8 5 9
快速排序後:4 5 6 8 9五、避坑點(實驗中容易錯的地方)
- 大根堆建堆方向錯:很多人從根開始建堆,其實要從最後一個非葉子節點(n/2-1)往前,因為葉子節點本身就是合法的堆;
- 快速排序基準選得差:若選第一個/最後一個元素當基準,數組有序時會退化到O(n²),實際可選“三數取中”(首、中、尾選中間值);
- 堆調整漏遞歸:交換根和最大值後,子樹可能不符合規則,必須遞歸調整子樹,否則堆會錯亂;
- 數組越界:調整堆時,要判斷
left < size和right < size,避免訪問不存在的孩子節點。
六、總結:什麼時候用哪種排序?
- 選快速排序:數據無序、追求平均速度(如App中的列表排序、日常數據處理),缺點是最壞情況不穩定;
- 選大根堆排序:數據可能有序、需要穩定性能(如系統任務調度、海量數據排序),缺點是常數項大,平均速度比快排慢。