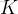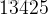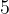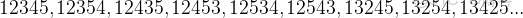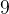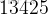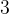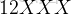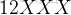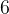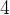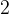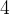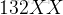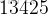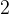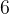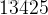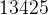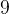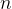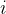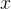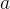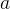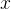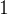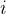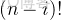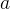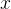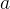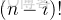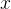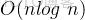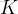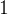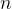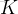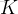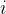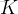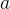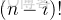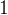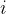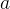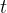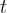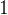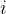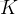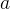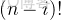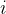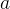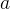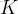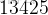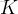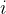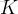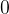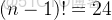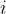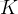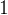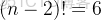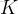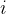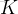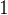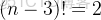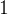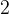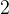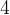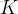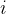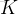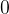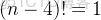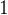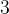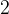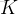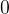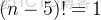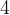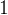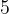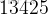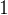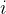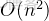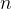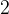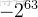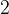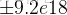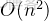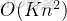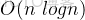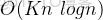#include<bits/stdc++.h>
using namespace std;

typedef long long LL;
const int N = 1e6 + 10;
const LL P = 998244353;

int n, a[N];
LL c[N], fac[N];

void add(int x, LL d) {
	for (; x <= n; x += x & -x) {
		c[x] = (c[x] + d) % P;
	}
}

LL get_sum(int x) {
	LL res = 0;
	for (; x >= 1; x -= x & -x) {
		res = (res + c[x]) % P;
	}
	return res;
}

int main () {
	ios::sync_with_stdio(false);
	cin.tie(0);
	
	cin >> n;
	for (int i = 1; i <= n; i ++) {
		cin >> a[i];
	}
	
	memset(c, 0, sizeof(c));
	fac[0] = 1;
	for (int i = 1; i <= n; i ++) {  // 初始化階乘數組 
		fac[i] = fac[i - 1] * i % P;   // 一定要取模！！ 
	}
	
	LL ans = 0;
	for (int i = 1; i <= n; i ++) {
		int x = a[i];
		LL t = ( (x - 1) - get_sum(x - 1) + P) % P;   
		// get_sum 求出來的是出現過比 x 小的數，要求沒出現過的 
		ans = (ans + t * fac[n - i] % P) % P;
		add(x, 1);   // 把 x 放進去 
	}
	cout << (ans + 1) << "\n";   // 別忘了加 1，ans 是在題目給出排列前面的排列數 
	
	return 0;
}

#include<bits/stdc++.h>
using namespace std;

typedef long long LL;
const int N = 22;

int n, a[N];
LL c[N], fac[N];

void add(int x, LL d) {
	for (; x <= n; x += x & -x) {
		c[x] += d;
	}
}

LL get_sum(int x) {
	LL res = 0;
	for (; x >= 1; x -= x & -x) {
		res += c[x];
	}
	return res;
}

int main () {
	ios::sync_with_stdio(false);
	cin.tie(0);
	
	int K;
	cin >> n >> K;
	
	fac[0] = 1;
	for (int i = 1; i <= n; i ++) {
		fac[i] = fac[i - 1] * i;   // 階乘這一塊 /. 
	}
	
	while (K --) {
		char s[5];
		cin >> s;
		
		if (s[0] == 'Q') {   // 正展開 
			memset(c, 0, sizeof(c));   // 每個詢問都要清空一次 
			LL ans = 0;
			
			for (int i = 1; i <= n; i ++) {
				cin >> a[i];
				LL t = a[i] - 1 - get_sum(a[i] - 1);
				ans += t * fac[n - i]; 
				add(a[i], 1);
			}
			
			cout << (ans + 1) << "\n";
		}
		
		else {   		   // 逆展開 
			LL k;     // 這玩意可有 20! 那麼大 
			cin >> k; k --;   // 減減 
			set<int> set_;  // 未使用數字集合 
			for (int i = 1; i <= n; i ++) {
				set_.insert(i);    // 全都放進去 
			}
			
			for (int i = 1; i <= n; i ++) {
				int aa = k / fac[n - i];  // 重名了用 aa
				auto it = set_.begin(); 
				advance(it, aa);   // 移到第 aa + 1 個元素 
				a[i] = *it;
				set_.erase(*it);     // 刪了 
				k -= aa * fac[n - i];  // 別忘了減 
			}
			
			for (int i = 1; i <= n; i ++) {
				cout << a[i] << " ";
			}
			cout << "\n";
 		}
	}
	
	return 0;
}

#include<bits/stdc++.h>
using namespace std;

typedef long long LL;
const int N = 22;

int n, a[N];
LL c[N], fac[N];

void add(int x, LL d) {
	for (; x <= n; x += x & -x) {
		c[x] += d;
	}
}

LL get_sum(int x) {
	LL res = 0;
	for (; x >= 1; x -= x & -x) {
		res += c[x];
	}
	return res;
}

// 在樹狀數組 c 中找第 k 小的可用數（k 從 1 開始）
// 這裏利用了樹狀數組的特性，即查詢 1 到 n 最多遍歷 log n 個值 
int kth(int k) {
    int p = 0, s = 0;    
	// p 是當前樹狀數組上剛剛遍歷到的節點（當前遍歷範圍可使用數字最大值） 
	// s 是當前已遍歷範圍裏可使用數字的總個數 
	// 整個過程就是不斷調整 p 的大小（遍歷範圍的最大值）
	// 來看看 s 什麼時候剛好等於 k - 1
	// 由於最後 s 肯定停在 k - 1 的臨界值（再大一點就不是了）
	// 所以 p + 1 是第 k 個數 
	 
    // n <= 20，所以 1 << 5 = 32 足夠
    for (int i = 5; i >= 0; i --) {
        int t = p + (1 << i);
        if (t <= n && s + c[t] < k) {  // 節點還小於 n，總個數要小於 k 
            s += c[t];
            p = t;
        }
    }
    
    // 現在 p 是最大的滿足 get_sum(p) < k 的下標 
    return p + 1;
}

int main () {
	ios::sync_with_stdio(false);
	cin.tie(0);
	
	int K;
	cin >> n >> K;
	
	fac[0] = 1;
	for (int i = 1; i <= n; i ++) {
		fac[i] = fac[i - 1] * i;   // 階乘這一塊 /. 
	}
	
	while (K --) {
		char s[5];
		cin >> s;
		
		if (s[0] == 'Q') {   // 正展開 
			memset(c, 0, sizeof(c));   // 每個詢問都要清空一次 
			LL ans = 0;
			
			for (int i = 1; i <= n; i ++) {
				cin >> a[i];
				LL t = a[i] - 1 - get_sum(a[i] - 1);
				ans += t * fac[n - i]; 
				add(a[i], 1);
			}
			
			cout << (ans + 1) << "\n";
		}
		
		else {   		   // 逆展開 
			LL k;     // 這玩意可有 20! 那麼大 
			cin >> k; k --;   // 減減 
			
			memset(c, 0, sizeof(c));   // 現在這個樹狀數組是存未使用的數字 
			for (int i = 1; i <= n; i++) {
				add(i, 1);     // 全都放進去 
			}
			
			for (int i = 1; i <= n; i ++) {
				int aa = k / fac[n - i];   // 重名了用 aa
				int t = kth(aa + 1);     // 第 (aa + 1) 小，kth 是 1-indexed
				a[i] = t;
				add(t, -1);              // 刪掉這個數
				k -= aa * fac[n - i];      // 別忘了減 
			}
			
			for (int i = 1; i <= n; i ++) {
				cout << a[i] << " ";
			}
			cout << "\n";
 		}
	}
	
	return 0;
}