一.寫在前面

　　本節主要講的是上一節學習圖中的按目標分類的橙色方塊中的regression，即所要解決的問題的解為數值。本節由一個案例貫穿，即預測神奇寶貝進化後的戰鬥力，挺有趣的一個案例。本節略長，請耐心看，相信會有收穫的，做我們這行的最重要的就是要有耐心。

二.案例説明

　　所要研究的案例是想要預測神奇寶貝進化後的戰鬥力用cp值表示，具體案例描述如下圖2-1。

　　　　　　　　　　　　　　　　　　　　　　　 圖2-1 案例描述

圖中有幾個變量這裏做個介紹x_cp為未進化前的戰鬥力值，x_hp為該物種的生命值，x_w為該物種的體重，x_h為該物種的身高，而我們所要做的就是尋找到這樣一個函數f，它以這些變量作為輸入，輸出進化後的戰鬥力y。

三.從機器學習角度來研究該案例

　　在上一節中曾提到過機器學習的三個步驟即機器學習的框架，接下來就按照者三個步驟來分析這個案例。

3.1 定義函數池

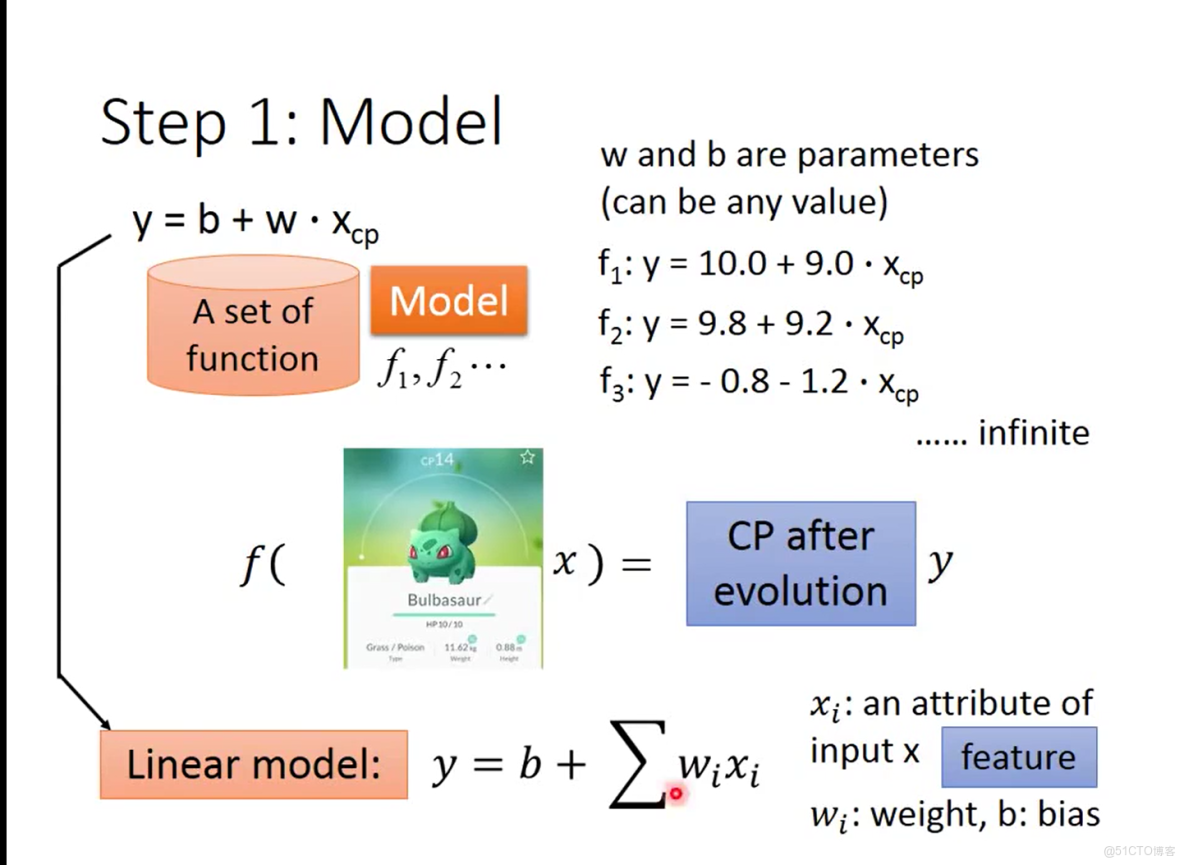
首先我們需要定義一個函數池即需要定義模型，還記的學習圖中藍色模塊的含義嗎？在這裏就是決定你所定義的模型是屬於什麼類型的，可以是線性的linear model 也可以是非線性的non-linear model ,這裏為便於講解先假設為線性模型,並且暫時僅考慮x_cp這一個變量,假設的模型如圖3-1

 　　　　　　　　　　　　　　　　　　　　　　　　圖3-1 假設的初始模型

從圖3-1中可以看到假設的模型為y=b+w*x_cp，其中w稱為x_cp這個變量所佔的權重，b為偏移量，按照這個模型可以隨機初始化w和b的值獲得不限數量的函數f，當將其他生命值、體重的變量也考慮在內，就得到圖中右下角的模型，這裏公式不太好編寫，就寫成拆開的形式y = b+w₁*x_cp+w₂*x_w+w₃*x_h+...w_i*x_i

3.2 對各個函數評價

在完成了函數池的定義之後，就需要一種機制來評價各個函數的好壞，這裏就有兩個角度了，你可以評價一個函數有多好你也可以評價一個函數有多差，本案例中使用的是loss function 即損失函數L用於評價一個函數有多差，其值越大表示一個函數越差。損失函數L是將函數池中的函數作為輸入，它的定義可以有很多種，在這個案例使用的損失函數如圖3-2

　　　　　　　　　　　　　　　　　　　　　　　 圖3-2 損失函數

圖中的損失函數就是用訓練數據中神奇寶貝進化後的真實值減去函數池中選出的一個函數進行預測得到的預測值，再對這些值平方後進行累加。這裏額外將講一下損失函數的定義完全是可以由你自己決定的，會受到具體所要研究的問題的影響。

3.3 選出最優的函數

3.3.1 使用梯度下降的方式

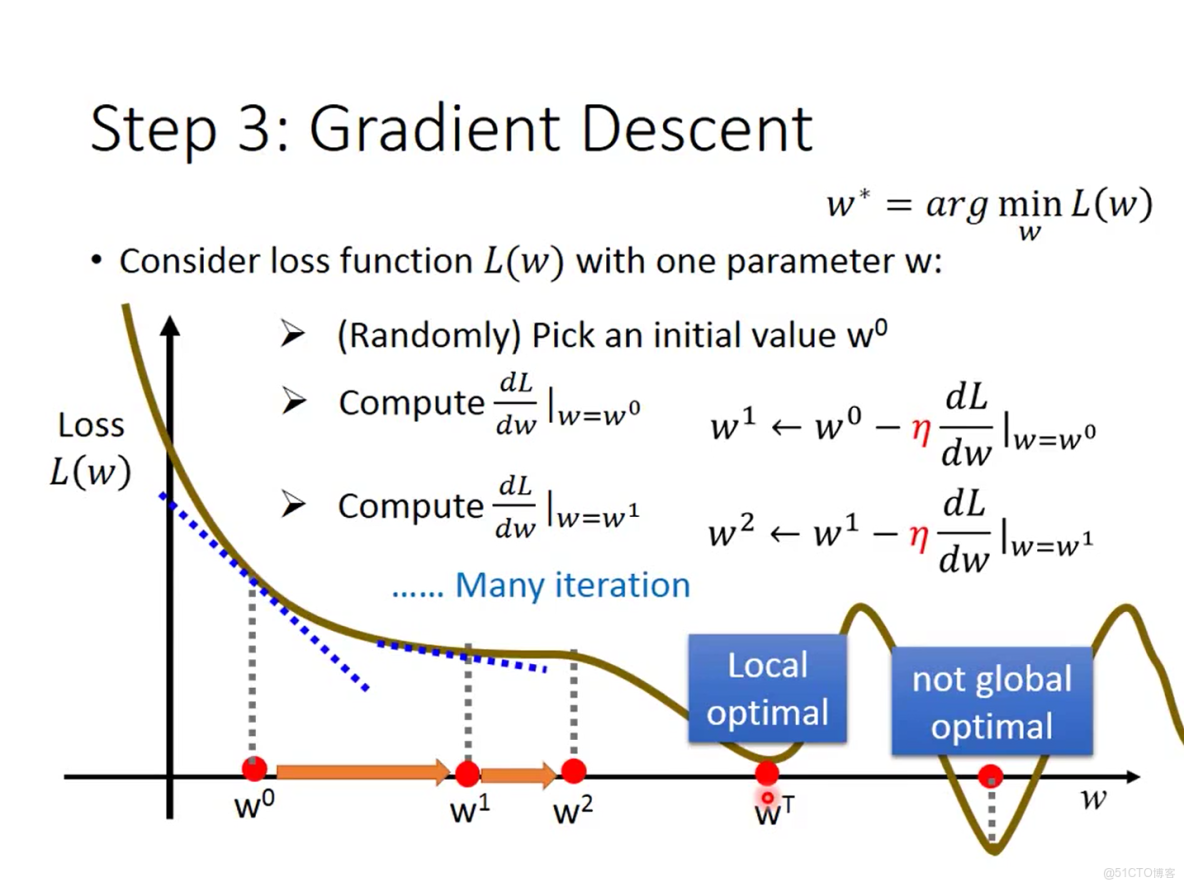
通過初始化各變量對應的權重參數w_i和偏移量b可以得到大量的函數，如何根據損失函數選出最優的函數，所謂的最優函數就是使損失函數達到最小，而損失函數的輸入是函數池中的函數，函數池中的函數的變量是w_i(i=1,2,3,4....)和b,也就是説損失函數也是w_i和b的函數，那麼問題就轉變為確定w_i(i=1,2,3,4....),b的值使損失函數的值達到最小。在這裏使用梯度下降的方法來求這個w_i和b，梯度下降的概念十分重要，這裏只做初步的講解，不是本節的重點之後會重點提到，簡單來説梯度下降的思想類似於下山，當你處於山上的某一處時你想要下山，你可以這麼做沿着當前所在位置尋找一條最為陡峭的向下的方向，沿着這個方向邁出一步，然後在新的起點不斷重複這個過程。具體的舉個例子，為了舉例方便，簡化了損失函數L,假設L僅與一個變量w相關,即L(f) = L(w)，例子如圖3-3

　　　　　　 

　　　　　　　　　　　　　　　　　　　　　　　圖3-3梯度下降

先對圖中所描述的過程進行一個講解，首先我們要求的是使損失函數L達到最小時的w的值，先隨機初始一個w的值w₀,然後找出該點的梯度，然後根據梯度值的正負決定本次調整的方向，圖中例子w₀處的梯度為負值，這表明在w₀的右側領域函數的值是下降的，所以下一個點調整的方向為向右側方向，這就像之前提到的下山，先確定出下山的方向，當確定完下山的方向後，便要邁出腳步下山，而這一步要邁多大，即對w₀調整該有多大這受到兩個因素的影響，一個是w₀出的梯度值，還有一個就是被稱為學習率的值就是圖中紅色的字母n,具體的公式圖中已經給出，可以按照圖中的公式不斷進行梯度下降得到w₁,w₂....,但當到達點w_t時發現該點的梯度值為0，則無法再繼續進行梯度下降，梯度下降過程結束機器將w_t認為是最優點，但我們通過觀察圖形可以發現w_t並不是全局最優點只是局部最優點，這個現象稱為陷入局部最優，至於解決的方法在之後的章節將提到。以上所講的假設是單個變量的情形，多變量的情形與之類似，不同之處在於梯度的計算在單變量時是對變量求導而在多變量時則是對各個變量求偏導，用得到的偏導值來更新對應的變量

3.3.2 過擬合現象

　我們完成上述步驟後就可以得到函數池中最好的一個函數，在這個案例中不僅使用了簡單的線性函來預測，為了儘可能更好的擬合訓練數據集中的數據，訓練數據集中的數據如圖3-4 為10只神奇寶貝進化前後的cp值，還同時考慮二次，三次，四次，五次多項式的情況。

 　　　　　　　　　　　　　　　　　　　　　　　圖3-4 訓練集中的數據

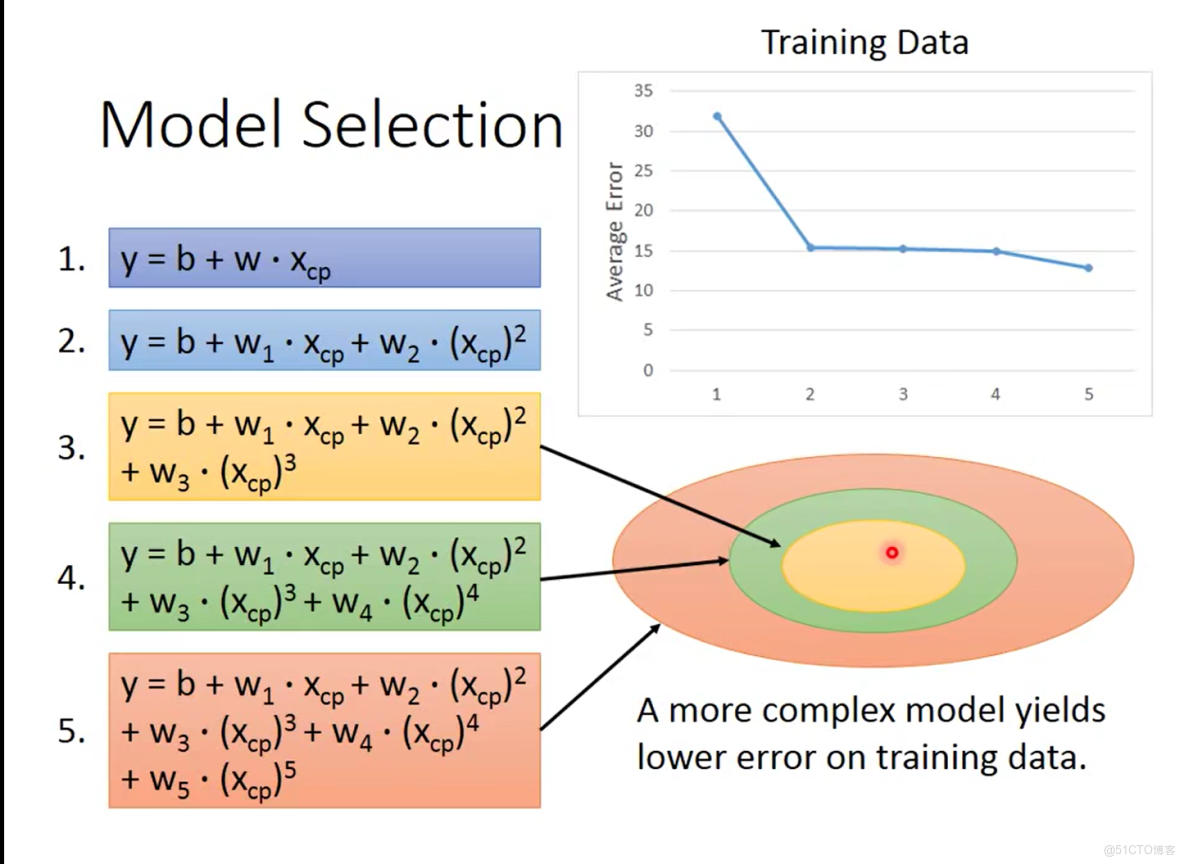
通過上文介紹的方法，為各個多次式對應的函數池選出最優的函數，這個的意思就是説為從帶有二次項的函數池中選出最優的函數，再從帶有三次項的函數池中選出最優的函數等等依此下去直到帶有五次項的函數池結束，各次項對應的最優函數在訓練數據集上的表現如圖3-5

 

 　　　　　　　　　　　　　　　　　　　　　圖3-5 各模型在訓練集上的表現情況

從圖3-4可以看出五次項的函數在訓練集上產生的平均誤差最小，產生這種的原因是因為帶有更高次項的函數更為複雜，表達能力更強同時其本身也包含了低次項的函數所能保持的範圍。可以看到五次項的最優函數在訓練集上取得了最好的效果，但是否就意味着這個函數就是我們所要尋找的最優的函數，顯然不是的還需要經過測試集上的效果驗證，所謂的測試集是指一批全新的數據這些數據並沒有在訓練集中出現過，五個最優函數在測試集上表現如圖3-6。

 　　　　　　　　　　　　　　　　　　　圖3-6 過擬合現象

從圖3-5可以發現在訓練集上有着優秀表現的4次項最優函數和5次項最優函數，在測試集上表現的很差，這種現象就被稱為過擬合，即在訓練集上有着優秀表現的模型在測試集上表現的很差，造成這一現象的主要原因在於訓練集中的數據量太少而4次項和5次項的函數的表達能力足夠強，導致訓練集中的所有數據均被模型給記住了，導致機器並不是學習到了什麼，更像是將所有的數據給背了下來。舉個身邊類似的例子，就像你去考駕照時，多次重複在駕校聯繫科目裏的項目，會使你產生一些奇怪的技巧，比方説在側方停車時，你會記得當後視鏡看到輪胎內側時回方向盤，這些技巧會讓你在駕考中取得高分，但這並不代表你能在實際道路能開的好車。

3.4 進一步優化

為了得到更好的擬合效果，包括訓練和測試集上的，可以對前面的步驟進行優化，優化主要為兩個方面，這兩個方面分別體現在機器學習的三大步中的前兩步，對第一步的優化，我們可以重新考慮函數池，前面的函數池的設計的前提時均只考慮神奇寶貝未進化前戰鬥力x_cp這一各變量，其實還受其他很多因素的影響包括不同神奇寶貝的物種、神奇寶貝的體重、神奇寶貝的身高等等，將這些變量均考慮在內重新設計函數池，這裏不再贅述由興趣的可以去看李弘毅老師的視頻，這裏重點講一下優化的第二步，是對損失函數的優化，優化後的函數如圖3-6。

 　　　　　　　　　　　　　　　　　　　　圖3-7 正則化　　　　　　　　　　　　　　　　　　　

可以看到優化後的損失函數就是在原先的基礎上增加了與輸入變量由關的項，到這不經為考慮為什麼要添加這麼一項，不如反過來思考，添加了這一項之後損失函數會如何，還記得前面我所講的我們所要尋找的就是使損失函數最小時的各變量取值，那麼也就意味着相比於原先未優化前就是希望各變量也就是w_i的值儘可能的小，w_i的值儘可能的小將更受到青睞，那為什麼希望由更小的w_i的值，這都是希望為了獲得時我們最總獲得的預測函數更加的平滑，這裏的平滑是如何體現的具體看圖中的紅字部分，當w_i儘可能小時，x_i引起的變化對最終預測值的影響也將變小，這就做到了降噪的效果，可以使最終的函數適應性更強，也就説當x_i出現較大幅度的震盪，這種震盪將會一定程度的被削弱。

 

四.寫在最後，兩個疑問

在視頻最後有提出兩個疑問，第一個疑問老師給出瞭解答，我這也順便記錄一下是一個很好的問題，問題使來自於進一步優化的第二步，在損失函數後面新添加的項重為什麼不考慮b，即偏移量，實話實説這個問題問出來我也楞了一下，確實沒有考慮過，該好好反思一下，這個問題的答案是因為b不會影響函數的平滑程度而是影響曲線的上下偏移量。第二個問題老師在視頻沒有給出原因只給出答案，問題是如果它將優化後的得到的最終預測函數放到網絡上給大家使用，想説得到的平均誤差量會不會比在我們在優化過後再測試數據集上跑的效果好，答案是不會，不會的原因個人認為是這樣的其實回過頭來看整個介紹案例的過程，其實測試集的數據已經發生了泄露，我們人為的看到模型在測試集上的效果並不好而去做出一些調整其實這個過程測試數據就已經泄露了。最後寫這文章挺不容易的，希望有看的同學能有耐心的看完並指正出錯誤，大家多交流才能共同進步！