目錄

1.前言:

2.算法思路

2.1題目介紹

2.2思路優化

2.3分析情況

2.4 a + b > c 的情況

2.5 a + b < c 的情況

2.6總的解決步驟:

3.總結

1.前言:

各位友友們,大家好呀!!! 今天為大家帶來力扣上有效三角形個數這道題目的講解,希望可以為和我一樣陷入困惑的友友們帶來幫助呀.

題目來源:611. 有效三角形的個數 - 力扣（LeetCode）

2.算法思路

2.1題目介紹

其中涉及到一個數學知識

三個數能否構成三角形的有效條件是什麼?

任意兩邊之和大於第三邊(等價於任意兩邊之差小於第三邊)

兩個條件中,我們只需要使用其中一個即可

2.2思路優化

即當有三條邊a,b,c的時候,這三條邊能構造三角形的有效條件是:

1. a + b > c
2. a + c > b
3. b + c > a

這種情況中,我們需要比較這三個條件,但是當我們將數組進行排序之後,數組就是有序的了,此時只需要比較一個條件即可 

例如只有a,b,c三個元素的有序數組:a < b < c

這時只需要判斷a + b > c 這個條件是否成立即可,如果這個條件成立,那麼這三個數就可以構成一個有效的三角形

另外兩個條件是必然成立的:

1. c + a > b,因為c > b
2. c + b > a,因為c > a

2.3分析情況

如果直接枚舉所有的三元組,不難免時間複雜度非常高,可以去到O(N^3)

解決方法:先固定一個最大的數,然後找出符合題意的二元組

步驟:

1. 將數組進行排序,直接使用庫方法sort()
2. 固定最大的那個數

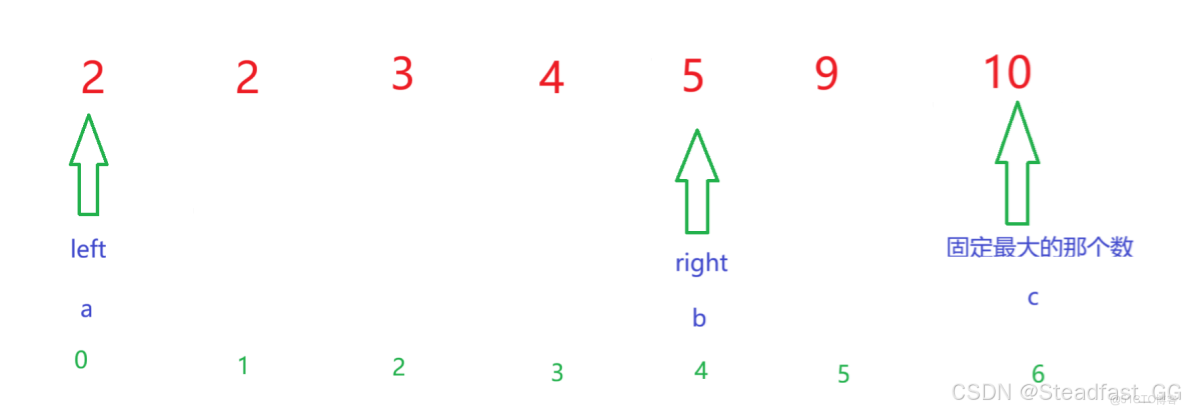
小編在這裏以下面的數組作為例子:

這裏使用的雙指針也就是left 和 right 兩個下標,其中left下標對應的數是 a ,right下標對應的數是 b.

此時a 和 b 的和 與 c 進行比較只有兩種情況:

1. a + b > c(構成三角形,另外兩個條件已經在數組有序前提下自動滿足了,無需再進行判斷)
2. a + b <= c(不構成三角形)

2.4 a + b > c 的情況

當前是a + b > c 的情況:

1.上面中,符合a + b > c 這個條件,這三個數可以構成有效三角形

2.在a 和 b 的中間還有其他一些數,這些數肯定是比 a 大的,也就是 在這個區間中的任意取值跟 b 進行組合之後必然滿足a + b > c 這個條件 ,另外其他兩個條件也肯定是滿足的,這樣的二元組一共有5 個,剛好是(right - left) 個,當枚舉完這些情況之後,right 下標的元素已經沒有價值了,此時right 向左移動

1. a + b > c
2. (比a大的數) + b > c

2.5 a + b < c 的情況

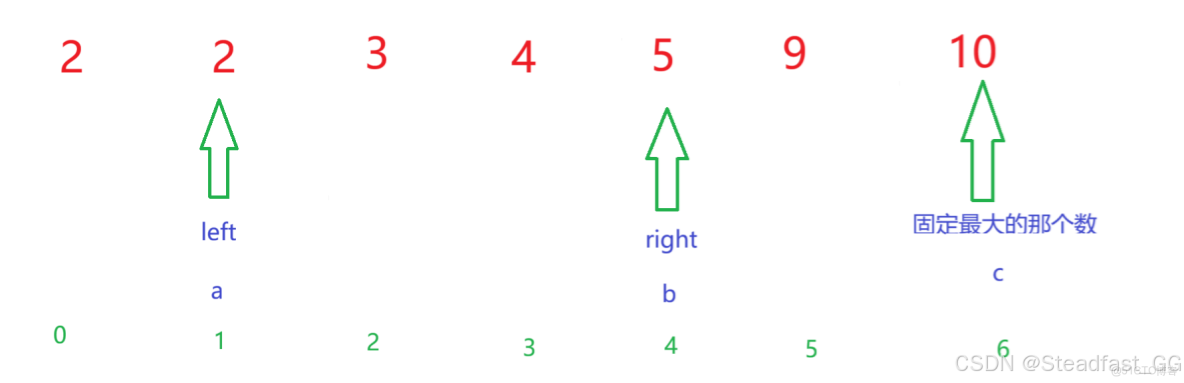
當right向左移動之後剛好是a + b < c 的情況:

此時a + b < c, 不能構成有效的三角形

小編在這裏的理解是:此時的a 太小,即使搭配最大的b也沒用,我們要是想讓 a 變大點,那麼就要讓left 向右移動

移動之後,還是要繼續判斷a + b 和 c 的 大小情況,然後left 和 right 分別作出相應的調整

通過前面的分析過程,我們可以總結出當已經固定好最大數之後,尋找二元組的兩種情況:

1. 當a + b > c 的時候,有(right - left) 種情況可以構成三角形,然後 right 向左移動(right --);
2. 當a + b <= c 的時候,此時不能構成三角形,a 太小,要讓a 變大,left就要向右移動(left ++);

2.6總的解決步驟:

所以這道題目總的解決步驟是:

1. 固定好最大的數,固定的數是會發生變化的,因為數組中的每一個數都有可能成為最長邊,引入循環來解決問題
2. 在固定好最大數的前提下,不斷尋找符合條件的二元組,也要引入循環來解決問題,另外left 和 right 在每次進行判斷之後都要作出相應的調整

1.固定最大的數:

for(int i = nums.length - 1 ; i >= 2; i --){
            
}

1. 在這裏面中,數組已經是有序的,最大的數在數組最後面,從最後面開始往前固定
2. i >= 2 作為 循環的終止條件,一旦 i < 2,也就沒有三個數了,我們要尋找的是三元組

2.尋找符合條件的二元組:

for(int i = nums.length - 1; i >= 2; i --){
            int left = 0;
            int right  =  i - 1;
            while(left < right){
                if(nums[left] + nums[right] > nums[i]){
                    count += right - left;
                    right --;
                }else{
                    left ++;
                }
            }
        }

在這裏面中,重要代碼的講解:

(1)

int left = 0;
            int right  =  i - 1;

每次固定完最大數尋找二元組之後,在新一輪固定中要將left 和 right 重新設置

(2)

while(left < right)

只要left 和 right 還沒相遇,我們就繼續尋找二元組,一旦left 和 right 相遇之後,也就是 left == right,這一輪尋找就結束,循環退出.這時可以開始固定下一個數繼續新一輪的尋找

(3)

count += right - left;

count 作為計數器 ,要使用前面的值再進行運算

經過前面的分析,這道題目已經沒有什麼難點了,小編給友友們附上完整的代碼:

class Solution {
    public int triangleNumber(int[] nums) {
        //定義計數器
        int count = 0;
        //1.先對數組進行排序,讓數組變成有序的
        Arrays.sort(nums);
        //2.固定最大的那個數
        for (int i = nums.length - 1; i >= 2; i--) {
            //
            int right = i - 1;
            int left = 0;
            //2.1利用雙指針法尋找二元組
            while (left < right) {
                //構成三角形的條件
                if (nums[left] + nums[right] > nums[i]) {
                    //這裏面中共有(right - left) 種情況符合題意
                    count += (right - left);
                    //此時right下標已經沒有價值了,right往左移動
                    right--;
                } else {
                    //不構成三角形的條件,此時a太小,讓 left 往右移動
                    left++;
                }
            }
            //while()循環退出之後,再更換固定的最長邊
        }
        return count;
    }
}