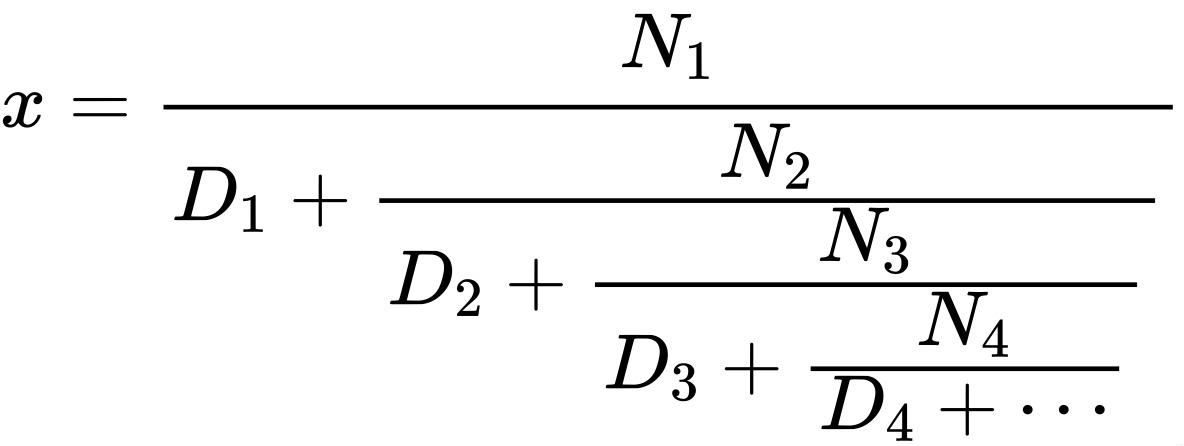本節的主要內容在於lambda函數和let函數,通過兩種新的函數形式減少了定義的使用,對過程設計進行了簡化。
lambda函數用於減少define的使用,使得過程的編制更加符合直覺,通過lambda(x)(fx)的形式可以減少很多函數體外的定義過程。
let函數更多用於定義局部變量,通過let體內的定義可以直接完成局部變量的運算,但需要注意區分let函數體內外的運算過程區分。
新函數與之前應用的函數無太大區別,屬於是之前函數的簡化,因此無太多練習。
補充了幾個算法,關於尋找方程根和函數不動點的內容。方程根值的尋找和之前的平方根求值思路是一致的,通過不斷縮小區間範圍,找到0點的對應的具體值。
不動點的概念如下,若x滿足方程f(x)=x且反覆的應用f:f(x)、f(f(x))、f(f(f(x)))…到最後其值無明顯變化時,可以認為找到了函數的不動點。
針對兩種函數的練習如下:
1.35 證明黃金分割率φ是變換1+1/x的不動點,並通過過程計算。
證明過程很簡單,根據黃金分割率φ的特性φ²=φ+1即可證明,計算過程如下:
點擊查看代碼
(define tolerance 0.0001)
(define (fixed-point f first-guess)
(define (close-enough? v1 v2)
(< (abs ( - v1 v2)) tolerance))
(define (try guess)
(let ((next (f guess)))
(if (close-enough? guess next)
next
(try next))))
(try first-guess))
(fixed-point (lambda (x) ( + 1.0 ( / 1.0 x))) 1.0)
1.61805555555555561.36 要求修改fixed-point過程,使其能夠打印出計算中產生的近似值序列。並找到log(1000)/log(x)的不動點。
前半個問題只需要在原有函數中添加newline和display函數即可解決:
點擊查看代碼
(define tolerance 0.0001)
(define (fixed-point f first-guess)
(define (close-enough? v1 v2)
(< (abs ( - v1 v2)) tolerance))
(define (try guess)
(newline)
(display guess)
(let ((next (f guess)))
(if (close-enough? guess next)
next
(try next))))
(try first-guess))後半個問題題目要求分別試驗用平均阻尼和不用平均阻尼時的計算步數(平均阻尼即將每次產出的新的guess進行二次變換,如取其和前一個guess的平均數) 不用平均阻尼時: 點擊查看代碼
> (fixed-point (lambda(x) ( / (log 1000) (log x))) 2.0)
2.0
9.965784284662087
3.004472209841214
6.279195757507157
3.759850702401539
5.215843784925895
4.182207192401397
4.8277650983445906
4.387593384662677
4.671250085763899
4.481403616895052
4.6053657460929
4.5230849678718865
4.577114682047341
4.541382480151454
4.564903245230833
4.549372679303342
4.559606491913287
4.552853875788271
4.557305529748263
4.554369064436181
4.556305311532999
4.555028263573554
4.555870396702851
4.555315001192079
4.5556812635433275
4.555439715736846
4.555599009998291
4.555493957531389
4.555563237292884使用平均阻尼時:
點擊查看代碼
(fixed-point (lambda(x)(average x ( / (log 1000) (log x)))) 2.0)
2.0
5.9828921423310435
4.922168721308343
4.628224318195455
4.568346513136242
4.5577305909237005
4.555909809045131
4.555599411610624
4.5555465521473675可見使用平均阻尼後減少了很多計算的步數,算法佔用空間和時間步數都有所節省。
1.37 要求解一個無窮連分式,
按照要求編寫過程,並根據題目要求代入n=1、d=1進行計算:
點擊查看代碼
(define (cont-frac n d k)
(define (try next k)
(let ((result ( / n (+ d next))))
(if (< k 1)
result
(try result (- k 1))
)
)
)
(try 0.0 k)
)
> (cont-frac 1.0 1.0 10)
0.6180555555555556
> (cont-frac 1.0 1.0 100)
0.61803398874989481.38 要求同上一題,不過這回需要借e-2的連分式,此處我編寫的程序結果持續振盪,我也在找原因,如有高手看出問題煩請提點,感謝!
點擊查看代碼
(define (3n+2? x)
( = (remainder (- x 2) 3) 0)
)
(define (mod3 x)
( / (- x 2) 3)
)
(define (cont-frac n d k)
(define (try next k)
(cond ((3n+2? k)
(let((result (/ n (+ (* (+ (mod3 k) 1) 2) next))))
(if (= k 1)
result
(try result (- k 1))
)
))
(else
(let((result (/ n (+ d next))))
(if (= k 1)
result
(try result (- k 1))
)
))))
(try 0.0 k)
)1.39 對正切函數的連分式定義過程
沒啥好説的,和前面一樣。
點擊查看代碼
(define (square x) (* x x))
(define (tan-cf x k)
(define (try next k)
(let ((result ( / (square x) (- (- (* 2 k) 1) next))))
(if (= k 2)
(/ x (- 1 result))
(try result (- k 1))
)
)
)
(try 0.0 k)
)