1.感知機模型

單層感知機是邏輯迴歸嗎_感知機


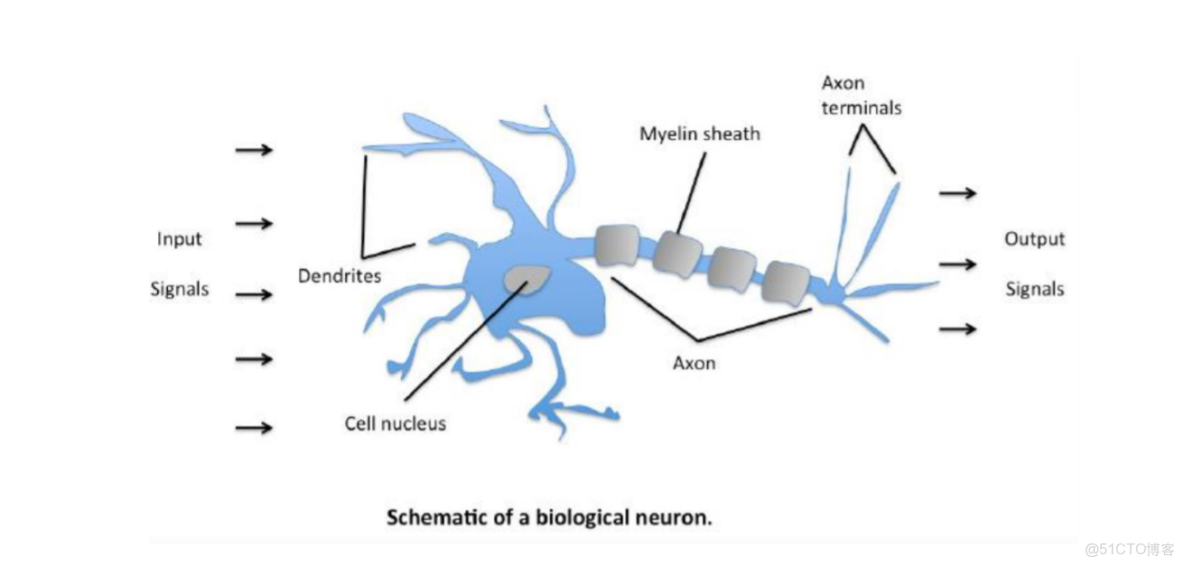
如圖為人體神經網絡圖，輸入信號從樹突傳入，在細胞核處彙總，輸出信號從軸突處傳出傳入其他神經元，從而構成了一個人體的神經網絡。而感知機其類似於一個神經元。

單層感知機是邏輯迴歸嗎_感知機_02

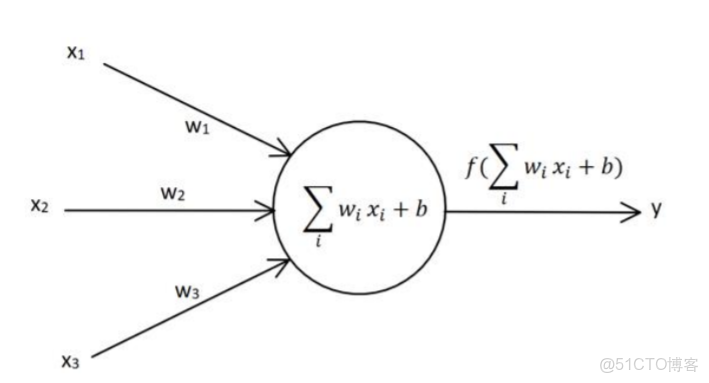
一個單層感知機與人體神經元類似，單層感知機是邏輯迴歸嗎_#機器學習_03為輸入結點，及神經元的輸入信號，單層感知機是邏輯迴歸嗎_#神經網絡_04為各輸入結點的權重，可以理解為神經元各個樹突的電阻，到達細胞核後通過進行彙總，通過一個激活函數處理後進行輸出。其中，w和b稱為感知機模型參數，w 叫做權重，b叫做偏置，f為激活函數，其表達式為：

單層感知機是邏輯迴歸嗎_#神經網絡_05

單層感知機是邏輯迴歸嗎_單層感知機是邏輯迴歸嗎_06


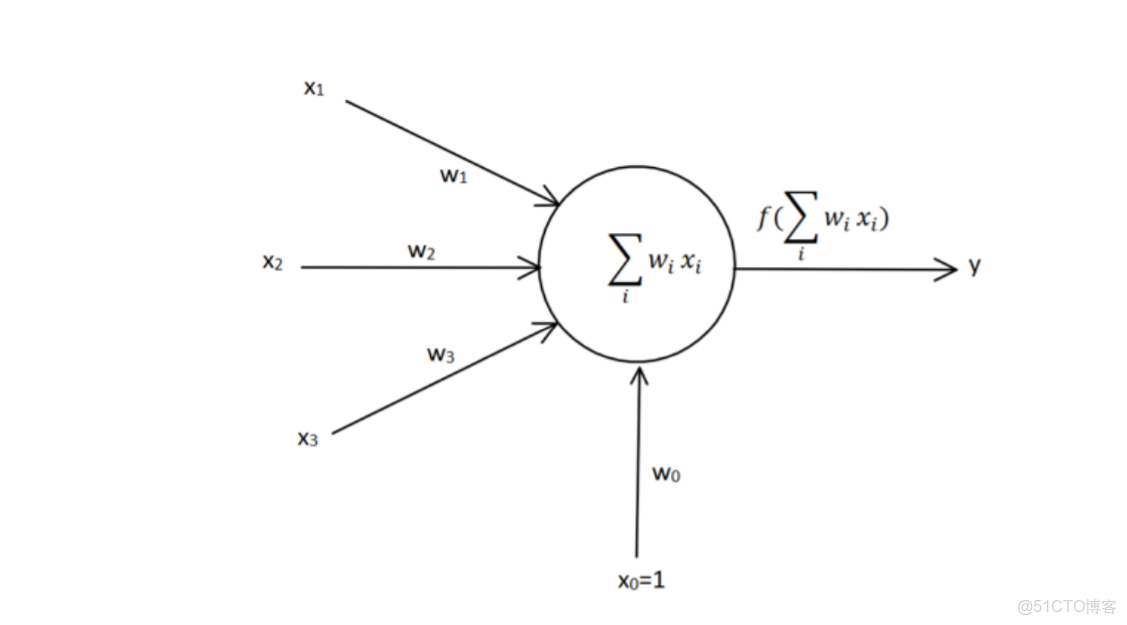
為了方便矩陣運算，將添加一個輸入恆為1的輸入信號x_{0},其對應的權重w_{0}即為偏置項b。多個感知機組合起來就構成了神經網絡。

 從感知機的激活函數的輸出來看，感知機可以處理過後的輸入信號進行分類。輸出為1是一類，輸出為-1又是一類。從幾何上來看，感知機學習的目標是對一個線性可分得數據集T求得一個能對T中的正負樣本進行正確劃分的一個超平面，參數w即為該超平面的法向量，偏置b為超平面的截距。這個超平面將數據集劃分為兩個部分，位於平面兩部分的點被分成了正負兩類。

2.感知機的學習策略

單層感知機是邏輯迴歸嗎_#機器學習_07恆成立。應為當單層感知機是邏輯迴歸嗎_單層感知機是邏輯迴歸嗎_08時，模型輸出值為1，而樣本實際值為-1，反之，當單層感知機是邏輯迴歸嗎_#神經網絡_09時，模型輸出為-1，而實際值為1，將兩種情況帶入可以得到單層感知機是邏輯迴歸嗎_#機器學習_07恆成立。由此，對於給定數據集T，其損失函數可定義為
單層感知機是邏輯迴歸嗎_感知機_11
M為誤分類點集合
x顯然損失函數是非負的，如果沒有誤分類點，損失函數值是0.誤分類點越少，損失函數就越小。
則要求參數w,b,就可以通過求解損失函數最小值點來得出參數。故而最小化問題進一步轉化為：
單層感知機是邏輯迴歸嗎_感知機_12

3.感知機的學習算法

感知機學習算法是由誤分類驅動的，具體採用隨梯度下降法。首先，任意選取一個超平面單層感知機是邏輯迴歸嗎_#神經網絡_13,然後採用梯度下降法不斷地極小化代價函數。極小化的過程不是一次使M中所有的誤分類點的梯度下降，而是隨機選取一個誤差分類點使其梯度下降。
假設誤分類樣本集合M固定時，那麼可以求得損失函數的梯度為：單層感知機是邏輯迴歸嗎_#機器學習_14
通過梯度下降w法梯度更新公式為：
單層感知機是邏輯迴歸嗎_感知機_15
所以感知機的學習算法為：
①選取初值單層感知機是邏輯迴歸嗎_單層感知機是邏輯迴歸嗎_16
②在數據集中選取單層感知機是邏輯迴歸嗎_#機器學習_17
③如果單層感知機是邏輯迴歸嗎_單層感知機是邏輯迴歸嗎_18則單層感知機是邏輯迴歸嗎_#機器學習_19
④轉置②，直至訓練集沒有誤分類點

4.代碼實現

import numpy as np
import matplotlib.pyplot as plt
import random
x=np.array([[1,3,3],
            [1,4,3],
            [1,1,1],
            [1,0,2]])
y=np.array([[1],
            [1],
            [-1],
            [-1]])
w=np.random.random([3,1])#生成一個3行1列的矩陣
lr=0.01#學習率
epochs=100#最大迭代次數
O=0
def plot():
    #正樣本
    x1 = [3,4]
    y1 = [3,3]
    #負樣本
    x2 = [1,0]
    y2 = [1,2]

    #計算分界線的斜率以及截距
    k = -w[1]/w[2]
    d = -w[0]/w[2]   #w0+w1*x+w2*y=0
    print('k=',k)
    print('d=',d)

    xdata=(0,5)

    plt.plot(xdata,xdata*k+d,'r')
    plt.scatter(x1,y1,c='b')
    plt.scatter(x2,y2,c='y')
    plt.show()

單層感知機是邏輯迴歸嗎_單層感知機是邏輯迴歸嗎_20
單層感知機是邏輯迴歸嗎_#機器學習_19

def gard():
    global x,y,lr,w
    O=np.sign(np.dot(x,w))#預測輸出
    #print(O)
    for i in range(x.shape[0]):
        a=x[i,:,np.newaxis].reshape(1,-1)
        b=O[i,:,np.newaxis].reshape(1,-1)
        if(np.dot(a,w)[0,0]*(y[i]-b)[0,0]<0):
            a=x[i,:,np.newaxis].reshape(1,-1)
            b=O[i,:,np.newaxis].reshape(1,-1)
            w_c=a.T.dot(y[i]-b)#
            w=w+lr*w_c#更新梯度
            break
    #print(w)
    return w
w=np.random.random([3,1])#生成一個3行1列的矩陣
for i in range(5000):
    w=gard()
    O=np.sign(np.dot(x,w))
    if(O==y).all():
        #print(O)
        #print(i)
    # if(i%10==0):
    #     plot()
    #     #print(w)
    #     #print(O) 
        break  
plot()
k= [-0.09968292]
d= [2.60720738]

單層感知機是邏輯迴歸嗎_#機器學習_22