1 ~> 初識紅黑樹:概念熟悉
紅黑樹也是一棵二叉搜索樹,其每個結點會增加一個存儲位(顏色存儲位),用來表示結點的顏色(兩種顏色),可以是紅色或者黑色(因此被稱為紅黑樹)。通過對任何一條從根到葉子的路徑上各個結點的顏色進行約束,紅黑樹確保沒有一條路徑會比其他路徑長出2倍,因而是接近平衡的,也就是説,紅黑樹是近似平衡的,這裏提前説一句,因為紅黑樹是近似平衡的,所以紅黑樹的插入的時間複雜度不存在最壞情況,就是O(logn),那麼下面這道題就可以直接給出答案了——
2 ~> 瞭解紅黑樹規則
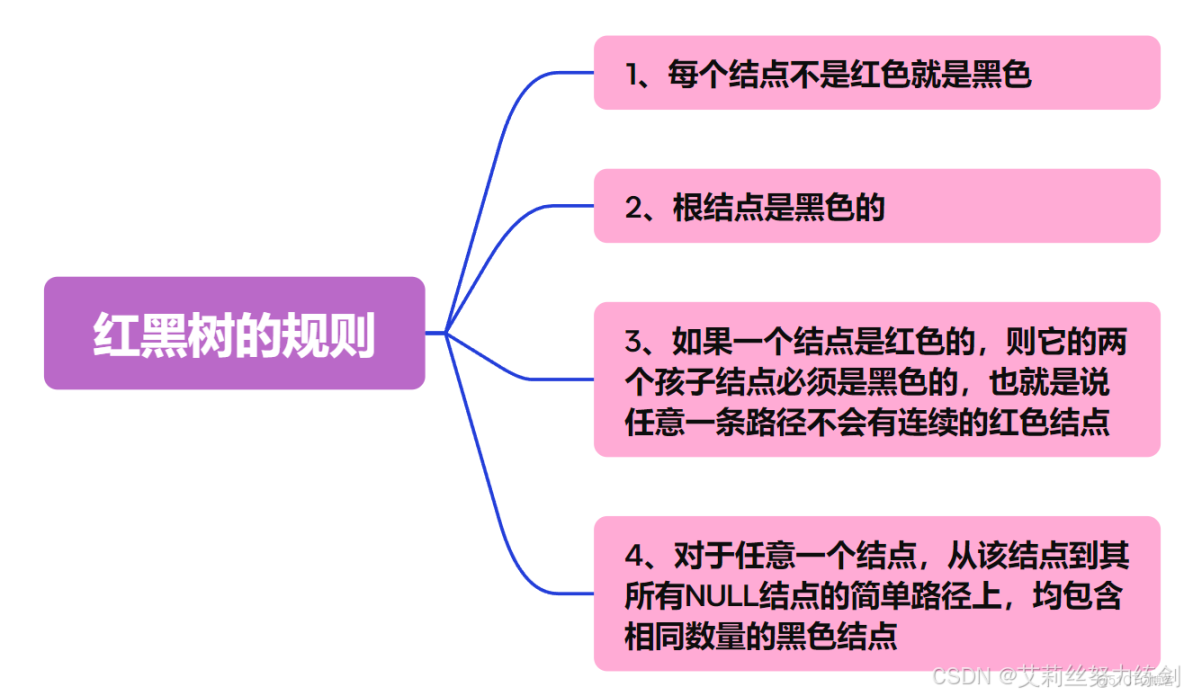
2.1 紅黑樹的四條規則
2.1.1 紅黑樹規則
2.1.2 結合圖示,體會紅黑樹規則
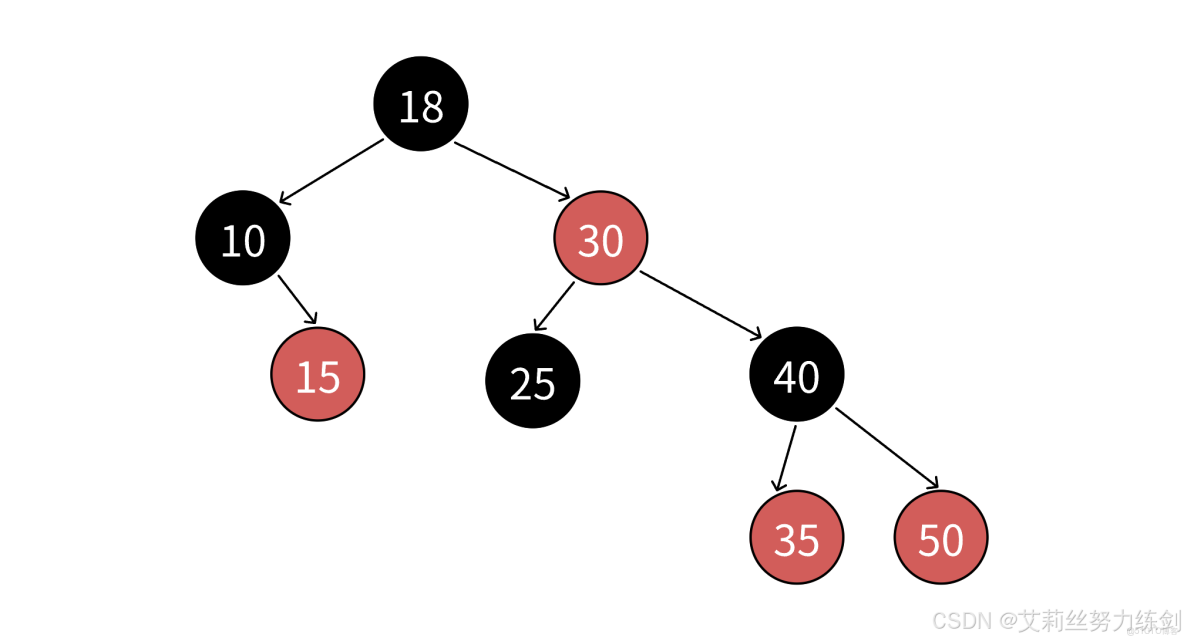
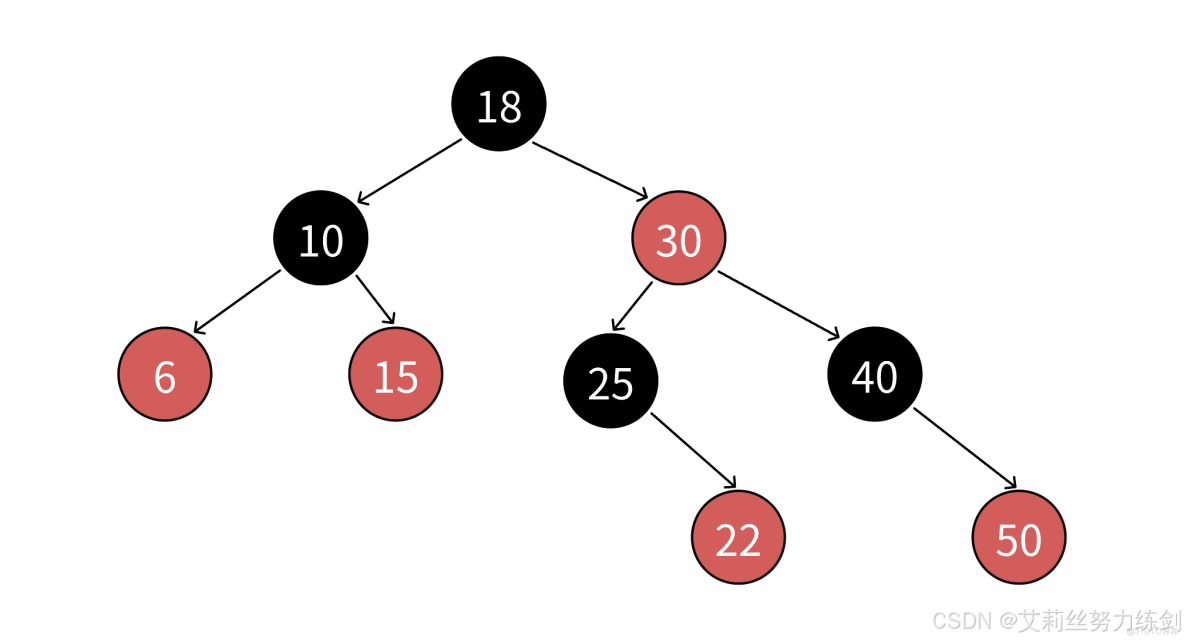
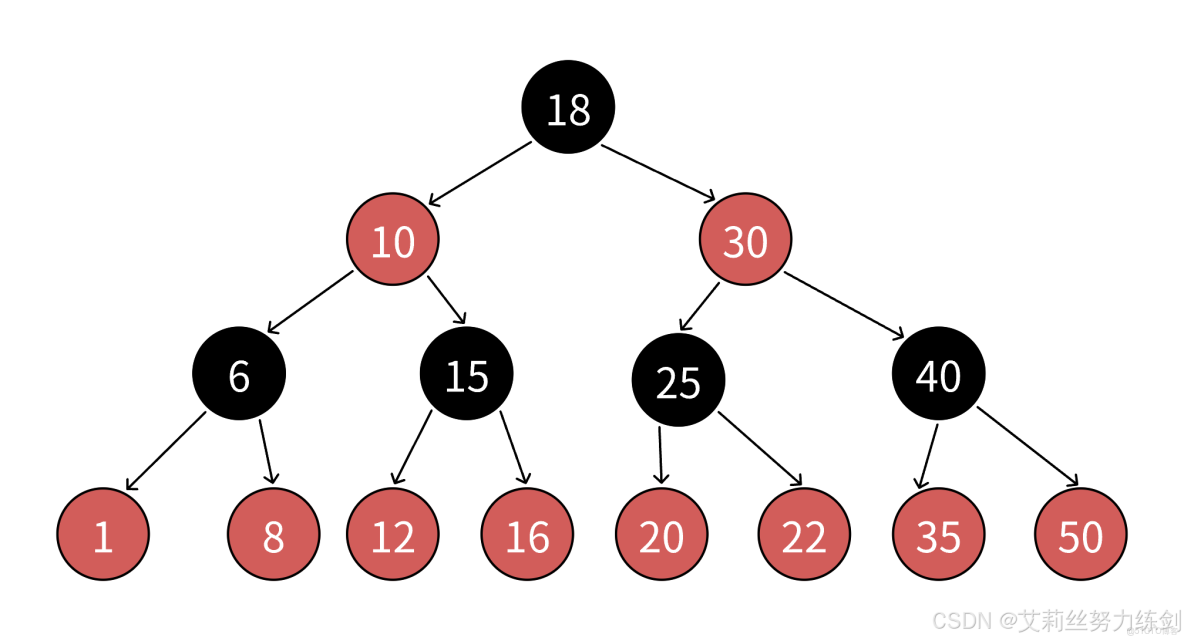
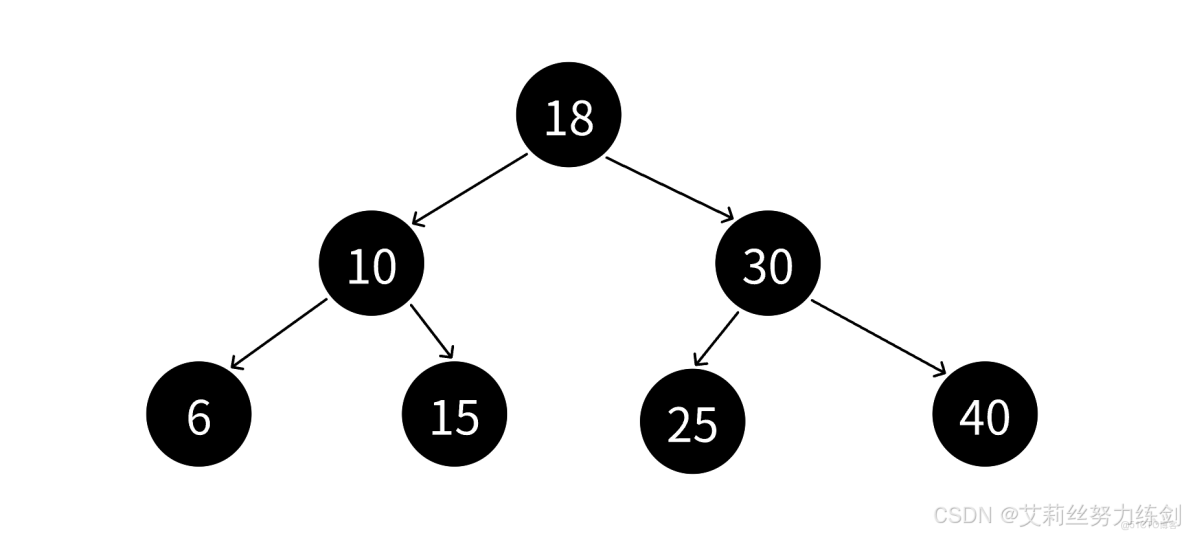
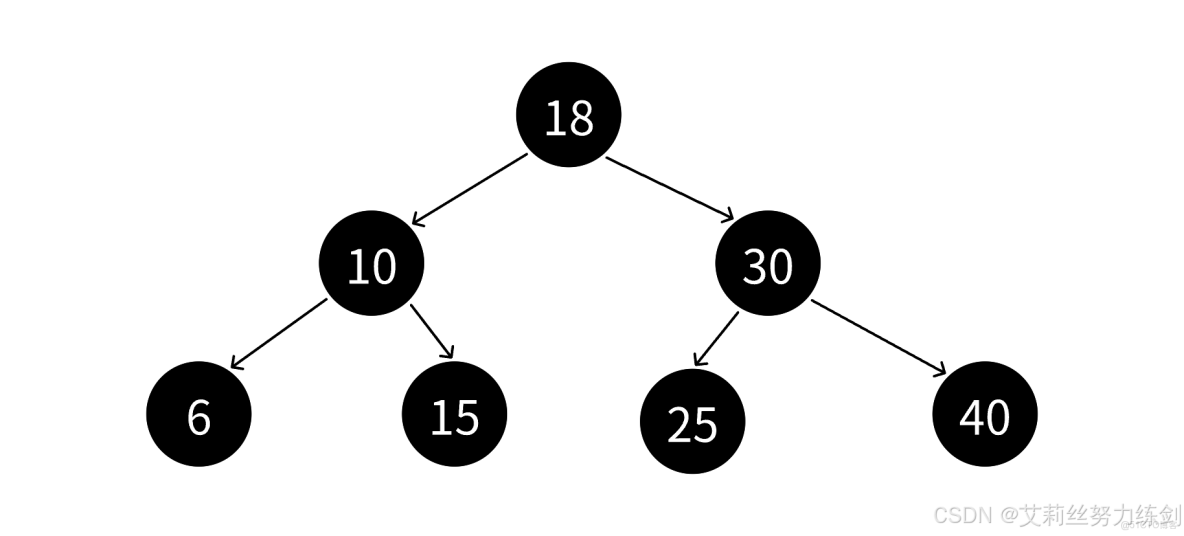
我們觀察幾張紅黑樹的圖大家就能有更進一步的體會了——
2.1.3 結合圖例,理解紅黑樹的路徑數量問題:NIL
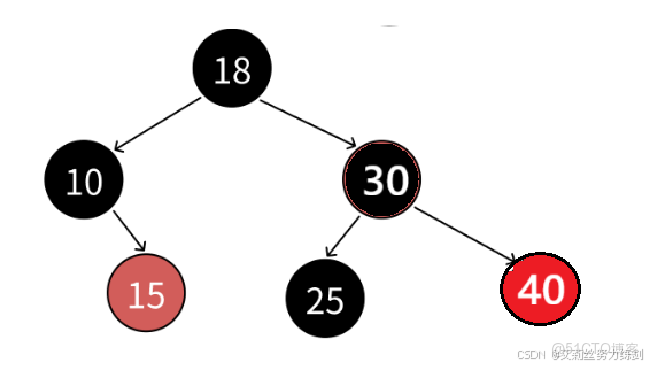
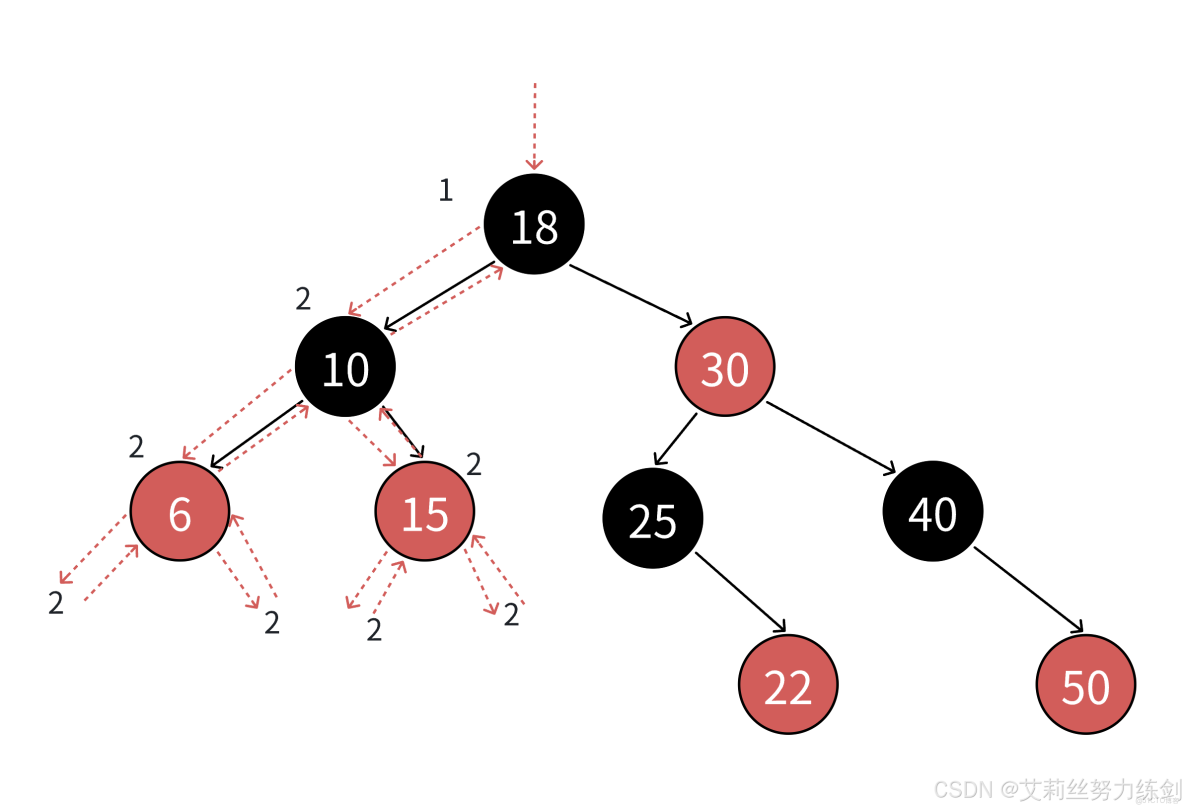
我們以上面這張圖為例,艾莉絲這裏考考大家,上面的紅黑樹裏面有幾條路徑?
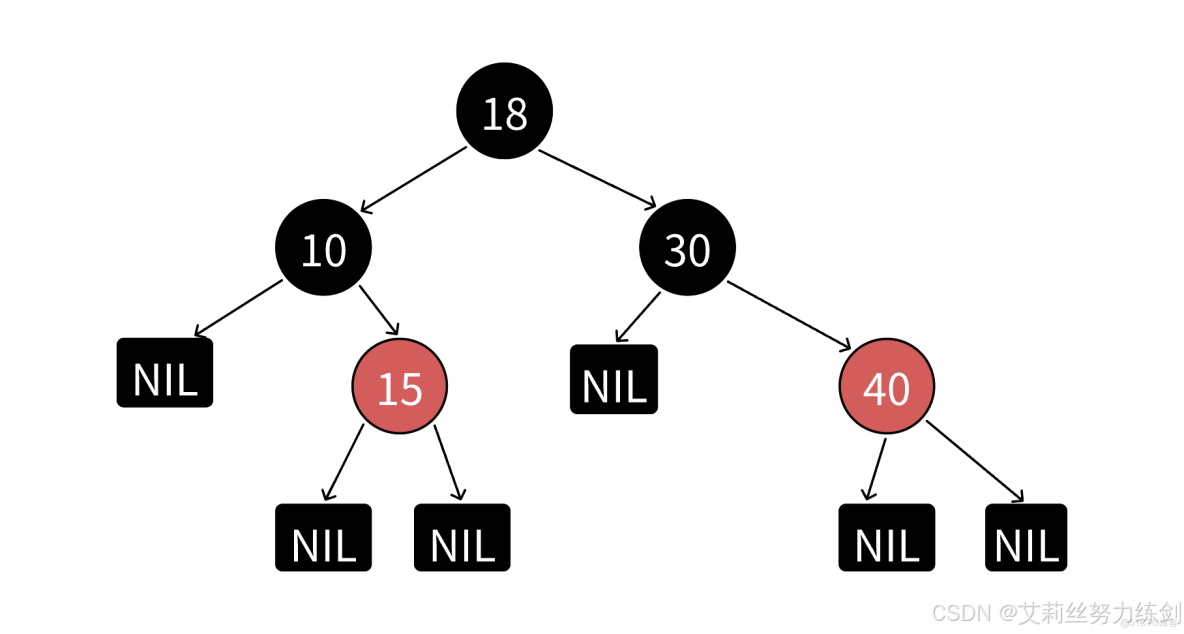
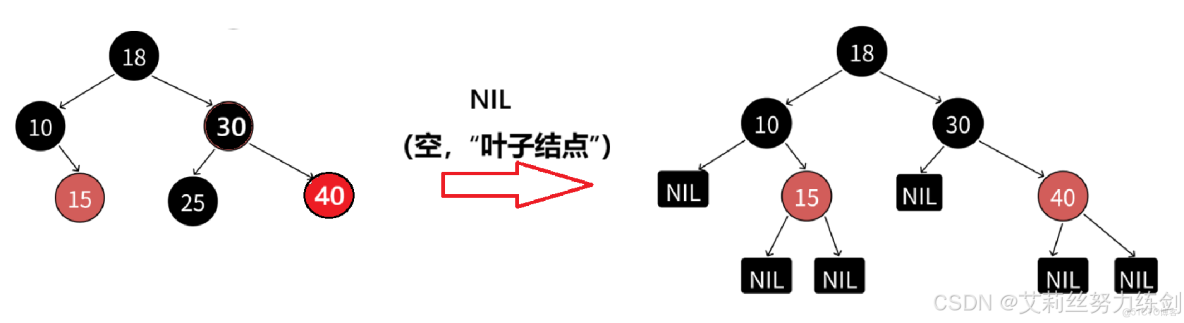
4條?不對哦!這裏實際上有6條路徑~~~大家請看——
有人會問,這個NIL是啥?這個叫葉子節點,但是這個和我們二叉樹裏面的葉子結點不是同一個東西!這個葉子結點指的是空節點,比如上面的紅色節點15,不是真正的葉子結點,它下面還有兩個空節點,所以上面的黑色節點10、30還有個左孩子的NIL。
有人會問,這個NIL是啥?這個叫葉子節點,但是這個和我們二叉樹裏面的葉子結點不是同一個東西!這個葉子結點指的是空節點,比如上面的紅色節點15,不是真正的葉子結點,它下面還有兩個空節點,所以上面的黑色節點10、30還有個左孩子的NIL。
説明:《算法導論》等書籍上補充了一條每個葉子結點(NIL)都是黑色的規則。它這裏所指的葉子結點不是傳統的意義上的葉子結點,而是我們説的空結點,有些書籍上也把NIL叫做外部結點。NIL是為了方便準確的標識出所有路徑,《算法導論》在後續講解實現的細節中也忽略了NIL結點,所以我們知道—下這個概念即可。
2.2 紅黑樹是怎麼確保最長路徑不超過最短路徑的2倍的?
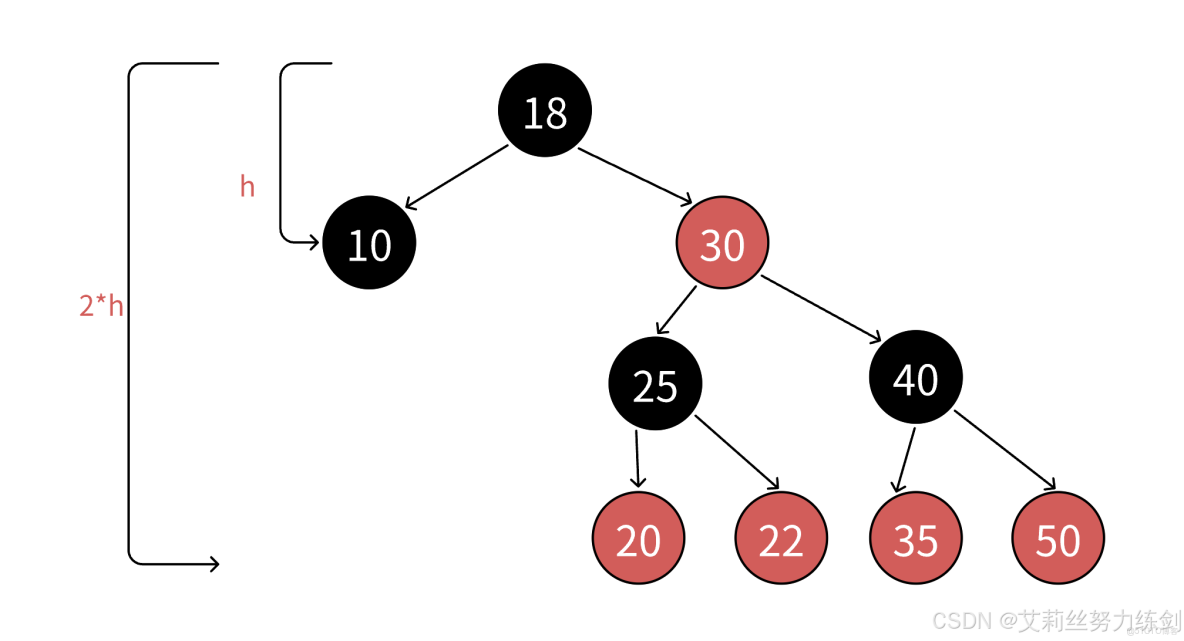
1、由規則4可知,從根到NULL結點的每條路徑都有相同數量的黑色結點,所以極端場景下,最短路徑就是全是黑色結點的路徑,假設最短路徑長度為bh(blackheight)。
2、由規則2和規則3可知,任意一條路徑不會有連續的紅色結點,所以極端場景下,最長的路徑就是一黑一紅間隔組成,那麼最長路徑的長度為2*bh。
3、綜合紅黑樹的4點規則而言,理論上的全黑最短路徑和一黑一紅的最長路徑並不是在每棵紅黑樹都所存在的。假設任意一條從根到NULL結點路徑的長度為x,那麼bh <= h <= 2*bh。
2.3 理解紅黑樹的效率
假設N是紅黑樹樹中結點數量,h最短路徑的長度,那麼2^h - 1 <= N < 2^(2 * h) - 1,由此推出h logN,也就意味着紅黑樹增刪查改最壞情況也就是走最長路徑2*logN,那麼時間複雜度還是
O(logN),像插入的情況艾莉絲在概念那裏就已經給出了一個例子,這裏不再贅述。
紅黑樹的表達相對AVL樹要抽象一些,AVL樹的直觀在於通過高度差控制了平衡,而紅黑樹是通過四條規則的顏色約束來間接實現近似平衡,他們效率都是同一檔次,但是相對而言,插入相同數量的結點,紅黑樹的旋轉次數是更少的,因為紅黑樹對平衡的控制沒那麼嚴格,所以我們比較常用的還是紅黑樹,因為紅黑樹的旋轉次數更少,效率還不比AVL樹低,因此實踐中紅黑樹用得比AVL樹多,這也是紅黑樹相比AVL樹的優勢。
3 ~> 實現紅黑樹
3.1 紅黑樹的結構實現我們用枚舉值來表示一下顏色——
我們實現一下紅黑樹的結構——
3.2 紅黑樹的插入問題以及插入的代碼實現
3.2.1 紅黑樹中插入一個值的大致過程
1、插入一個值按二叉搜索樹規則進行插入,插入後我們只需要觀察是否符合紅黑樹的4條規則。
2、如果是空樹插入,新增結點是黑色結點。如果是非空樹插入,新增結點必須紅色結點,因為非空樹插入,新增黑色結點就破壞了規則4,規則4是很難維護的。
3、非空樹插入後,新增結點必須紅色結點,如果父親結點是黑色的,則沒有違反任何規則,插入結束。
4、非空樹插入後,新增結點必須紅色結點,如果父親結點是紅色的,則違反規則3。進一步分析,c是紅色,p為紅,g必為黑,這三個顏色都固定了,關鍵的變化看u的情況,需要根據u分為以下幾種情況分別處理。
説明:下圖中假設我們把新增結點標識為c(cur),c的父親標識為p(parent),p的父親標識為g(grandfather),p的兄弟標識為u(uncle)。
3.2.2 三種情況
1、插入一個值按二叉搜索樹規則進行插入,插入後我們只需要觀察是否符合紅黑樹的4條規則。
2、如果是空樹插入,新增結點是黑色結點。如果是非空樹插入,新增結點必須紅色結點,因為非空樹插入,新增黑色結點就破壞了規則4,規則4是很難維護的。
3、非空樹插入後,新增結點必須紅色結點,如果父親結點是黑色的,則沒有違反任何規則,插入結束。
4、非空樹插入後,新增結點必須紅色結點,如果父親結點是紅色的,則違反規則3。進一步分析,c是紅色,p為紅,g必為黑,這三個顏色都固定了,關鍵的變化看u的情況,需要根據u分為以下幾種情況分別處理。
説明:下圖中假設我們把新增結點標識為c(cur),c的父親標識為p(parent),p的父親標識為g(grandfather),p的兄弟標識為u(uncle)。
3.2.2 三種情況
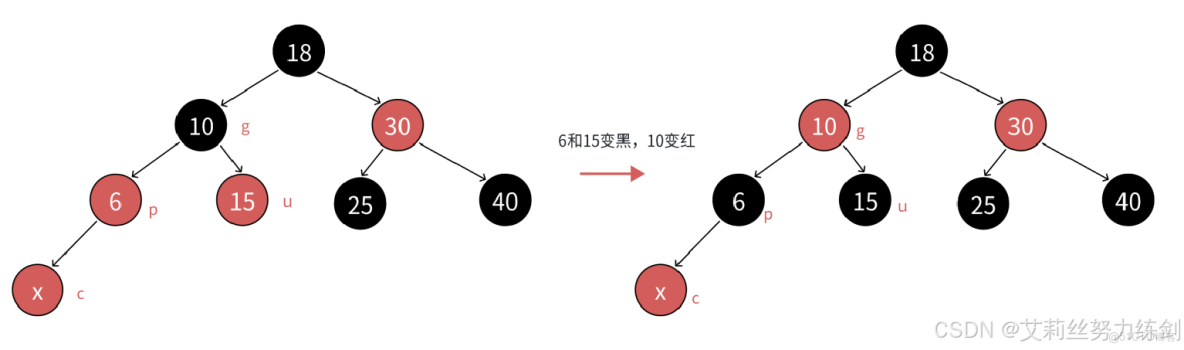
3.2.3 情況1:變色
c為紅,p為紅,g為黑,u存在且為紅,則將p和u變黑,g變紅。在把g當做新的c,繼續往上更新。
分析:因為p和u都是紅色,g是黑色,把p和u變黑,左邊子樹路徑各增加一個黑色結點,g再變紅,相當於保持g所在子樹的黑色結點的數量不變,同時解決了c和p連續紅色結點的問題,需要繼續往上更新是因為,g是紅色,如果g的父親還是紅色,那麼就還需要繼續處理;如果g的父親是黑色,則處理結束了;如果g就是整棵樹的根,再把g變回黑色。
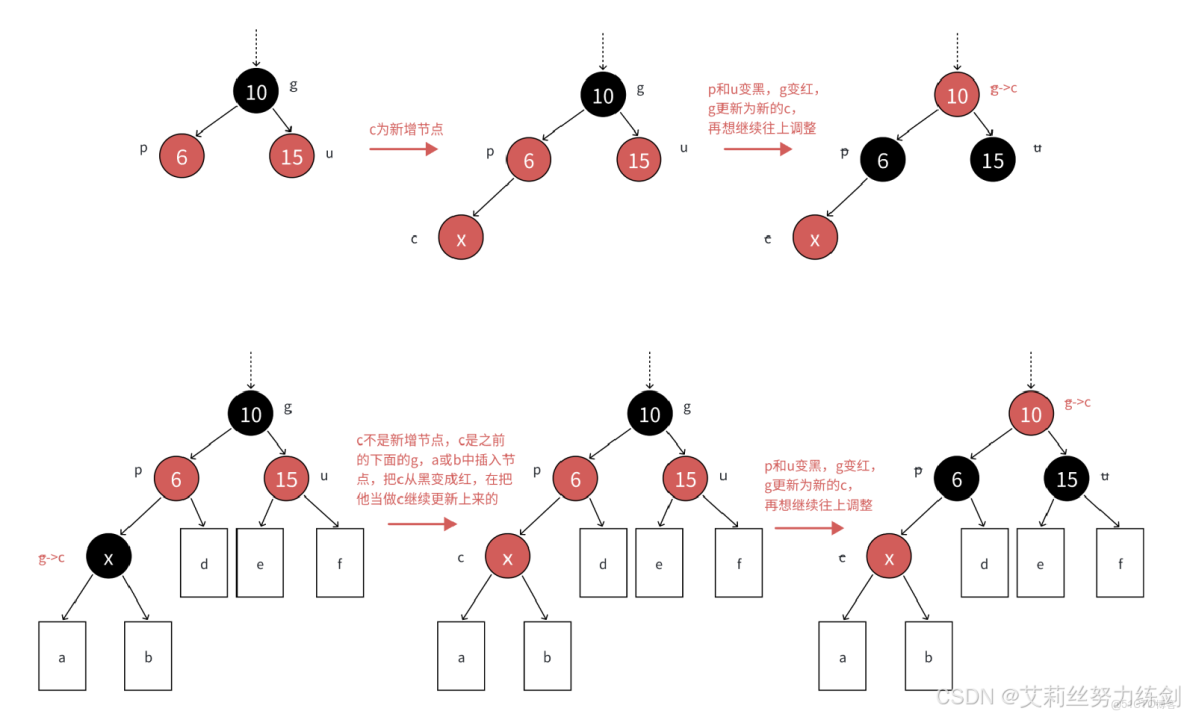
情況1只變色,不旋轉。所以無論c是p的左還是右,p是g的左還是右,都是上面的變色處理方式。
跟AVL樹類似,上圖向我們展示了一種具體情況,但是實際中需要這樣處理的有很多種情況。
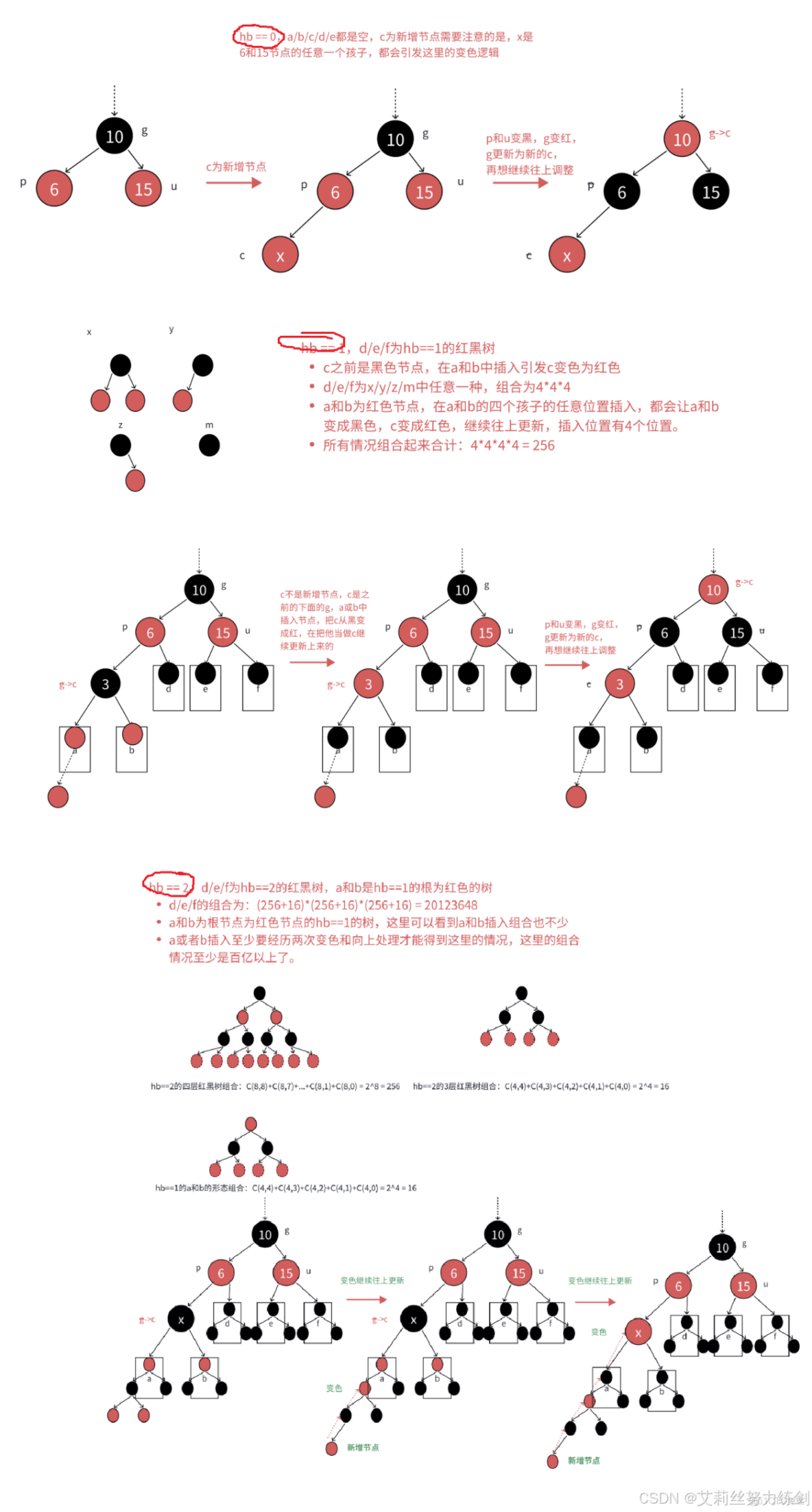
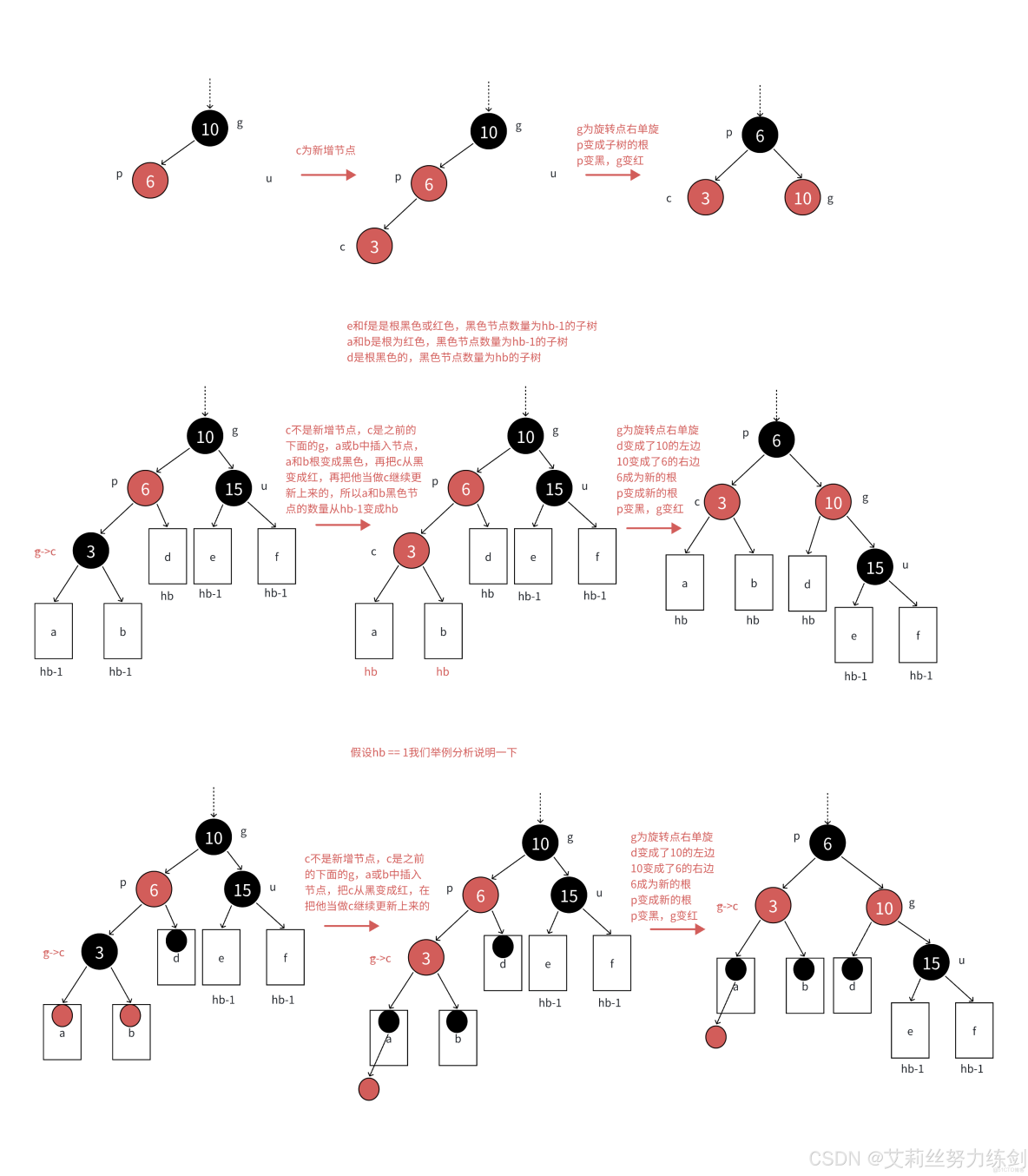
下圖將以上類似的處理進行了抽象表達,d / e / f代表每條路徑擁有hb個黑色結點的子樹,a / b代表每條路徑擁有hb - 1個黑色結點的根為紅的子樹,hb >= 0。
下圖則分別展示了hb == 0 / hb == 1 / hb == 2的具體情況組合分析——
當hb等於2時,這裏組合情況上百億種,這些樣例是幫助我們理解,不論情況多少種,有多麼複雜,處理方式都是一樣的,變色再繼續往上處理即可,所以我們只需要看抽象圖即可。
3.2.4 情況2:單旋 + 變色
c為紅,p為紅,g為黑,u不存在或者u存在且為黑,u不存在,則c一定是新增結點,u存在且為黑,則c一定不是新增,c之前是黑色的,是在c的子樹中插入,符合情況1,變色將c從黑色變成紅色,更新上來的。
分析:p必須變黑,才能解決,連續紅色結點的問題,u不存在或者是黑色的,這裏單純的變色無法解決問題,需要旋轉+變色。
如果p是g的左,c是p的左,那麼以g為旋轉點進行右單旋,再把p變黑,g變紅即可。p變成課這顆樹新的根,這樣子樹黑色結點的數量不變,沒有連續的紅色結點了,且不需要往上更新,因為p的父親是黑色還是紅色或者空都不違反規則。
如果p是g的左,c是p的左,那麼以g為旋轉點進行右單旋,再把p變黑,g變紅即可。p變成課這顆樹新的根,這樣子樹黑色結點的數量不變,沒有連續的紅色結點了,且不需要往上更新,因為p的父親是黑色還是紅色或者空都不違反規則。
如果p是g的右,c是p的右,那麼以g為旋轉點進行左單旋,再把p變黑,g變紅即可。p變成課這顆樹新的根,這樣子樹黑色結點的數量不變,沒有連續的紅色結點了,且不需要往上更新,因為p的父親是黑色還是紅色或者空都不違反規則。
3.2.5 情況3:雙旋 + 變色
c為紅,p為紅,g為黑,u不存在或者u存在且為黑,u不存在,則c一定是新增結點,u存在且為黑,則c一定不是新增,c之前是黑色的,是在c的子樹中插入,符合情況1,變色將c從黑色變成紅色,更新上來的。
分析:p必須變黑,才能解決,連續紅色結點的問題,u不存在或者是黑色的,這裏單純的變色無法解決問題,需要旋轉+變色。
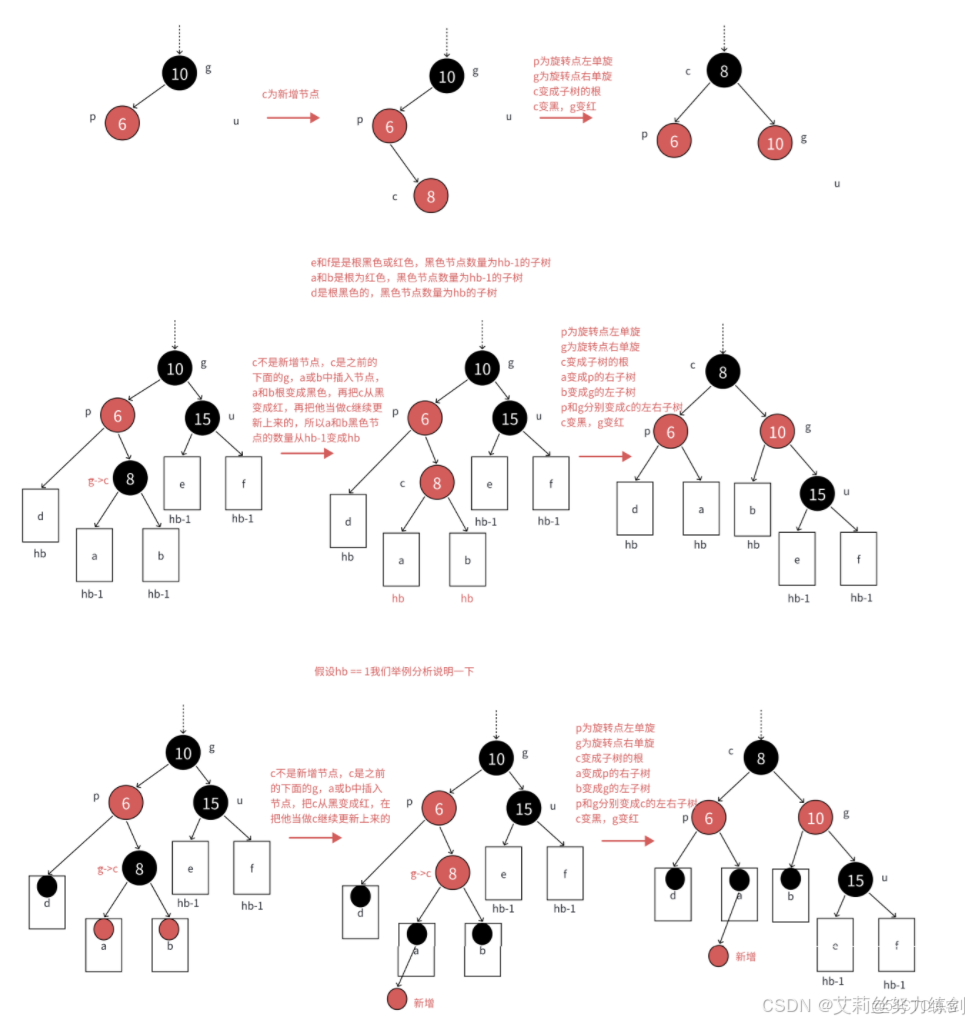
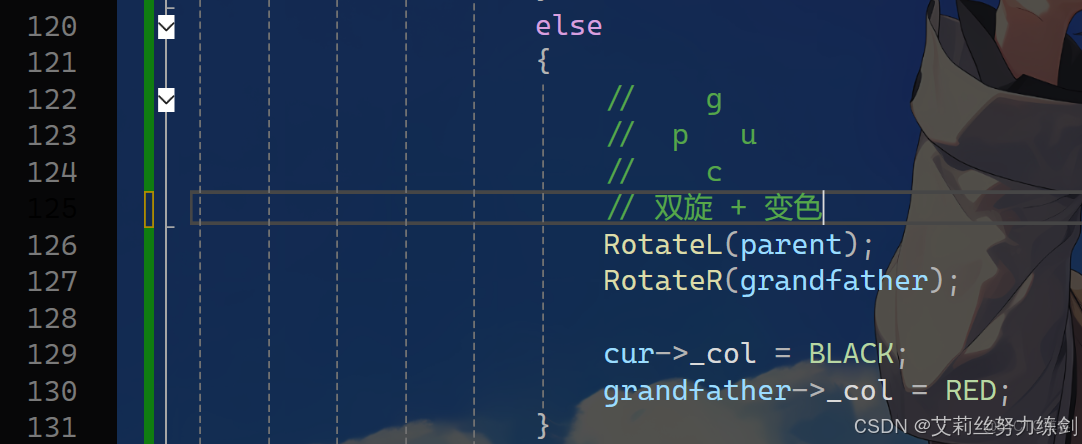
如果p是g的左,c是p的右,那麼先以p為旋轉點進行左單旋,再以g為旋轉點進行右單旋,再把c變
黑,g變紅即可。c變成課這顆樹新的根,這樣子樹黑色結點的數量不變,沒有連續的紅色結點了,且不需要往上更新,因為c的父親是黑色還是紅色或者空都不違反規則。
如果p是g的右,c是p的左,那麼先以p為旋轉點進行右單旋,再以g為旋轉點進行左單旋,再把c變
黑,g變紅即可。c變成課這顆樹新的根,這樣子樹黑色結點的數量不變,沒有連續的紅色結點了,且不需要往上更新,因為c的父親是黑色還是紅色或者空都不違反規則。
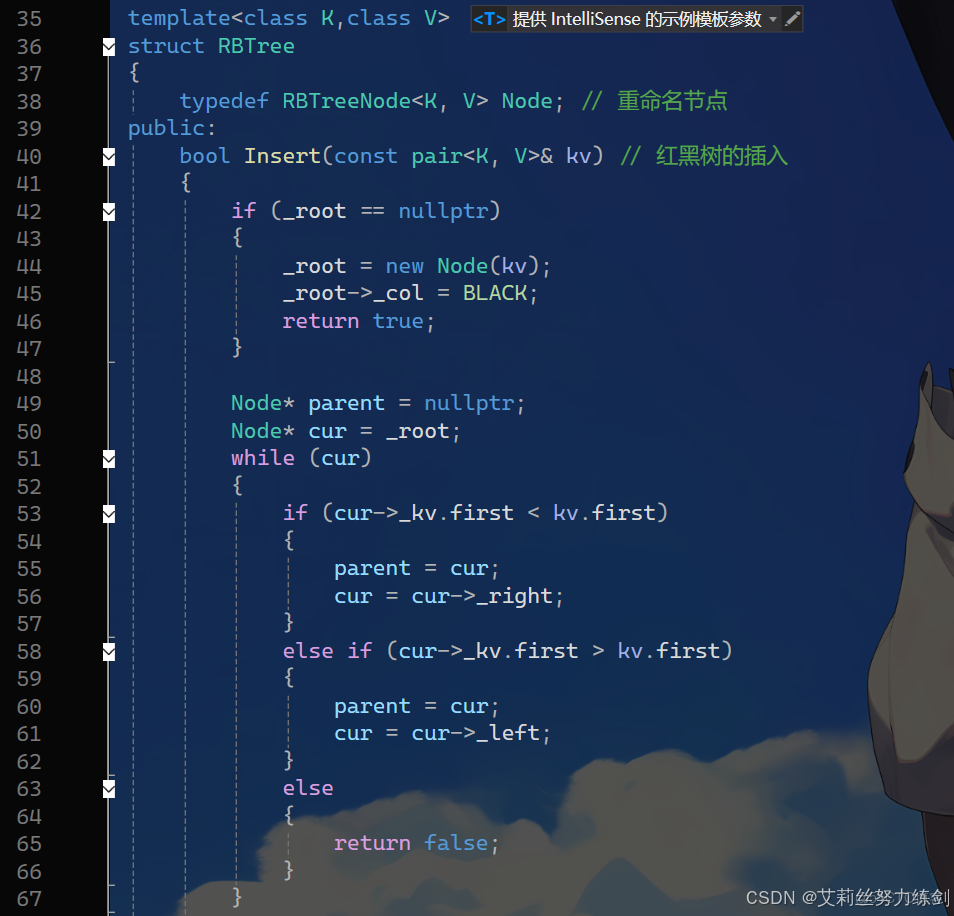
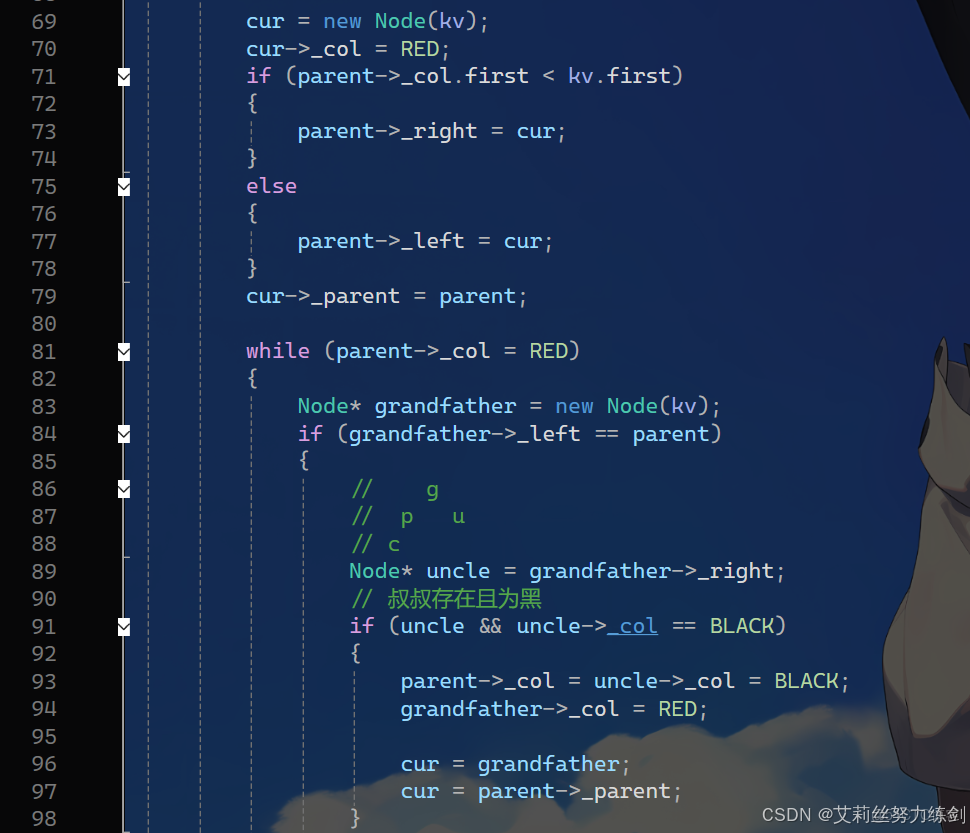
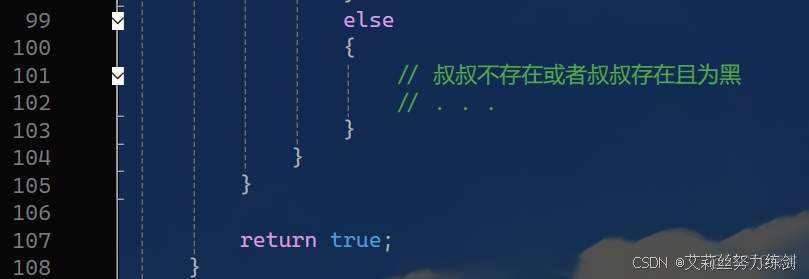
3.2.6 紅黑樹插入的代碼實現
代碼如下所示——
3.3 紅黑樹的旋轉
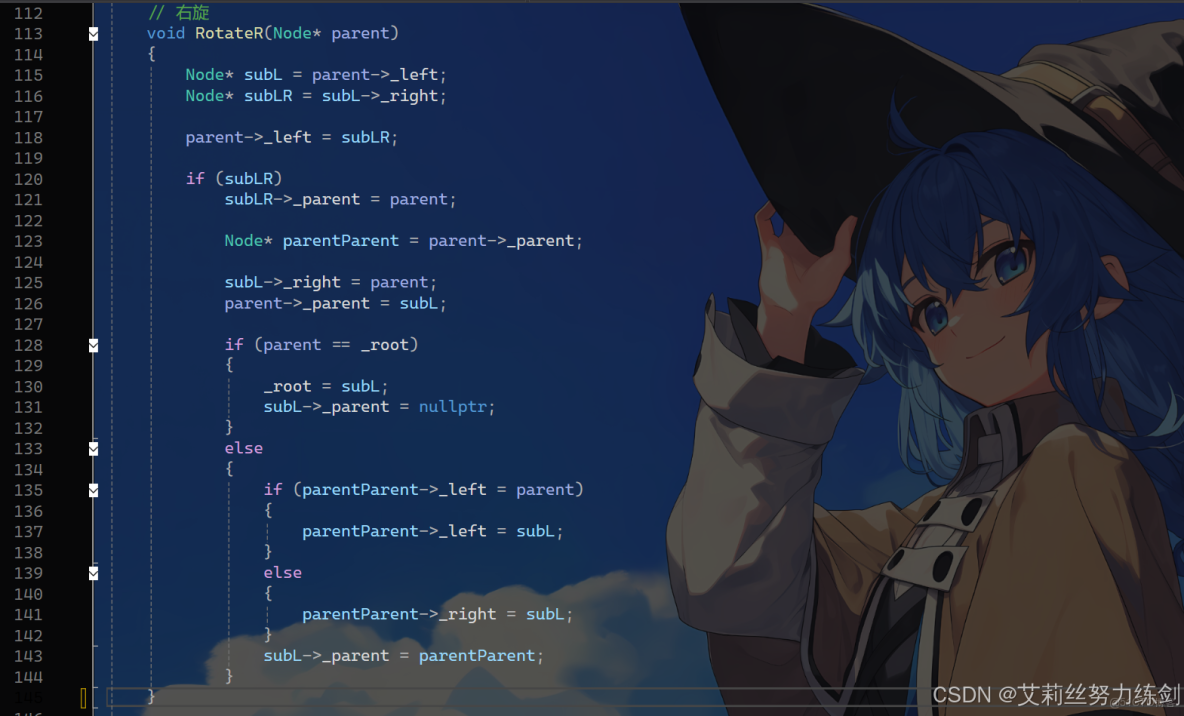
3.3.1 右旋
3.3.2 左旋
3.3.3 左右雙旋
3.3.4 右左雙旋
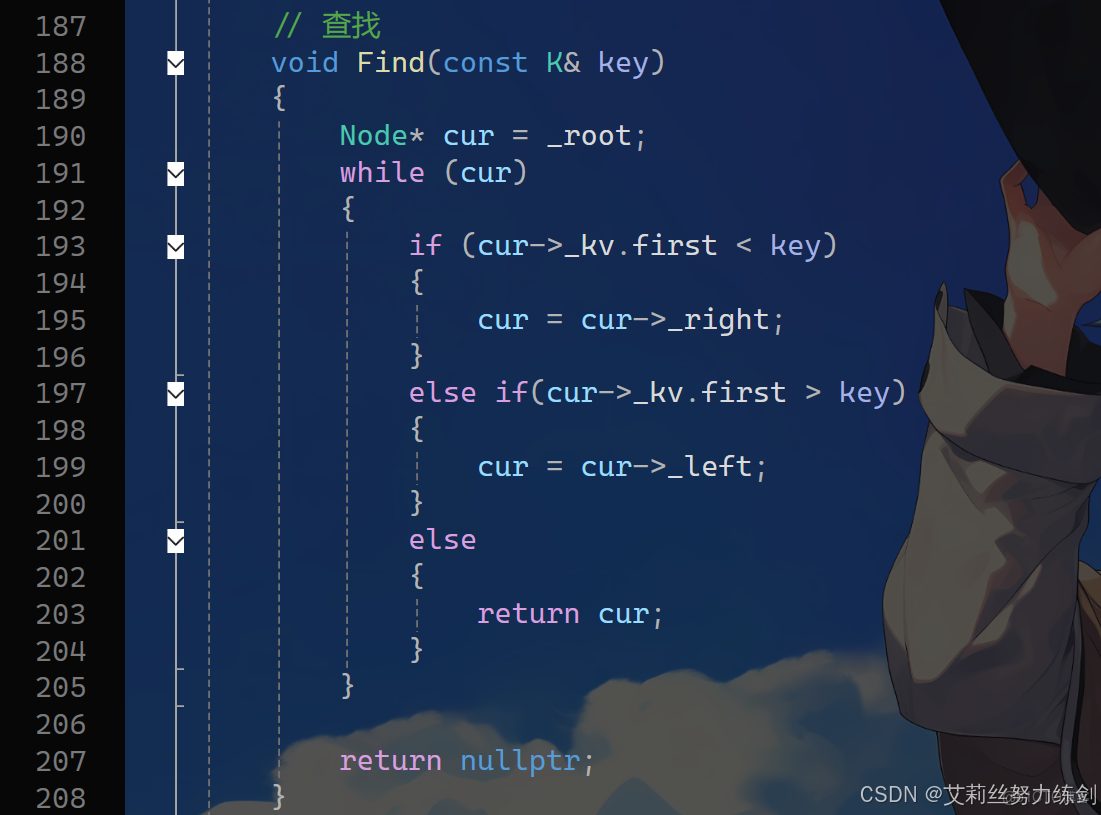
3.4 紅黑樹的查找問題
紅黑樹的查找就按搜索二叉樹的邏輯來實現就可以了,時間複雜度是O(logn)。
3.5 Size()
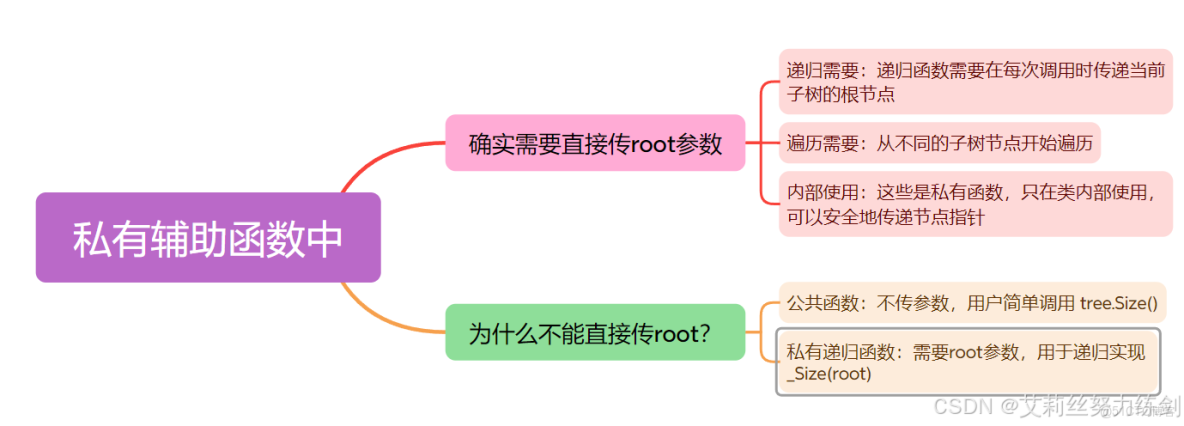
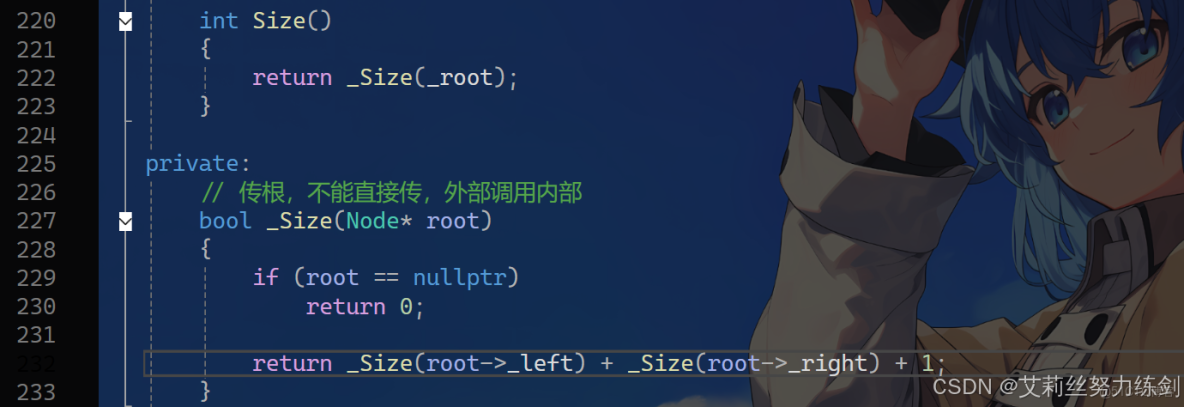
還是同樣的問題,這裏傳根不能直接傳,得從外部調用內部的函數完成傳根——
核心原因:封裝性 vs 遞歸需求的矛盾
3.5.1 公共接口:不需要傳root
public:
int Size() { return _Size(_root); } // 用户只需調用 tree.Size()
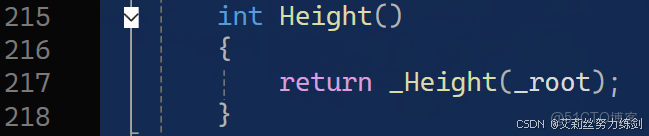
int Height() { return _Height(_root); } // 簡單、安全、易用
AI寫代碼
cpp
運行
3.5.2 私有實現:必須傳root
private:
int _Size(Node* root) { // 遞歸必須傳當前節點
if (root == nullptr) return 0;
return _Size(root->_left) + _Size(root->_right) + 1; // 遞歸調用
}
AI寫代碼
cpp
運行
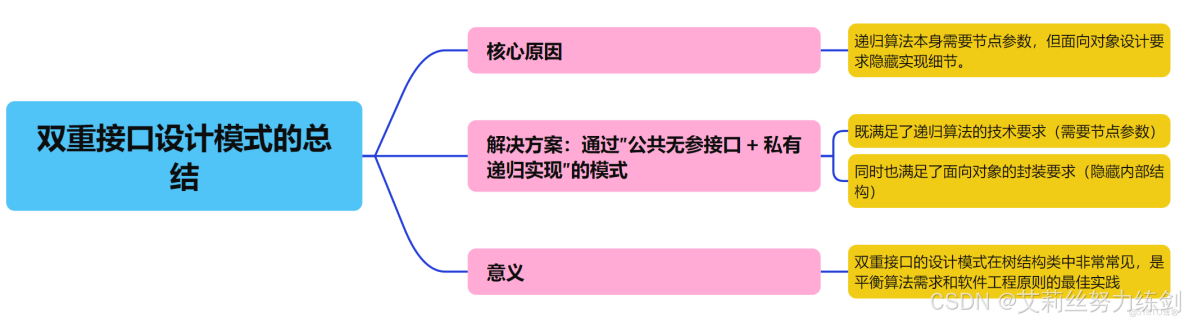
3.5.3 解決方案:雙重接口設計
因此我們的解決方案如下——
3.5.3.1 公共層(面向用户)
// 用户看到的簡單接口
tree.Size(); // 不需要參數
tree.Height(); // 直接使用
tree.IsBalanceTree();
AI寫代碼
cpp
運行
3.5.3.2 私有層(內部遞歸)
// 遞歸實現的輔助函數
_Size(root); // 需要節點參數
_Height(root); // 支持遞歸遍歷
_IsBalanceTree(root);
AI寫代碼
cpp
運行
3.5.4 為什麼要設計成雙重接口?
// 方案1:讓用户傳root(不好)
tree.Size(someNode); // 用户可能傳錯節點,不安全
// 方案2:放棄遞歸(不好)
// 用迭代實現Size(),但代碼複雜,性能可能更差
// 方案3:暴露_root(很不好)
tree._Size(tree._root); // 破壞封裝,會很危險,不安全
AI寫代碼
cpp3.5.5 總結
3.5.6 Size()雙重接口設計實現
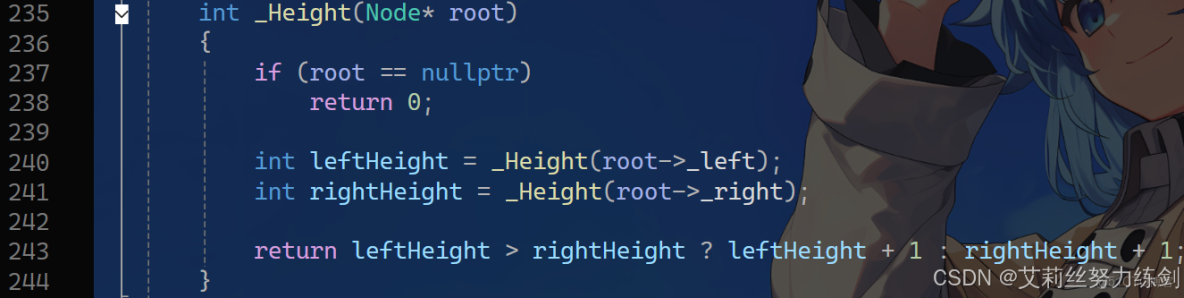
3.6 Height()
外部(public)——
內部(private)——
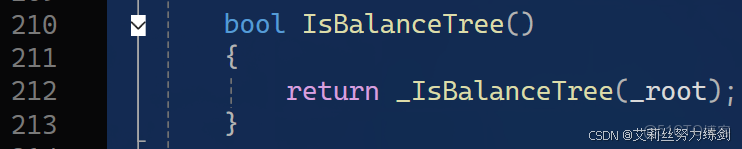
3.7 IsBalanceTree()
外部(public)——
內部(private)——
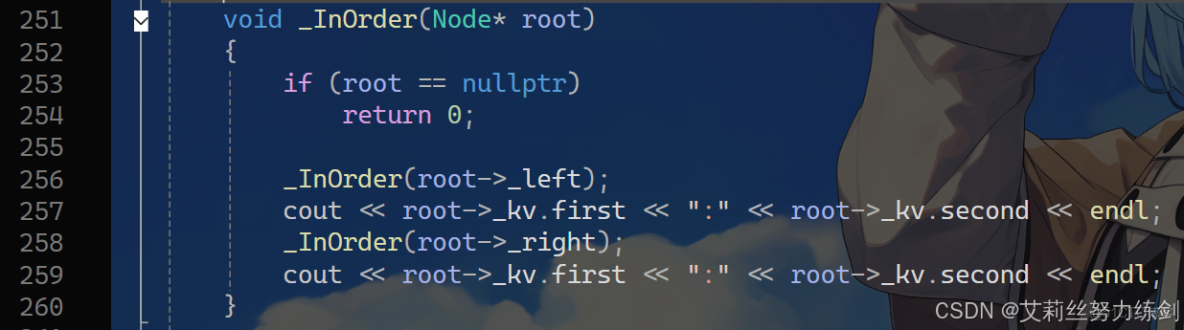
3.8 中序遍歷:InOrder()
外部(public)——
內部(private)——
3.9 驗證紅黑樹
這裏獲取最長路徑和最短路徑,檢查最長路徑不超過最短路徑的2倍是不可行的,因為就算滿足這個條件,紅黑樹也可能顏色不滿足規則,當前暫時沒出問題,後續繼續插入還是會出問題的。所以我們還是去檢查4點規則,滿足這4點規則,一定能保證最長路徑不超過最短路徑的2倍。
1、規則1枚舉顏色類型,天然實現保證了顏色不是黑色就是紅色。
2、規則2直接檢查根即可。
3、規則3前序遍歷檢查,遇到紅色結點查孩子不太方便,因為孩子有兩個,且不一定存在,反過來檢查父親的顏色就方便多了,即孩子不一定存在,父親一定存在。
4、規則4前序遍歷,遍歷過程中用形參記錄根節點到當前結點的blackNum(黑色結點數量),前序遍歷遇到黑色結點就++blackNum,走到空就計算出了一條路徑的黑色結點數量。再任意一條路徑黑色結點數量作為參考值,依次比較即可。
3.10 紅黑樹的刪除
和AVL樹那裏一樣,紅黑樹這裏的刪除我們也不做講解——
完整代碼示例與實踐演示
RBTree.h:
#pragma once
#include<iostream>
using namespace std;
#include<assert.h>
// 枚舉值表示顏色
// 保障不是黑色就是紅色
enum Color
{
BLACK,
RED
};
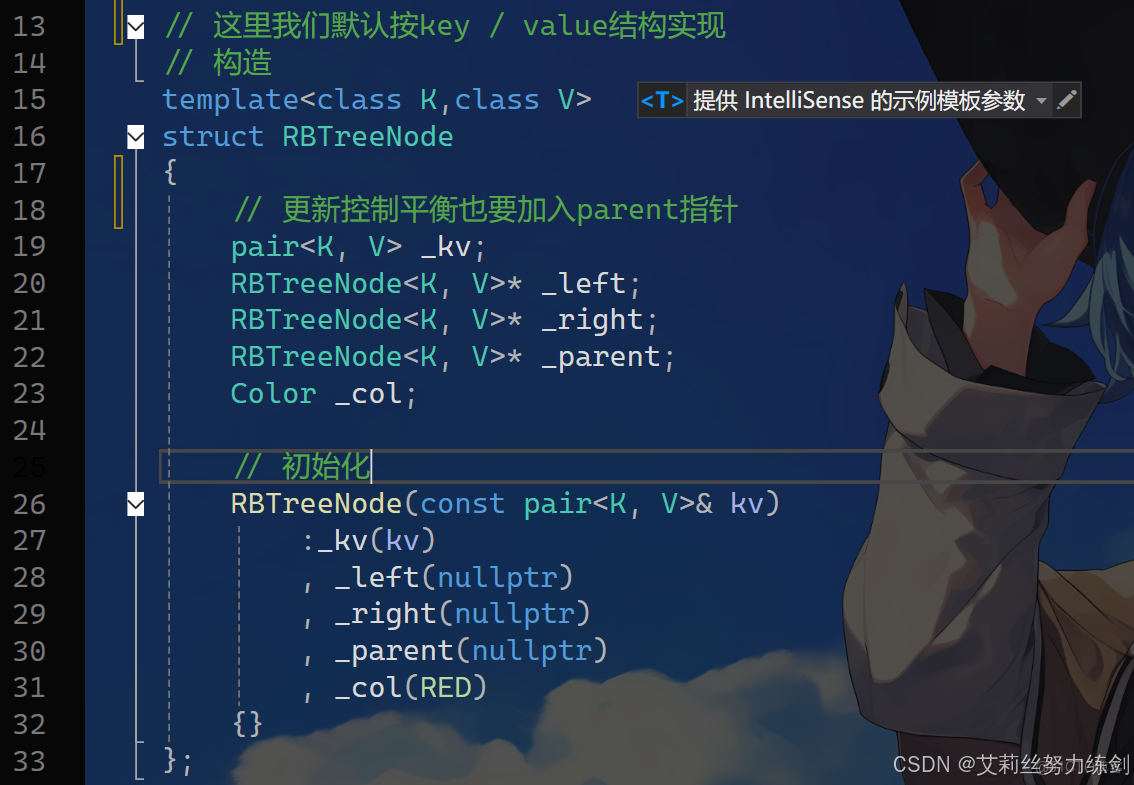
// 這裏我們默認按key / value結構實現
// 構造
template<class K,class V>
struct RBTreeNode
{
// 更新控制平衡也要加入parent指針
pair<K, V> _kv;
RBTreeNode<K, V>* _left;
RBTreeNode<K, V>* _right;
RBTreeNode<K, V>* _parent;
Color _col;
// 初始化
RBTreeNode(const pair<K, V>& kv)
:_kv(kv)
, _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _col(RED)
{}
};
template<class K,class V>
struct RBTree
{
typedef RBTreeNode<K, V> Node; // 重命名節點
public:
bool Insert(const pair<K, V>& kv) // 紅黑樹的插入
{
if (_root == nullptr)
{
_root = new Node(kv);
_root->_col = BLACK;
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
// 插入的是紅色的節點(新增)
cur = new Node(kv);
cur->_col = RED;
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
while (parent && parent->_col == RED)
{
Node* grandfather = parent->_parent;
if (grandfather->_left == parent)
{
// g
// p u
// c
Node* uncle = grandfather->_right;
// 叔叔存在且為黑
if (uncle && uncle->_col == RED)
{
// 變色 + 繼續往上處理
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;
}
else
{
// 叔叔不存在或者叔叔存在且為黑
// g
// p u
// c
// 單旋 + 變色
if (cur == parent->_left)
{
RotateR(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
// g
// p u
// c
// 雙旋 + 變色
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
else
{
// g
// u p
Node* uncle = grandfather->_left;
// 叔叔存在且為紅->變色即可
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
// 繼續往上處理
cur = grandfather;
parent = cur->_parent;
}
else
{
// 情況二:叔叔不存在或者存在且為黑
// 旋轉 + 變色
// g
// u p
// c
if (cur == parent->_right)
{
RotateL(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
// g
// u p
// c
RotateR(parent);
RotateL(grandfather);
grandfather->_col = RED;
}
break;
}
}
}
_root->_col = BLACK; // 不去判斷,直接變成黑的
return true;
}
// -------------旋轉----------------
// 右旋
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
subLR->_parent = parent;
Node* parentParent = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
if (parent == _root)
{
_root = subL;
subL->_parent = nullptr;
}
else
{
if (parentParent->_left == parent)
{
parentParent->_left = subL;
}
else
{
parentParent->_right = subL;
}
subL->_parent = parentParent;
}
}
// 左旋
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
// 處理 subRL 與 parent 的關係
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
Node* parentParent = parent->_parent;
// 處理 subR 與 parent 的關係
subR->_left = parent;
parent->_parent = subR;
// 處理 subR 與 parentParent 的關係
if (parentParent == nullptr)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (parent == parentParent->_left)
{
parentParent->_left = subR;
}
else
{
parentParent->_right = subR;
}
subR->_parent = parentParent;
}
}
// 中序遍歷
void InOrder()
{
_InOrder(_root);
cout << endl;
}
// 查找
Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < key)
{
cur = cur->_right;
}
else if(cur->_kv.first > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
bool IsBalanceTree()
{
if (_root && _root->_col == RED)
return false;
// 最左路徑黑色節點的數量做參考值,去比較其他路徑
int left_bn = 0;
Node* cur = _root;
while (cur)
{
if (cur->_col == BLACK)
left_bn++;
cur = cur->_left; // 不加上會死循環
}
return _Checkcolor(_root, 0, left_bn);
}
int Height()
{
return _Height(_root);
}
int Size()
{
return _Size(_root);
}
private:
// 傳根,不能直接傳,外部調用內部
int _Size(Node* root)
{
if (root == nullptr)
return 0;
return _Size(root->_left) + _Size(root->_right) + 1;
}
int _Height(Node* root)
{
if (root == nullptr)
return 0;
int leftHeight = _Height(root->_left);
int rightHeight = _Height(root->_right);
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}
// root_cur_bn 根節點到當前節點路徑上的黑色節點的數量
// 前序遞歸
bool _Checkcolor(Node* root, int root_cur_bn,const int left_bn)
{
if (root == nullptr)
{
// 檢查每條路徑的黑色節點數量
if (root_cur_bn != left_bn)
{
cout << "黑色節點的數量不相等" << endl;
return false;
}
return true;
}
if (root->_col == BLACK)
{
root_cur_bn++;
}
// 檢查連續的紅色節點
if (root->_col == RED && root->_parent && root->_parent->_col == RED)
{
cout << root->_kv.first << "存在連續的紅色節點" << endl;
return false;
}
return _Checkcolor(root->_left, root_cur_bn, left_bn)
&& _Checkcolor(root->_right, root_cur_bn, left_bn);
}
int _InOrder(Node* root)
{
if (root == nullptr)
return 0;
_InOrder(root->_left);
//cout << root->_kv.first << ":" << root->_kv.second << endl;
cout << root->_kv.first << " ";
_InOrder(root->_right);
////cout << root->_kv.first << ":" << root->_kv.second << endl;
}
private:
Node* _root = nullptr;
};
AI寫代碼
cpp
運行
Tree.cpp:
#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<vector>
using namespace std;
#include"RBTree.h"
void TestRBTree1()
{
RBTree<int, int>t;
// 常規的測試用例
int a[] = { 4,2,6,1,3,5,15,7,16,14 };
for (auto e : a)
{
if (e == 7)
{
int i = 0;
}
t.Insert({ e,e });
cout << "Insert:" << e << "->";
t.InOrder();
}
t.InOrder();
//cout << t.IsBalanceTree() << endl;
}
// 插入一堆隨機值,測試平衡,順便測試一下高度和性能
void TestRBTree2()
{
const int N = 1000000;
vector<int> v;
v.reserve(N);
srand(time(0));
for (size_t i = 0; i < N; i++)
{
v.push_back(rand() + i);
}
size_t begin2 = clock();
RBTree<int, int> t;
for (auto e : v)
{
t.Insert(make_pair(e, e));
}
size_t end2 = clock();
cout << "Insert:" << end2 - begin2 << endl;
cout << t.IsBalanceTree() << endl;
cout << "Height:" << t.Height() << endl;
cout << "Size:" << t.Size() << endl;
size_t begin1 = clock();
// 確定在的值
/*for (auto e : v)
{
t.Find(e);
}*/
// 隨機值
for (size_t i = 0; i < N; i++)
{
t.Find((rand() + i));
}
size_t end1 = clock();
cout << "Find:" << end1 - begin1 << endl;
}
int main()
{
//TestRBTree1();
TestRBTree2();
return 0;
}
AI寫代碼
cpp
運行
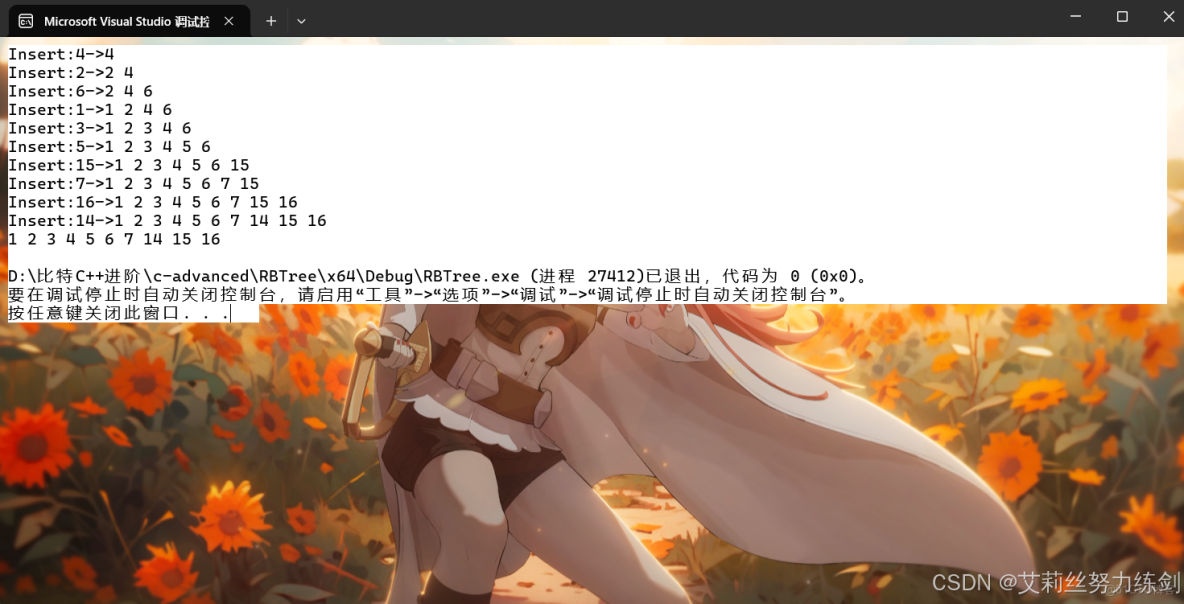
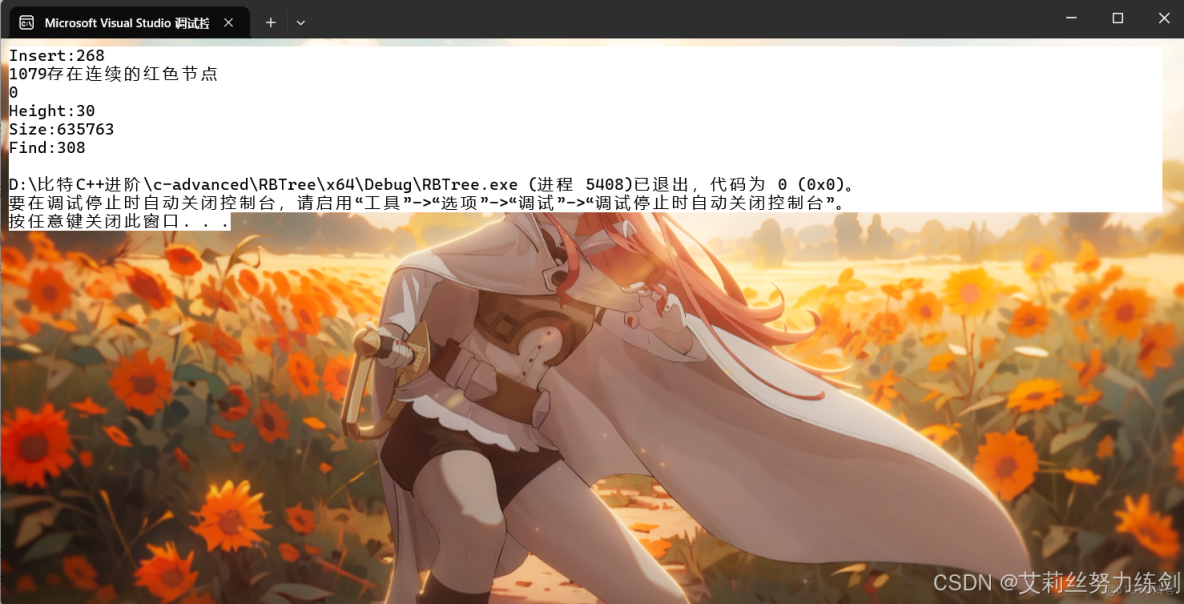
運行結果
TestRBTree1()
TestRBTree2()