1. 簡介

Generalized-ICP（簡稱 GICP）由 Aleksandr Segal 等人提出（R: Robotics: Science and Systems 2009），它把經典 ICP（point-to-point）和 point-to-plane ICP 統一到一個 概率/協方差驅動的最小二乘框架，通過為每個點建立局部協方差矩陣並使用馬氏距離（Mahalanobis distance）來衡量配對誤差，從而在嘈雜、非均勻密度和局部平面結構多的場景中更穩健地估計剛性變換。

---

2. 算法背景與動機

• 經典 ICP（點到點）用歐氏距離最小化對應點間的差異，簡單但對噪聲、點密度差異、採樣方向不敏感。
• point-to-plane ICP 在目標點的法線方向上最小化距離（投影誤差），在近似平面結構上收斂更快、更準確，但需要可靠法線且只考慮目標表面局部結構單側信息。
• GICP 的動機是：兩邊（源點和目標點）都包含局部幾何信息（例如局部平面），應把這種不確定性用概率模型表達，並在配準時同時利用兩側信息，從而獲得更一致的誤差面和更魯棒的收斂。

---

3. 論文貢獻 / 創新點

1. 概率化統一視角：把點雲配準建模為對每對對應點以各自局部協方差為不確定性的聯合高斯分佈下的極大似然估計（MLE），從而統一點對點和點對面方法。
2. 局部協方差估計：為每個點估算局部協方差（採樣自其近鄰點集的協方差矩陣），以描述該點在空間中沿不同方向的幾何不確定性（例如局部平面會導致沿法線方向方差小、切平面方向方差大）。
3. 馬氏距離代價：使用 () 形式的代價（含兩側協方差），體現兩側不確定性融合；代價在局部近似為二次，更利於優化。
4. 比對傳統 ICP 的魯棒性：在複雜幾何形狀、噪聲、不同密度和部分視角變化下往往比純點到點或點到面更穩健，且對初值依賴性降低（通常）。許多後續工作以此為基準進行改進。

---

4. 需要解決的關鍵問題（GICP 針對哪些技術痛點）

• 如何同時利用源與目標點雲的局部結構特徵（而不是隻看單側法線）？
• 如何在誤差度量中將不同方向上的幾何不確定性量化併合理組合？
• 在最小化帶協方差的代價時，如何高效地線性化與求解（保持可用性）？
• 如何在存在噪聲、離羣點、採樣密度差的情況下仍然保證收斂性與準確性？

GICP 的回答是：對每個點估計局部協方差並將其組合到誤差權重中，代價採用馬氏距離形式，然後使用傳統的最小化工具（線性化、解線性系統）來求解變換。

---

5. 論文提出的算法流程

下面把 GICP 的流程寫成偽代碼 / 步驟，便於理解實現要點。

1. 輸入：源點雲 ，目標點雲 ，初始變換 。
2. 為每個點估計局部協方差：對 中每個 用其 近鄰計算協方差 ；對 中每個 計算 （通常對原始點雲各自獨立計算）。
3. 外循環（ICP 風格）：

• 以當前變換 將源點雲 變換到目標座標系：
  
• 對每個 找到其對應 （最近鄰或帶距離閾值的匹配策略）。
• 對每對對應 構造協方差和權重：
  
• 構造代價函數（總和）：
  
• 對 在當前
• 求解線性系統，更新 ，迭代直至收斂或達最大迭代次數。

4. 輸出：估計的剛性變換 。

---

6. 核心方法細節

6.1 標準ICP算法

標準 ICP 算法的關鍵思想可以總結為兩個步驟：

1. 計算兩次掃描之間的對應點。
2. 計算一個剛體變換，使對應點之間的距離最小化。

迭代重複這兩個步驟通常會收斂到期望的變換結果。由於違反了完全重疊 (full overlap) 的假設，因此必須引入一個最大匹配閾值 。該閾值用於處理某些點在第二幅掃描中沒有對應點的情況（例如那些位於掃描 A 邊界之外的點）。

在大多數 ICP 的實現中，

• 取值過小會導致收斂性差（算法“短視”）；
• 取值過大會導致錯誤的對應關係將最終配準結果拉離正確解。

標準 ICP 如算法 1 所示。

---

算法 1：標準 ICP

輸入：

• 兩個點雲：
• 初始變換：

輸出：

• 正確的變換 ，用於對齊點雲 與

---

6.2 Point-to-Plane ICP算法

點到平面變體的 ICP 利用表面法向信息來提升配準性能。該方法最初由 Chen 和 Medioni 提出，在處理 2.5D 深度數據時，已經成為一種比標準 ICP 更穩健、更精確的變體。

與最小化 的點到點方法不同，點到平面算法最小化的是沿表面法線方向的誤差（即 在由表面法線張成的子空間上的投影）。

這一改進可以通過修改算法 1 的第 11 行來實現，如下所示：

其中 是點 處的表面法線。

---

6.3 Generalized-ICP算法

Generalized-ICP 的核心思想是在算法 1 的第 11 行最小化步驟中引入 概率模型，而算法的其他部分保持不變。這一設計在降低複雜度的同時維持了計算速度。需要注意的是：點對的對應關係依然通過標準歐幾里得距離來確定，而不是基於概率度量。這麼做的好處是仍能利用 kd-tree 進行最近鄰搜索，從而保持 ICP 相比全概率方法的主要優勢——速度與簡潔性。

由於只有第 11 行涉及推導，下面將範圍限定在該上下文。假設最近點查找已完成，並且兩個點雲

已根據對應關係索引（即 與

的對應點均已被移除。

---

概率模型

假設存在一組潛在點集：

它們生成觀測點集 與 ，即：

其中

若假設 完美對應關係（幾何上一致，無遮擋或採樣誤差），並且存在正確的剛體變換 ，則有：

對於任意剛體變換 ，定義：

考慮 的分佈：由於 與

結合式 (1)，化簡為：

---

最大似然估計

通過最大似然估計（MLE），迭代求解 ：

進一步簡化為：

這就是 Generalized-ICP 的關鍵步驟。

---

與標準 ICP 的關係

標準 ICP 是式 (2) 的特例。若取

則式 (2) 化簡為：

正是標準 ICP 的更新公式。

---

與點到平面 ICP 的關係

點到平面 ICP 的更新步驟為：

其中 為投影矩陣，投影到 點的法向所張成的子空間上。由於

因此：

從而式 (4) 可改寫為：

對比式 (5) 與式 (2)，可得點到平面 ICP 是 Generalized-ICP 的極限情況，此時：

嚴格來説 不可逆，但若用可逆矩陣 近似，當

直觀理解為：點

---

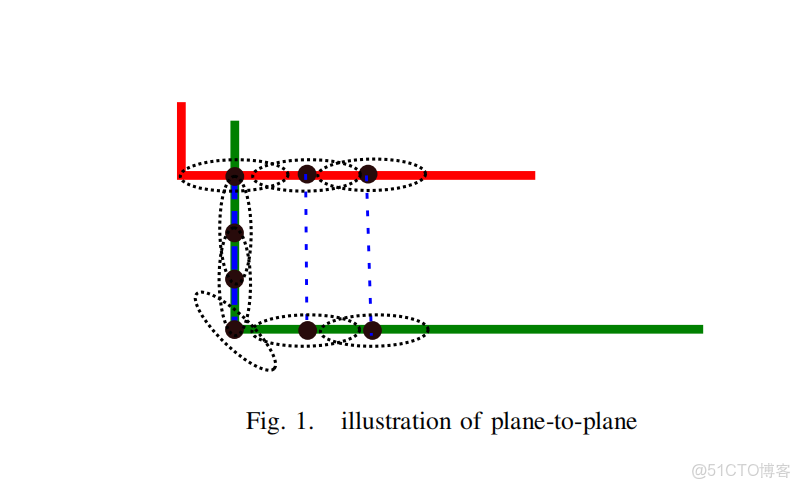
應用：面到面 (plane-to-plane)

為了優於點到平面方法並增強對稱性，Generalized-ICP 可擴展為 同時利用兩個點雲的表面信息。最直接的方法是將

---

基本思想

點雲本質上是三維表面的採樣，而非任意點集。局部表面近似為平面，因此每個採樣點僅在 表面法向方向提供約束。

• 法向方向：協方差很小（約束強）；
• 切平面方向：協方差很大（約束弱）。

設某點法向為 ，其協方差矩陣為：

其中

---

協方差矩陣構造

設 的法向為 ， 的法向為 ，則：

最終變換

---

魯棒性與直觀解釋

在極端情況下（如綠色點雲的垂直部分錯誤匹配到紅色點雲同一點），由於法向不一致，plane-to-plane 會自動降低這些錯誤匹配的權重。其對應協方差矩陣趨於各向同性，在目標函數中的貢獻極小。換言之，這是 軟約束：紅點沿 x 自由，綠點沿 y 自由，因此這些錯誤匹配幾乎不會影響整體配準。

---

法向量估計

構造表面協方差矩陣需要為兩點雲估計法向量。方法很多，常見的是 PCA：對每點取最近 20 個鄰居，計算協方差矩陣並分解，其最小特徵值對應的特徵向量即為該點的法向。此法在點到平面 ICP 與 Generalized-ICP 中均可使用。
在 Generalized-ICP 中，進一步構造旋轉矩陣，將

---

7. 算法優勢與侷限

優勢

• 更合理的誤差面：利用兩側局部幾何信息，代價更接近二次、收斂性更好。常在含平面和噪聲的場景中表現穩定。
• 統一框架：可視為點到點與點到面 ICP 的泛化；靈活調節協方差可在不同情形下切換行為。
• 對密度差/採樣不均衡更魯棒：因為協方差能反映局部採樣結構與不確定性。

侷限 / 注意點

• 計算開銷：需為每點計算協方差（kNN 搜索 + SVD/特徵分解或直接樣本協方差），以及每對匹配中求逆 S（3×3，雖小但仍有開銷）；整體比純點到點 ICP 更慢。實現須做優化（近鄰加速、緩存協方差、並行、對 S 做快速求逆等）。
• 對不良匹配仍敏感：如果對應關係錯誤（大位移或遮擋造成的錯誤最近鄰），馬氏代價會懲罰但不能完全避免錯誤配對影響；仍需使用重投票、距離閾值或魯棒損失（Huber、Tukey）等方法。
• 退化情形：在完全結構化的平面或柱面等退化幾何下，協方差可能是奇異的（需正則化）；某些場景仍會遇到可觀測性問題。

---

8. 實踐建議

• 協方差估計：k 的選擇（典型 10–30）影響平滑與局部敏感性；對稀疏或含外點的點雲要小心。對噪聲高的掃描可在協方差上加。
• 預處理：計算法線 / 協方差時先做下采樣（voxel grid）可以顯著加速且往往對結果無害（甚至更好）。
• 加權 / 魯棒化：在求解線性系統時可在代價上再加魯棒核以降低錯誤對應影響。
• 初始變換：GICP 比點到點更魯棒，但仍需要一定的初始值（畸變很大時會卡在局部）。可用特徵匹配或粗配準先驗。
• 高效實現要點：緩存協方差、並行化協方差計算與最近鄰搜索、對 S 做 Cholesky 預分解以快速求解。很多開源實現（PCL 的 GICP）已有這些優化。

---

9. 參考實現與擴展

• PCL（Point Cloud Library） 中有 GICP 的實現（pcl::GeneralizedIterativeClosestPoint），並對性能做了工程優化；可以直接參考或調用。很多 SLAM/LOAM 工程在點雲配準環節採用了 PCL-GICP 或其變體。
• 各種擴展：Multi-Channel GICP（處理強度/顏色通道）、視覺引導的 GICP、以及在點雲分片/多尺度上的改進。最新工作多關注加速、魯棒性和退化檢測。

---

10. 關鍵公式

• 局部協方差：
  
• 誤差：
  
• 融合協方差：
  
• 加權代價：
  
• 線性系統：
  

---

11. 結論

GICP 用局部協方差 + 馬氏距離的概率框架整合了點到點與點到面的思想，在多數帶平面結構或噪聲/密度差異的現實點雲中表現更穩健，是工業與學術界點雲配準的常用基線；其代價在準確性和魯棒性上通常優於經典 ICP，但代價是更高的計算開銷與實現複雜度。

---

12. 參考文獻

• A. V. Segal, D. Haehnel, S. Thrun, “Generalized-ICP”, Robotics: Science and Systems (RSS), 2009.
• PCL 文檔和 pcl::GeneralizedIterativeClosestPoint 源碼（工業實現與優化）。

---