文章目錄
- 前言
- 一、現如今的”Transformer“
- 二、Attention Serious
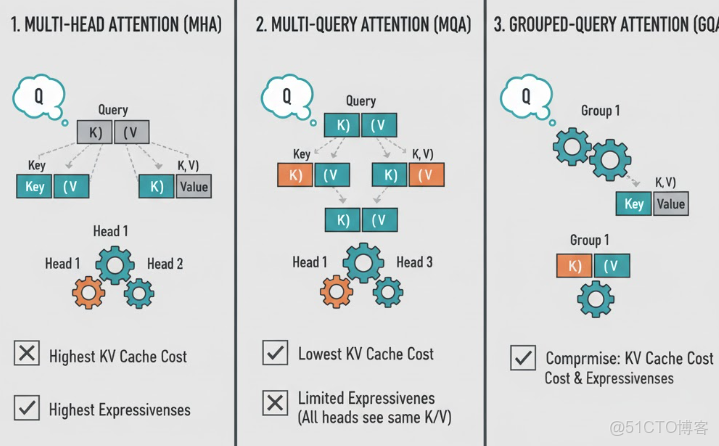
- 2.1 Multi-Head Attention (MHA)
- 2.2 Multi-Query Attention (MQA)
- 2.3 Grouped Query Attention (GQA)
- 三、歸一化:LayerNorm → RMSNorm + Pre-Norm
- 🔹 Post-Norm(原始 Transformer 用法)
- 🔹 Pre-Norm(現代 LLM 常用)
- 3.1 LayerNorm
- 🧠 1.為什麼不用 BatchNorm,而用 LayerNorm / RMSNorm?(面經)
- 3.2 RMSNorm
- 四、總結
前言
✍ 在大模型論文學習中,相信很多讀者和筆者一樣,一開始都會有一種感覺:“現在大模型架構都差不多,主要是數據和算力在堆積。”當筆者慢慢總結LLaMA、Qwen、DeepSeek這些模型架構的時候發現,在 Attention、位置編碼、FFN 與歸一化 上,其實已經悄悄從經典 Transformer 走到了另一套“默認配置”。相較於最初的 Transformer,現在的主流大模型在架構上,已經逐漸從:
- MQA → GQA(Grouped Query Attention)
- 絕對位置編碼 → RoPE(Rotary Positional Embedding)
- ReLU / GELU 前饋網絡 → SwiGLU 前饋網絡
- LayerNorm → RMSNorm + Pre-Norm
- …
因此,在本文的學習中,我們主要聚焦於目前的大模型”默認配置“的學習,瞭解現在的”Transformer“!
一、現如今的”Transformer“
讀者肯定很疑惑,為什麼我要把第一章名字起為現如今的”Transformer“,實際上在以前,不管是科研還是工作,大家都會把Transformer作為一個baseline去進行優化,就像BERT、GPT等等,一直沿用的是Transformer的架構。但到了現在,研究者發現其中模塊的更替可以達到更好的的效果。因此,現如今的大模型,已經不再直接將以前的Transformer架構作為baseline,而是將更換了模塊的Transformer架構作為baseline。那現如今的baseline模塊長什麼樣子呢,筆者統計了比較經典的模塊所採用的注意力機制、位置編碼、MLP激活層以及歸一化的方式:
|
模型家族
|
注意力
|
位置編碼
|
MLP 激活
|
歸一化
|
|
早期 GPT/BERT
|
MHA
|
絕對 PE / learned pos
|
GELU
|
LayerNorm
|
|
LLaMA 1/2/3 系列 |
GQA(大模型)
|
RoPE
|
SwiGLU
|
RMSNorm
|
|
Qwen2 / Qwen2.5 |
GQA
|
RoPE
|
SwiGLU
|
RMSNorm
|
|
Mistral 7B |
GQA + sliding window
|
RoPE
|
SwiGLU
|
RMSNorm
|
|
DeepSeek-LLM 等 |
GQA/自研高效注意力
|
RoPE
|
SwiGLU
|
RMSNorm
|
|
Granite / Gemma 等 |
GQA/MQA
|
RoPE
|
SwiGLU/GeGLU
|
RMSNorm/LN
|
如表格所示, 對比早期 GPT/BERT 模型我們就可以發現了,現如今大模型的各個模塊都有所改變:
- 注意力機制:MQA → GQA(Grouped Query Attention)
- 位置編碼: 絕對位置編碼 → RoPE(Rotary Positional Embedding)
- MLP 激活層:ReLU / GELU 前饋網絡 → SwiGLU 前饋網絡
- 歸一化: LayerNorm → RMSNorm + Pre-Norm
所以如果你能把這四件套講明白,基本就把現代 LLM 架構裏 理清,並且可以快速找到文章的貢獻點。
二、Attention Serious
2.1 Multi-Head Attention (MHA)
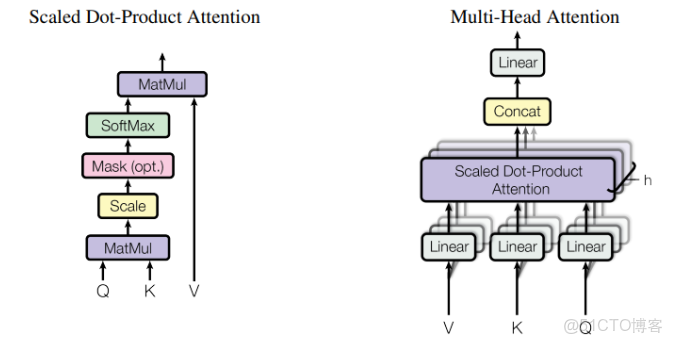
首先來回顧一下以前的注意力機制:

在標準的自注意力中,我們通過
將輸入特徵通過不同的線性投影矩陣,映射到多個低維子空間中:

然後將所有頭拼接(concatenate)再線性變換:
MHA通過多個小頭可以從不同角度捕捉語義信息,增強模型的表達能力和穩定性,比單頭更魯棒。
- 代碼手撕
import torch
import torch.nn as nn
import torch.nn.functional as F
class MultiHeadAttention(nn.Module):
def __init__(self, d_model, num_heads, dropout=0.0):
super().__init__()
assert d_model % num_heads == 0
self.d_model = d_model
self.num_heads = num_heads
self.head_dim = d_model // num_heads
self.w_q = nn.Linear(d_model, d_model)
self.w_k = nn.Linear(d_model, d_model)
self.w_v = nn.Linear(d_model, d_model)
self.w_o = nn.Linear(d_model, d_model)
self.dropout = nn.Dropout(dropout)
def forward(self, x, attn_mask=None):
"""
x: [B, L, d_model]
"""
B, L, _ = x.size()
# 1. 線性投影
Q = self.w_q(x) # [B, L, d_model]
K = self.w_k(x)
V = self.w_v(x)
# 2. reshape 為 [B, H, L, Dh]
def reshape_heads(t):
return t.view(B, L, self.num_heads, self.head_dim).transpose(1, 2)
Q = reshape_heads(Q)
K = reshape_heads(K)
V = reshape_heads(V)
# Q,K,V: [B, H, L, Dh]
# 3. 縮放點積注意力
scores = Q @ K.transpose(-2, -1) / (self.head_dim ** 0.5) # [B, H, L, L]
if attn_mask is not None:
scores = scores.masked_fill(attn_mask == 0, float('-inf'))
attn = F.softmax(scores, dim=-1)
attn = self.dropout(attn)
out = attn @ V # [B, H, L, Dh]
# 4. 合併頭
out = out.transpose(1, 2).contiguous().view(B, L, self.d_model)
return self.w_o(out)2.2 Multi-Query Attention (MQA)
有了 MHA 之後,大家第一反應是:頭越多越好,越能學到多種語義關係。但在大模型、尤其是 Decoder-Only + 長上下文 + 自迴歸生成 的場景下,MHA 暴露出了一個非常現實的問題:
KV Cache 太貴了。
在自迴歸生成過程中,每生成一個新 token,都需要用到歷史所有位置的
- 對於標準 MHA:每個注意力頭都維護一份自己的
- 如果有
個頭,那麼 KV Cache 的內存開銷大致是:
當我們把頭數堆到 32、64 甚至更多,再把上下文長度拉到 32K、64K 時,這個開銷就會變成顯存吞噬怪,直接限制推理速度與可部署性。因此,為了在幾乎不損失模型效果的前提下,壓縮 KV Cache 和帶寬成本,就提出了 Multi-Query Attention(MQA)。
MHA中的每一個頭都是獨享一份
MQA 提出了所有的頭共享同一份

於是每個頭的注意力就變成:

最後依然是拼接再線性變換:

💡 經驗發現“多 KV”並沒有帶來線性收益, Q 仍然是多頭的,多頭仍能捕捉多種語義關係。
- 代碼手撕
class MultiQueryAttention(nn.Module):
def __init__(self, d_model, num_heads, dropout=0.0):
super().__init__()
assert d_model % num_heads == 0
self.d_model = d_model
self.num_heads = num_heads
self.head_dim = d_model // num_heads
self.w_q = nn.Linear(d_model, d_model)
# 注意:K/V 只有一組,所以輸出維度是 head_dim
self.w_k = nn.Linear(d_model, self.head_dim)
self.w_v = nn.Linear(d_model, self.head_dim)
self.w_o = nn.Linear(d_model, d_model)
self.dropout = nn.Dropout(dropout)
def forward(self, x, attn_mask=None):
"""
x: [B, L, d_model]
"""
B, L, _ = x.size()
# 1. 多頭 Q
Q = self.w_q(x) # [B, L, d_model]
Q = Q.view(B, L, self.num_heads, self.head_dim).transpose(1, 2)
# Q: [B, H, L, Dh]
# 2. 單頭 K/V
K = self.w_k(x) # [B, L, Dh]
V = self.w_v(x) # [B, L, Dh]
# 3. 為了和 Q 匹配,將 K/V 在頭維上 broadcast
K = K.unsqueeze(1) # [B, 1, L, Dh]
V = V.unsqueeze(1) # [B, 1, L, Dh]
K = K.expand(B, self.num_heads, L, self.head_dim)
V = V.expand(B, self.num_heads, L, self.head_dim)
# 4. 縮放點積注意力(與 MHA 相同)
scores = Q @ K.transpose(-2, -1) / (self.head_dim ** 0.5) # [B, H, L, L]
if attn_mask is not None:
scores = scores.masked_fill(attn_mask == 0, float('-inf'))
attn = F.softmax(scores, dim=-1)
attn = self.dropout(attn)
out = attn @ V # [B, H, L, Dh]
out = out.transpose(1, 2).contiguous().view(B, L, self.d_model)
return self.w_o(out)2.3 Grouped Query Attention (GQA)
根據前面兩節的分析,我們可以總結出:
- MHA:每個頭都有獨立的
,表達能力強,但 KV Cache 成本最高;
- MQA:所有頭共享同一份
,KV Cache 成本最低,但多頭之間視角差異弱,表達能力稍打折
於是就自然出現了一個折中思路:能不能在 “省 KV” 和 “頭之間有點差異” 之間找個平衡?這就是 Grouped-Query Attention(GQA)。GQA 的核心思想:Q 仍然是很多頭,但 K/V 的頭數減少為更少的組(num_kv_heads),每組 KV 服務若干個 Q 頭。
- 代碼手撕
class GroupedQueryAttention(nn.Module):
def __init__(self, d_model, num_q_heads, num_kv_heads, dropout=0.0):
super().__init__()
assert d_model % num_q_heads == 0
assert num_q_heads % num_kv_heads == 0
self.d_model = d_model
self.num_q_heads = num_q_heads
self.num_kv_heads = num_kv_heads
self.head_dim = d_model // num_q_heads
self.group_size = num_q_heads // num_kv_heads # 每組多少個 Q 頭共享一個 KV
self.w_q = nn.Linear(d_model, d_model)
self.w_k = nn.Linear(d_model, num_kv_heads * self.head_dim)
self.w_v = nn.Linear(d_model, num_kv_heads * self.head_dim)
self.w_o = nn.Linear(d_model, d_model)
self.dropout = nn.Dropout(dropout)
def forward(self, x, attn_mask=None):
"""
x: [B, L, d_model]
"""
B, L, _ = x.size()
# 1. Q: 多頭; K/V: 少量頭
Q = self.w_q(x) # [B, L, d_model]
K = self.w_k(x) # [B, L, num_kv_heads * head_dim]
V = self.w_v(x)
Q = Q.view(B, L, self.num_q_heads, self.head_dim).transpose(1, 2)
K = K.view(B, L, self.num_kv_heads, self.head_dim).transpose(1, 2)
V = V.view(B, L, self.num_kv_heads, self.head_dim).transpose(1, 2)
# Q: [B, Hq, L, Dh]
# K,V: [B, Hkv, L, Dh]
# 2. 將每個 KV 頭“擴展”為 group_size 個 Q 頭使用
# 例如 Hq=8, Hkv=2 -> group_size=4
K = K.repeat_interleave(self.group_size, dim=1) # [B, Hq, L, Dh]
V = V.repeat_interleave(self.group_size, dim=1)
# 3. 縮放點積注意力
scores = Q @ K.transpose(-2, -1) / (self.head_dim ** 0.5) # [B, Hq, L, L]
if attn_mask is not None:
scores = scores.masked_fill(attn_mask == 0, float("-inf"))
attn = F.softmax(scores, dim=-1)
attn = self.dropout(attn)
out = attn @ V # [B, Hq, L, Dh]
# 4. 合併頭
out = out.transpose(1, 2).contiguous().view(B, L, self.d_model)
return self.w_o(out)三、歸一化:LayerNorm → RMSNorm + Pre-Norm
在 Transformer 裏,歸一化(Normalization)主要解決兩個問題:
- 深層網絡訓練不穩定:梯度可能爆炸或消失;
- 不同層輸出分佈漂移,導致學習變慢。
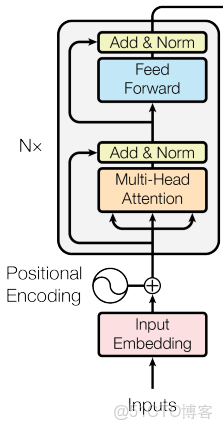
最早的 Transformer 使用的是 LayerNorm + Post-Norm 殘差結構(指在全連接層後跟上一個歸一化層)
但到了 LLaMA、DeepSeek 等大模型時,大家開始逐漸轉向:RMSNorm + Pre-Norm(指在全連接層前跟上一個歸一化層)
🔹 Post-Norm(原始 Transformer 用法)
最早的 Transformer 論文(Attention Is All You Need)使用的是 Post-Norm,代碼結構類似:
# Post-Norm 結構
out = x + sublayer(x)
out = layer_norm(out)🔹 Pre-Norm(現代 LLM 常用)
大多數現代 LLM(如 LLaMA、DeepSeek 系列)改成了 Pre-Norm:代碼結構類似:
# Pre-Norm 結構
h = layer_norm(x)
out = x + sublayer(h)💡 實踐上,Pre-Norm 再配合 RMSNorm,只調節尺度不改均值,在 Decoder-only 結構裏訓練更穩定、實現也更簡單。
3.1 LayerNorm
Layer Normalization(LN)是在 Transformer 中使用最廣的歸一化方式之一。給定一個 token 的隱藏表示 
其中:
是可學習的縮放和平移參數;
- 歸一化是在單個樣本、單個 token 的通道維度上完成的。
🧠 直覺理解:
對每個 token 的特徵做一遍“標準化 + 線性變換”,
讓每一層看到的分佈更平滑,避免某些維度過大/過小導致訓練不穩。
在 PyTorch 中,你平時看到的 nn.LayerNorm 就是這個東西:
import torch
import torch.nn as nn
x = torch.randn(2, 4, 8) # [B, L, d_model]
ln = nn.LayerNorm(8)
y = ln(x) # 每個位置的最後一維做 LN🧠 1.為什麼不用 BatchNorm,而用 LayerNorm / RMSNorm?(面經)
這一問是面試官很喜歡的一個考點,尤其是 Transformer / LLM 崗位。核心區別在於:歸一化時用哪些維度來統計均值與方差。
- BatchNorm(BN):
- 在 CV 裏常用,對 batch 維度 + 空間維度 做統計;
- 對每個通道c,使用整批數據的統計量:
- LayerNorm(LN):
- 對單個樣本、單個 token 的所有特徵求均值和方差,不依賴 batch 大小。
在 Transformer / LLM 場景中,BN 存在幾個問題:
- 序列長度不固定:BN 在變長序列上不自然,統計維度不好選;
- 推理階段 batch 很小甚至為 1:BN 的 running mean/var 與訓練時差異大,容易分佈漂移;
- 自注意力中不同 token 之間差異大:BN 混合不同 token 的統計量,會引入額外噪聲。
因此,大模型裏更偏向用 LayerNorm / RMSNorm 這種“不依賴 batch、只看自己”的歸一化方式。
3.2 RMSNorm
RMSNorm 是基於“層歸一化中主要起作用的是縮放因子,而非平移因子”這個發現而提出的歸一化方法。在層歸一化中需要減去均值,而模型在訓練過程中已經學會通過投影矩陣自動調節均值;而 

🧠 直覺理解:
RMSNorm 更像是“把這個向量整體縮放到一個合適能量水平”,
不去把它“拉回 0 均值”,只控制它的尺度。
💡 實踐上,在 Decoder-only 大模型裏:RMSNorm + Pre-Norm 組合在超深層網絡(幾十層)上表現更穩定,這也是 LLaMA / DeepSeek / Qwen 等系列廣泛採用它的原因之一。
- 代碼手撕
class RMSNorm(nn.Module):
def __init__(self, d_model, eps=1e-8):
super().__init__()
self.weight = nn.Parameter(torch.ones(d_model))
self.eps = eps
def forward(self, x):
"""
x: [B, L, d_model]
"""
# 均方根:sqrt(mean(x^2))
rms = x.pow(2).mean(dim=-1, keepdim=True).add(self.eps).sqrt()
x_norm = x / rms
return self.weight * x_norm四、總結
本章我們先把現代大模型裏的兩塊“基礎設施”打牢:一塊是從 MHA → MQA → GQA 的注意力演化,用更少的 KV 頭(甚至共享 KV)在不明顯掉點的前提下,大幅降低 KV Cache 與長上下文顯存開銷;另一塊是從 LayerNorm → RMSNorm + Pre-Norm 的歸一化升級,用“只歸一化能量”的 RMSNorm 配合 Pre-Norm 結構,讓超深的 Decoder-only 模型在訓練和推理中都更加穩定。後面的章節,我們再把 RoPE / SwiGLU / MoE / MLA 這些“進階武器”一個個拆開,拼成一整套現代 LLM 的“架構面經圖譜”。