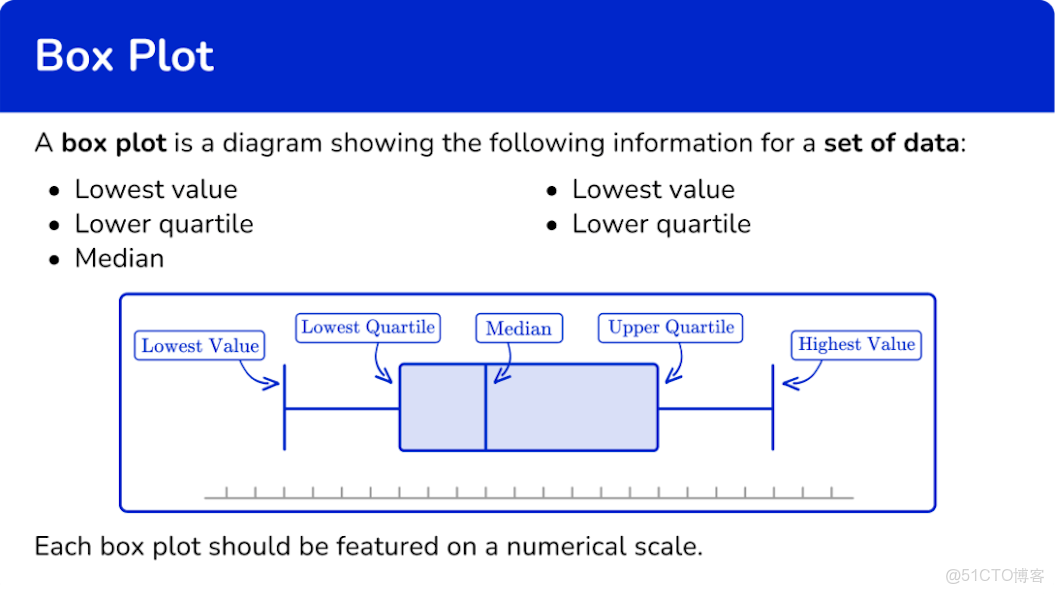
箱型圖法則是數據處理領域中用於識別異常值(outliers)的經典統計方法,其核心邏輯基於信息的四分位數(quartile)分佈特徵,藉助量化數據的離散程度來界定正常信息與異常值的邊界,具有客觀、高效且易操控的特點,被廣泛應用於數據分析、質量控制、金融風控等多個領域。
一、關鍵統計指標
箱型圖法則的應用首先需明確兩個關鍵統計指標——四分位數,即下四分位數(First Quartile, Q1)和上四分位數(Third Quartile, Q3)。在有序排列的數據集中,Q1代表處於25%分位的內容值,意味着有25%的數據小於該值;Q3則代表處於75%分位的材料值,即有75%的信息小於該值。通過這兩個分位數,可進一步計算出反映數據中間50%核心分佈範圍的指標——四分位距(Interquartile Range, IQR),其計算公式為IQR = Q3 - Q1。IQR的值越大,説明數據中間50%的分佈越分散,反之則越集中。
箱型圖法則的核心環節。基於四分位距的特性,該法則設定了明確的異常值判定標準:當某一內容點的數值小於Q1 - 1.5IQR,或大於Q3 + 1.5IQR時,該數據點即被判定為異常值。這一判定邊界的設定,既能夠有效捕捉到顯著偏離數據整體分佈的極端值,又能最大程度避免將正常的隨機波動素材誤判為異常,完成了異常值識別的精準性與魯棒性的平衡。就是異常值的判定
箱型圖法則的價值不僅體現在理論層面,更在實際場景中展現出強大的應用能力,以下將結合兩個典型案例具體説明。
二、案例一:電商平台日銷售額異常值識別
某電商平台收集了30天的日銷售額材料(單位:萬元),為精準分析銷售趨勢,需先經過箱型圖法則識別異常值。首先對30天數據按從小到大排序,計算得出Q1=52、Q3=88,由此可得IQR=88-52=36。根據判定標準,異常值邊界為Q1-1.5IQR=52-1.5×36=2,Q3+1.5IQR=88+1.5×36=142。
梳理數據後發現,有兩天數據超出邊界:一天因系統故障導致銷售額僅1萬元(小於2萬元),另一天因大型促銷活動銷售額達150萬元(大於142萬元)。這兩個數據點均被判定為異常值。考慮到素材的連續性需求,平台未直接刪除異常值,而是採用線性插值法補全。對於1萬元的異常值,其前後相鄰有效數據為3萬元(第5天)和5萬元(第7天),按公式計算補全值為4萬元;對於150萬元的異常值,前後有效數據為90萬元(第22天)和85萬元(第24天),補全值為87.5萬元。補全後的數據更貼合日常銷售趨勢,為後續的庫存規劃、營銷方案制定供應了可靠依據。
三、案例二:工業產品尺寸質量檢測
某機械加工廠生產一批零件,需對其直徑尺寸(單位:mm)進行質量檢測,抽取50個零件的尺寸數據後,運用箱型圖法則篩選異常值。經計算,內容的Q1=19.8、Q3=20.2,IQR=20.2-19.8=0.4,異常值邊界為19.8-1.5×0.4=19.2,20.2+1.5×0.4=20.8。
檢測發現有3個零件尺寸異常,分別為19.0mm、21.0mm、19.1mm,這些異常值可能是由機牀精度波動、測量誤差等原因導致。由於零件尺寸素材對生產調整至關重要,工廠採用線性插值法對異常值進行修正。以19.0mm的異常值為例,其前後合格零件尺寸為19.7mm(第18個)和19.9mm(第20個),計算得補全值為19.8mm。修正後的尺寸資料準確反映了零件生產的整體狀態,幫助技術人員及時調整機牀參數,降低了後續生產的不合格率。
四、案例三:智能鞋墊運動數據異常值處理
智能硬件公司研發的運動鞋墊,可實時採集用户跑步時的足底壓力信息(單位:kPa),用於分析運動姿態與運動損傷風險。某用户連續佩戴鞋墊跑步30分鐘,系統每1秒採集1組數據,共獲得1800組壓力數據,需通過箱型圖法則處理數據中的異常值。
首先對1800組信息進行排序與統計,計算得出足底壓力數據的Q1=125kPa、Q3=210kPa,因此四分位距IQR=210-125=85kPa。根據箱型圖法則的異常值判定標準,計算得到異常值邊界:下限為Q1-1.5IQR=125-1.5×85=0.5kPa,上限為Q3+1.5IQR=210+1.5×85=337.5kPa。
內容篩選後發現兩類異常值:一類是壓力值為0kPa的12組數據(小於0.5kPa),經排查為鞋墊與手機藍牙短暫斷連導致的信息缺失;另一類是壓力值達350kPa的8組數據(大於337.5kPa),源於用户跑步時偶然踩入小坑導致的瞬時壓力突變。由於這些異常值會干擾運動姿態分析的準確性,且數據具有明顯的時間序列特徵,採用線性插值法進行補全。
以第150秒的異常值(0kPa)為例,其前後相鄰的有效信息為第149秒的130kPa和第151秒的135kPa,代入線性插值公式計算補全值:y=130 + (150-149)×(135-130)/(151-149)=132.5kPa。對於第220秒的350kPa異常值,前後有效材料為第219秒的205kPa和第221秒的212kPa,補全值為208.5kPa。補全後的壓力內容完整呈現了用户跑步過程中足底壓力的變化曲線,為後續的落地姿態優化建議提供了精準的數據支撐。
從上述案例可見,箱型圖法則藉助“四分位數定義範圍—四分位距量化離散度—邊界閾值判定異常”的完整邏輯鏈條,為異常值識別提供了標準化方案。同時,結合科學的異常值處理方法,既能剔除數據“噪聲”,又能保證數據完整性,是數據預處理環節中不可或缺的關鍵設備。
五、常用開源函數庫及基礎應用
在實際數據處理中,無需手動編寫艱難計算邏輯,主流編程語言的開源函數庫已封裝好箱型圖法則的核心功能,以下為兩類常用庫的介紹及基礎使用示例。
1.Python 生態:Pandas 與 Matplotlib/Seaborn
Python 作為數據分析主流語言,Pandas 庫提供了四分位數計算與異常值篩選的便捷接口,Matplotlib 或 Seaborn 可用於可視化箱型圖直觀呈現異常值。
基礎使用步驟:第一通過 Pandas 讀取數據並計算四分位數與四分位距,之後依據箱型圖法則判定異常值,最後結合 Matplotlib 繪製箱型圖。示例代碼邏輯如下:
import pandas as pd
import matplotlib.pyplot as plt
構造示例數據(模擬電商日銷售額)
data = pd.Series([52, 60, 75, 88, 1, 150, 68, 72, 80])
計算四分位數
Q1 = data.quantile(0.25)
Q3 = data.quantile(0.75)
IQR = Q3 - Q1
定義異常值邊界
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR
篩選異常值
outliers = data[(data < lower_bound) | (data > upper_bound)]
print(“異常值:”, outliers.values)
繪製箱型圖(直觀展示異常值)
plt.boxplot(data, vert=False, patch_artist=True)
plt.xlabel(“日銷售額(萬元)”)
plt.title(“電商平台日銷售額箱型圖(含異常值標記)”)
plt.show()
上述代碼中,Pandas 的 quantile() 技巧可快速計算四分位數,通過簡單邏輯即可篩選異常值,Matplotlib 的 boxplot() 函數會自動在圖中標記出異常值(以圓點形式呈現)。
2.R 語言生態:dplyr 與 ggplot2
R 語言在統計分析領域應用廣泛,dplyr 庫可高效處理數據計算,ggplot2 庫則擅長繪製專業的箱型圖。
基礎使用示例:利用 dplyr 計算統計量,結合 ggplot2 可視化異常值,代碼邏輯如下:
library(dplyr)
library(ggplot2)
構造示例素材
data <- data.frame(銷售額 = c(52, 60, 75, 88, 1, 150, 68, 72, 80))
計算四分位數與異常值邊界
stats <- data %>%
summarize(Q1 = quantile(銷售額, 0.25),
Q3 = quantile(銷售額, 0.75),
IQR = Q3 - Q1,
lower_bound = Q1 - 1.5 * IQR,
upper_bound = Q3 + 1.5 * IQR)
篩選異常值
outliers <- data %>%
filter(銷售額 < stats
print(outliers)
繪製箱型圖
ggplot(data, aes(y = 銷售額)) +
geom_boxplot(fill = “lightblue”) +
labs(y = “日銷售額(萬元)”, title = “電商平台日銷售額箱型圖”) +
theme_minimal()
這些開源函數庫的優勢在於將箱型圖法則的底層邏輯封裝,使用者無需關注複雜的計算細節,只需調用相關接口即可快速完成異常值的識別與可視化,極大提升了數據處理效率。無論是Python還是R語言的庫,都支持結合線性插值等方法進行異常值補全,可根據實際使用的編程語言生態靈活選擇。