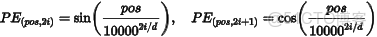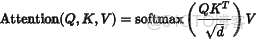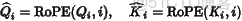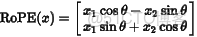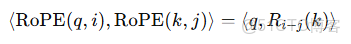簡介

RoPE（Rotary Positional Embedding）是當前大語言模型中最主流的位置編碼方式，通過旋轉矩陣操作將位置信息引入Q、K向量角度，實現相對位置建模。它支持長序列泛化、計算高效且保留週期信息，被LLaMA、GPT-NeoX等主流大模型採用。相比傳統位置編碼，RoPE能更好地處理序列順序信息，提升模型對相對距離的感知能力。

在 Transformer 架構中，位置編碼（Position Encoding）是理解序列順序的關鍵機制。自從 Google 提出原始的 Sinusoidal 編碼以來，研究者一直在探索更高效、可泛化的方式。RoPE（Rotary Positional Embedding） 就是在這一背景下被提出的，它已被廣泛應用於大模型如 LLaMA、GPT-NeoX、Grok、ChatGLM 等，是現代 LLM 架構的標準配置。

希望大家帶着下面的問題來學習，我會在文末給出答案。

·RoPE 明明是“位置編碼”，為什麼不直接加在 embedding 上，而是要“旋轉”查詢和鍵向量？

·RoPE 如何實現相對位置建模？它是怎麼讓注意力知道“距離”的？

·RoPE 的“旋轉矩陣”會不會破壞向量的語義信息？這種操作真的合理嗎？

一、為什麼需要位置編碼？

Transformer 本身不具備序列感知能力，因為它的結構是並行的、多頭注意力機制，並沒有天然的順序意識。

所以必須引入某種“位置信息”來幫助模型區分第1個 token 和第10個 token。

二、傳統的兩種位置編碼方式

1. 絕對位置編碼（Absolute PE）

最早的 Sinusoidal Encoding（如在原始 Transformer 中）使用如下公式：

優點：無需學習，固定函數缺點：絕對編碼，無法處理變化的上下文窗口或相對關係。

2. 可學習位置向量（Learned PE）

直接給每個位置一個可學習向量 pos_embedding[position]，缺點是固定長度，不能泛化到更長序列。

三、RoPE 是什麼？

RoPE（Rotary Position Embedding），由 Su et al. 在論文《RoFormer: Enhanced Transformer with Rotary Position Embedding》中提出，核心思想是：

“不是將位置編碼與 token embedding 相加，而是通過一個旋轉矩陣操作，將位置信息引入 Q、K 向量的角度中。”

用直觀的話説，就是：

·將位置編碼看作一個二維旋轉角度

·讓 QK 的 dot-product 計算本身隱含序列順序差異

·因為旋轉可以表示相對位置，所以天然支持 相對位置感知

四、RoPE 的數學原理

我們先看 Transformer 中注意力的核心：

在 RoPE 中，我們不是單純使用 Q 和 K，而是將它們進行位置旋轉處理：

其中的旋轉操作可以理解為將向量每對兩個維度旋轉一個角度，角度由位置 index 決定。例如在二維空間：

整個向量通過旋轉矩陣變換，就帶有了與位置相關的角度偏移。

五、 RoPE 的 Python 實現

import numpy as np
import matplotlib.pyplot as plt
def get_positional_encoding(seq_len, d_model):
pos = np.arange(seq_len)[:, np.newaxis]
i = np.arange(d_model)[np.newaxis, :]
angle_rates = 1 / np.power(10000, (2 * (i // 2)) / np.float32(d_model))
angle_rads = pos * angle_rates
# apply sin to even indices, cos to odd indices
pos_encoding = np.zeros_like(angle_rads)
pos_encoding[:, 0::2] = np.sin(angle_rads[:, 0::2])
pos_encoding[:, 1::2] = np.cos(angle_rads[:, 1::2])
return pos_encoding
# visualize
pe = get_positional_encoding(100, 16)
plt.figure(figsize=(12, 6))
plt.plot(pe[:, :8])
plt.legend([f"dim {i}" for i in range(8)])
plt.title("Positional Encoding (first 8 dimensions)")
plt.xlabel("Position")
plt.ylabel("Value")
plt.grid(True)
plt.show()

這個過程在 GPT-NeoX、LLaMA 中會集成在 rotary_embedding 層中。

六、RoPE 的優點總結

七、哪些模型使用了 RoPE？

·LLaMA 系列（1~3）：大規模開源模型都使用 RoPE

·Grok-1（xAI）：採用 RoPE + MoE 架構

·GPT-NeoX：引入 RoPE 替代原始位置編碼

·ChatGLM 系列：國產 LLM 中廣泛採用

·Baichuan, InternLM, Qwen 等：國產大模型通用配置

八、總結

RoPE 是當前大語言模型中最實用、最主流的序列位置編碼方式之一。它利用了簡單的數學變換（旋轉矩陣），在計算成本幾乎不變的情況下，實現了對相對位置的建模能力和長序列泛化能力。

在你構建或微調 Transformer 模型時，如果需要支持：

·更長的上下文窗口

·更強的相對位置感知

·更好的跨長度泛化能力

RoPE 是首選方案之一。

最後，我們回答一下文章開頭提出的問題。

1.為什麼不是加在 embedding 上，而是旋轉 q/k？

因為 RoPE 的核心目的不是告訴模型“這是第幾號 token”，而是告訴模型兩個 token 之間的相對距離。而注意力機制正是通過 qᵀk 來判斷關係的，所以將位置偏移編碼直接融入 q 和 k 更自然且高效。加法（如原始 PE）只給了“絕對位置”，而旋轉能建模“相對差值”。

2.RoPE 如何實現相對位置建模？

RoPE 的旋轉操作具有數學性質：

也就是説，旋轉後 qᵀk 的值只與位置差值 i − j 有關，這就自然實現了相對位置建模 —— 不關心你在哪兒，而關心你們之間相距多遠。

3.旋轉會破壞語義向量嗎？

不會。RoPE 的旋轉操作是一種保長（length-preserving）的線性變換（本質是二維向量在複數平面上的相位偏移），不會改變向量的模長，只會影響方向角度。在高維空間中，這種方式可以在不破壞語義結構的前提下，注入位置信息。