文章目錄
- 基本概念
- 實例
- Python實現
- 測試代碼
基本概念
要理解Tarjan算法，必須瞭解以下兩個概念，發現時間戳discovery time與低連接值low-link value。
發現時間戳這個很容易理解，Kosajaru算法沒有使用到發現時間戳，但是使用了結束時間戳。低連接值是一個強連通分量（以下簡稱SCC）裏所有節點的最小發現時間戳。也就是説一個SCC內，所有的點的低連接值相同。
圖拉真的算法其實很簡單，在DFS過程中，如果沒有環存在，那麼低連接值是等於發現時間戳的。什麼時候不會相等呢？產生回邊的時候，如果有回邊，那麼就更新當前低連接值為鄰居的低連接值，也就是父級節點的低連接值。在遞歸過程中，低連接值不斷傳遞。如果沒有遇到回邊，那麼節點就會被彈出，形成一個SCC。
實例
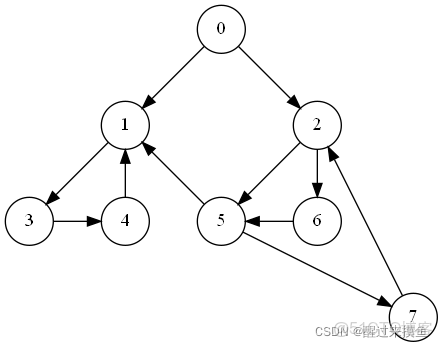
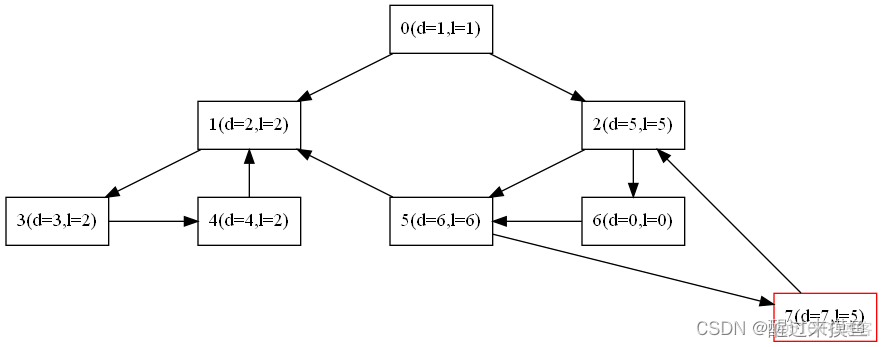
如以下圖：
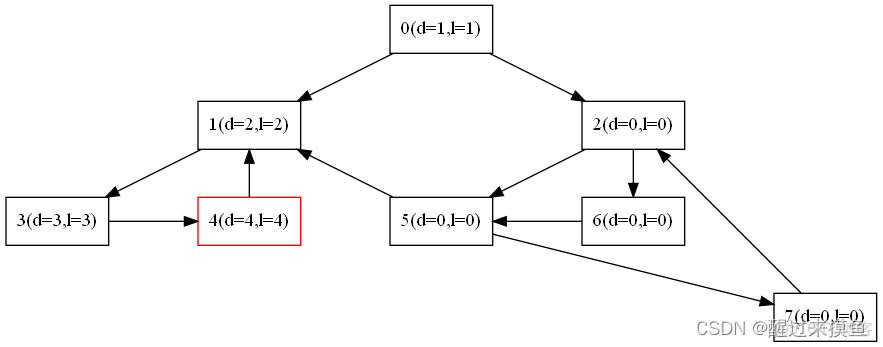
首先一直DFS下去，遇到一個回邊：
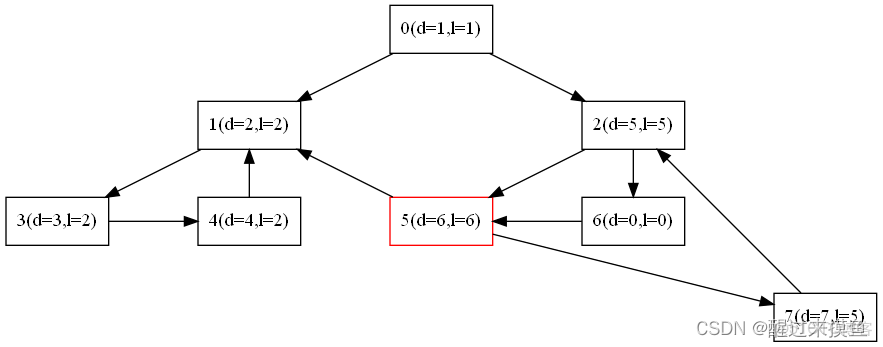
將其改成1的low值，也就是改成回邊的low值：
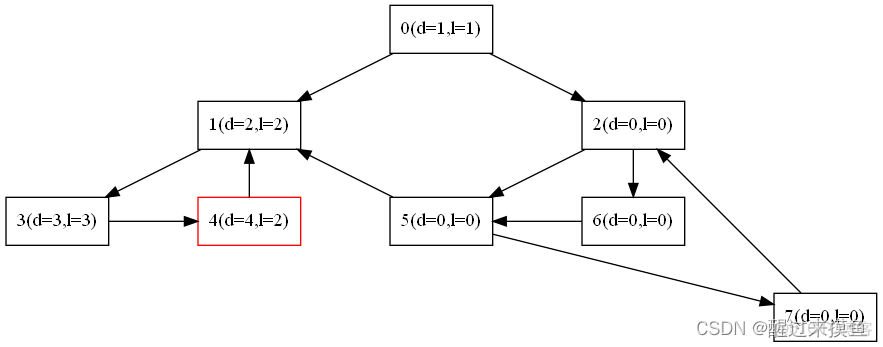
再是3：
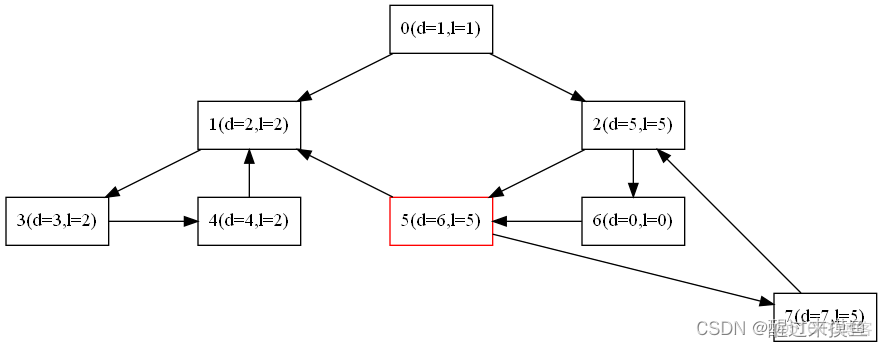
再是7：
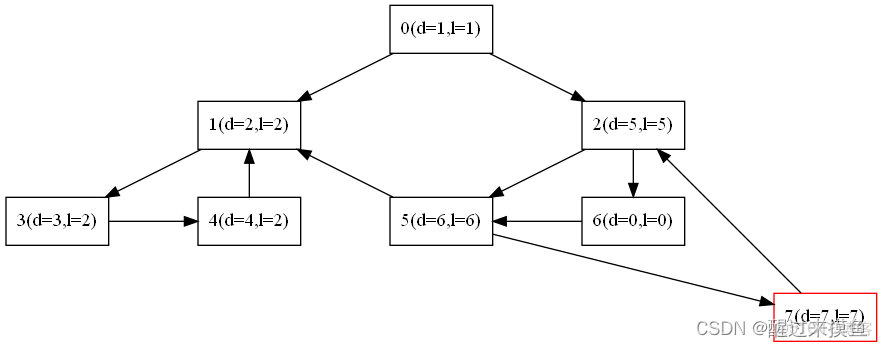
再是5,需要注意的是5不會更新1的low值，因為1已經被完全處理完了，已經彈出了棧：
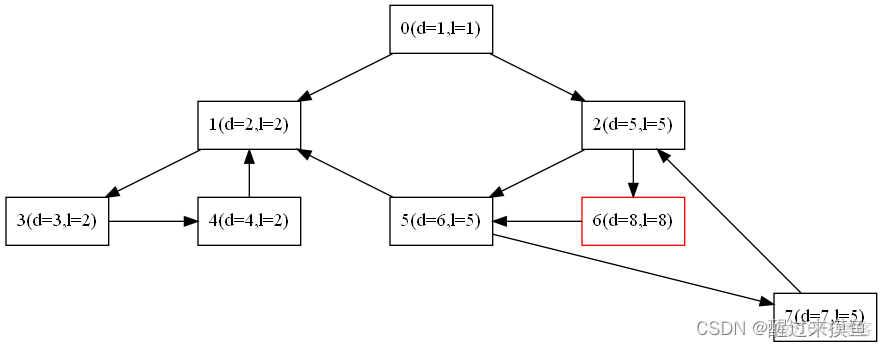
最後是6：
Python實現
# _*_ coding:utf-8 _*_
class UnweightedGraph:
def __init__(self, vertices, edges):
self.__vertices = vertices
self.__edges = edges
self.time = 0
n = len(self.__vertices)
self.disc = [0] * n
self.low = [0] * n
self.__pos = None
# 四種顏色
UNVISITED = 0
VISITED = 1
FINISHED = 2
POPPED = 3
def trajan(self):
n = len(self.__vertices)
self.time = 0
colors = [UnweightedGraph.UNVISITED] * n
stack = []
scc_list = []
for root in range(n):
self.dfs(root, colors, stack, scc_list)
return scc_list
def dfs(self, root, colors, stack, scc_list):
if colors[root] != UnweightedGraph.UNVISITED:
return self.low[root]
colors[root] = UnweightedGraph.VISITED
self.time += 1
self.disc[root] = self.time
self.low[root] = self.disc[root]
stack.append(root)
for neighbour in self.__edges[root]:
if colors[neighbour] == UnweightedGraph.POPPED:
continue
low_num = self.dfs(neighbour, colors, stack, scc_list)
if low_num < self.low[root]:
self.low[root] = low_num
colors[root] = UnweightedGraph.FINISHED
if self.low[root] == self.disc[root]:
scc_list.append(UnweightedGraph.get_scc(colors, stack, root))
return self.low[root]
@staticmethod
def get_scc(colors, trajan_stack, v):
scc = []
while len(trajan_stack) > 0:
x = trajan_stack.pop()
scc.append(x)
colors[x] = UnweightedGraph.POPPED
if x == v:
break
return scc
def to_dot(self):
s = 'digraph s {\nlayout=fdp\nnode[shape=box]\n'
for v in self.__vertices:
s += f'"{self.__vertices[v]}"[label="{self.__vertices[v]}(d={self.disc[v]},l=[{self.low[v]}])";pos="{self.__pos[v]}"];\n'
for i, e in enumerate(self.__edges):
for t in e:
s += f'\"{self.__vertices[i]}\"->"{self.__vertices[t]}";\n'
s += '}\n'
return s
@property
def vertices(self):
return self.__vertices
@vertices.setter
def vertices(self, value):
self.__vertices = value
@property
def edges(self):
return self.__edges
@edges.setter
def edges(self, value):
self.__edges = value
@property
def pos(self):
return self.__pos
@pos.setter
def pos(self, value):
self.__pos = value測試代碼
import unittest
from com.youngthing.graph.trajan import UnweightedGraph
class MyTestCase(unittest.TestCase):
def test_kosajaru(self):
# 以這個圖為例子：
vertex = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M']
edges = [
[5],
[0, 2, 6],
[3, 6],
[8],
[3, 9],
[1],
[7, 10, 11],
[3, 8, 11],
[2, 12],
[4, 8],
[11],
[12],
[11],
]
graph = UnweightedGraph(vertex, edges)
scc_list = graph.trajan()
for scc in scc_list:
print([graph.vertices[x] for x in scc])
print(graph.to_dot())
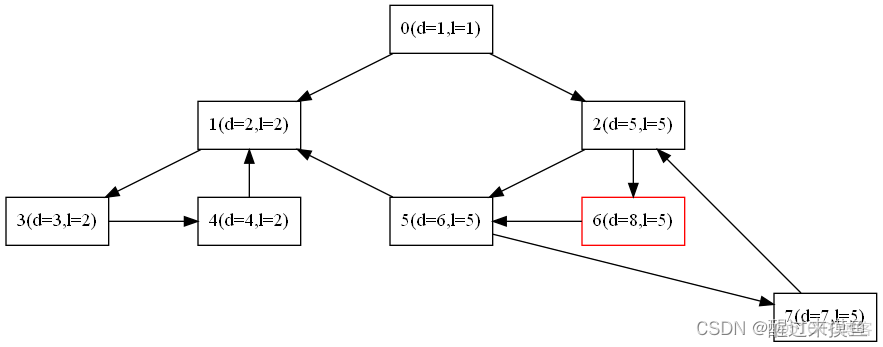
def test_nyu_data(self):
# 以這個圖為例子：
vertex = [0, 1, 2, 3, 4, 5, 6, 7]
edges = [
[1, 2],
[3],
[5, 6],
[4], # 3
[1], # $
[1, 7], # 5
[5], # 6
[2], # 7
]
graph = UnweightedGraph(vertex, edges)
graph.pos = ["0,0!", "-2,-1!", "2,-1!", "-4,-2!", "-2,-2!", "0,-2!", "2,-2!", "4,-3!"]
scc_list = graph.trajan()
for scc in scc_list:
print([graph.vertices[x] for x in scc])
print(graph.to_dot())
if __name__ == '__main__':
unittest.main()測試結果完全正確：
[4, 3, 1]
[6, 7, 5, 2]
[0]
本文章為轉載內容，我們尊重原作者對文章享有的著作權。如有內容錯誤或侵權問題，歡迎原作者聯繫我們進行內容更正或刪除文章。
