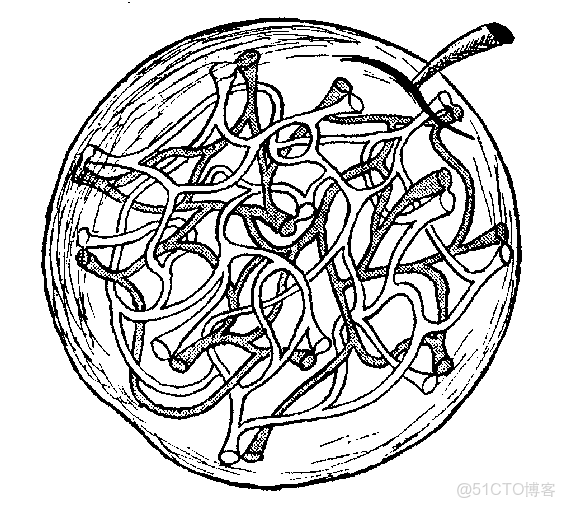
最近在看《一到無窮大》，其中第三章提到的雙蘋果模型一直不太理解。原文是這麼説的：

設想有兩個球體，各自限定在自己的球形表面內，如同兩個未削皮的蘋果一樣。現在，設想這兩個球體“互相穿過”，沿外表面粘在一起。或者，我們不如設想有個蘋果，被蟲子吃出彎曲盤結的隧道來。要設想有兩種蟲子，比如説一種黑的和一種白的；它們互相憎惡、互相迴避，因此，蘋果內兩種蟲蛀的隧道並不相通，儘管在蘋果皮上它們可以從緊挨着的兩點蛀食進去。這樣一個蘋果，被這兩條蟲子蛀來蛀去，就會像圖 18 那樣，出現互相緊緊纏結、佈滿整個蘋果內部的雙股隧道。但是，儘管黑蟲和白蟲的隧道可以很接近，要想從這兩座迷宮中的任一座跑到另一座去，卻必須先走到表面才行。如果設想隧道越來越細，數目越來越多，最後就會在蘋果內得到互相交錯的兩個獨立空間，它們僅僅在公共表面上相連。

一直想不清楚為什麼要兩個蘋果，一個蘋果不也是能形成這樣的形狀嗎？直到今天搞明白了。

首先這個雙蘋果模型並不是非常準確，原文説的黑白兩個蟲子的管道是不相交的，這個不相交的意義是在四維空間上的不相交，書中為了便於理解只能畫出三維空間中的不相交。其實四維空間的這兩個蟲子管道在三維的投影是完全有可能相交的，而且應該是重疊的。

為了便於理解，從一維空間説起：

一維空間就是一條線，如何讓這條線有確定的長度，但是沒有邊界呢？線段的邊界就是兩個端點，只要把另一條線段的兩個端點和這條線段的兩個端點相接，就形成了有固定長度，但是沒有邊界的一維空間。

二維空間就是一個面，這裏以一個圓形舉例，如何讓二維形狀有固定面積，但是沒有邊界呢？就是在圓形的邊緣與另一個圓形相接，這樣就有了面積固定，沒有邊界的二維平面。

三維空間就要用到這裏説的雙蘋果模型了，如何上三維形狀有固定體積，但是沒有邊界呢？思路和一維二維一樣，在它的邊界處連接上另一個三維物體，三維的邊界是就是每個蘋果的表皮，把表皮接在一起就是有固定體積，沒有邊界的三維形狀了。可以用上圖裏那個雙蘋果模型理解，但是切記，裏面的蟲洞，黑白兩個蟲子其實是在不同的三維蘋果裏，所以永遠不相交。