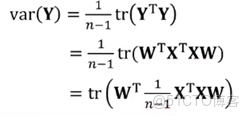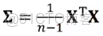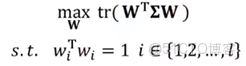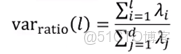特徵向量：設A是n階方陣，如果有常數λ和n維非零列向量α的關係式Aα=λα成立，則稱λ為方陣A的特徵值，非零向量α稱為方陣A的對應於特徵值λ的特徵向量。

特徵值分解：

在python中使用numpy工具就可以實現。

       降維

定義：將數據的特徵數量從高維轉換為低維。

作用：解決高維數據的維度災難問題的一種手段；能夠作為一種特徵抽取方法；便於對數據進行可視化分析。

 降維方法

主成分分析（PCA）

基本思想：構造原始特徵的一系列線性組合形成的線性無關低維特徵，以去除數據的相關性，並使降維後的數據最大程度地保持原始高維數據的方差信息。

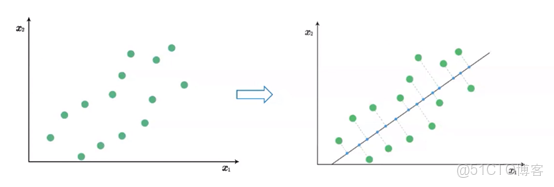
例：二維數據投影到一維（圖示）：

數據集表示：

數據集D={x1,x2,…,xn}，每個樣本表示成d維向量，且每個維度均為連續型特徵。數據集D也可以表示成一個n×d的矩陣X。為方便描述，進一步假設每一維特徵的均值均為0（中心化處理），且使用一個d×l的線性轉換矩陣W來表示將d維的數據降到l維（l<d）空間的過程，降維後的數據用Y表示，有Y=XW。

優化目標：降維後數據的方差：

 

 原始數據集的協方差矩陣

，則PCA的數學模型為：

模型求解：

 

做出以上處理之後，我們還需要將方差最大化：

 

取l個特徵值時首先進行降序排序處理。

算法流程：

 

l的選擇：

方差比例：通過確定降維前後方差保留比例選擇降維後的樣本維數l，可預先設置一個方差比例閾值（如90%），公式如下：

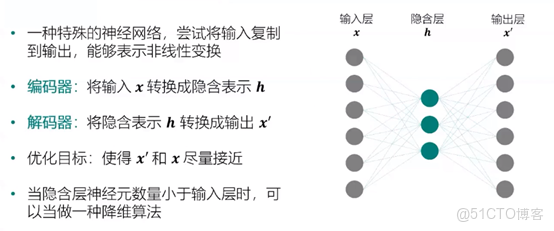
自編碼器：

 

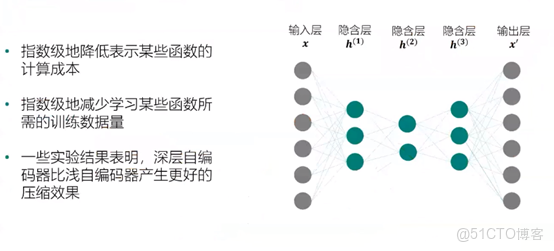
 深層自編碼器：