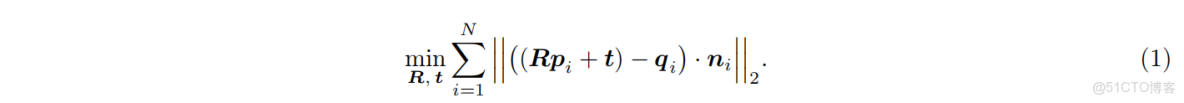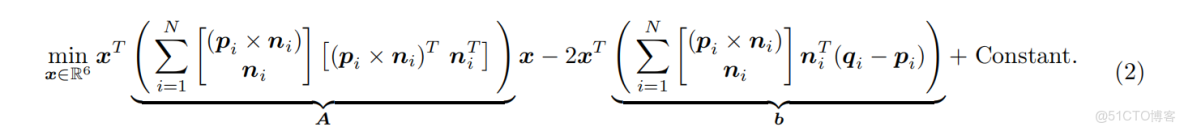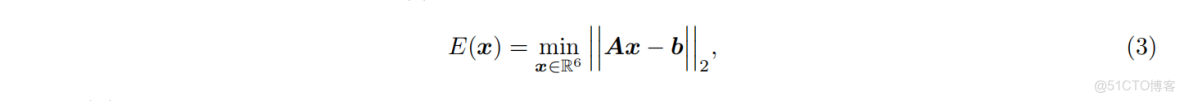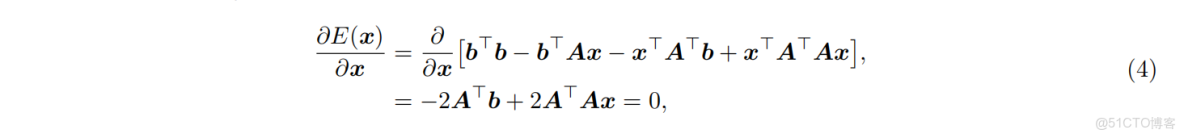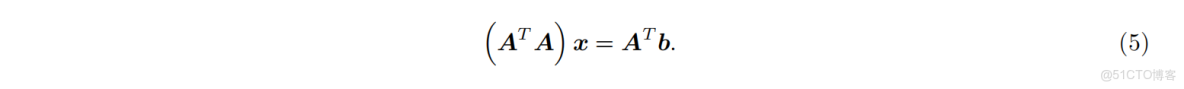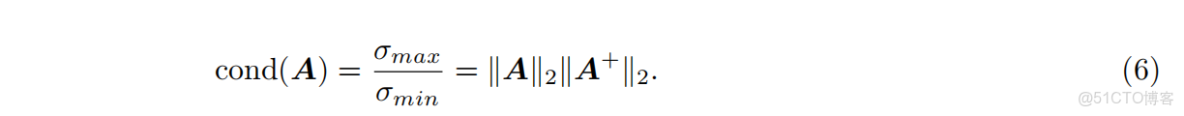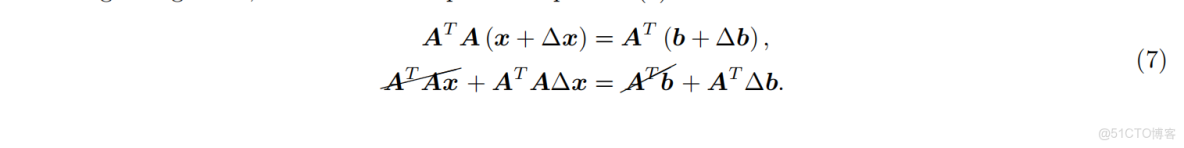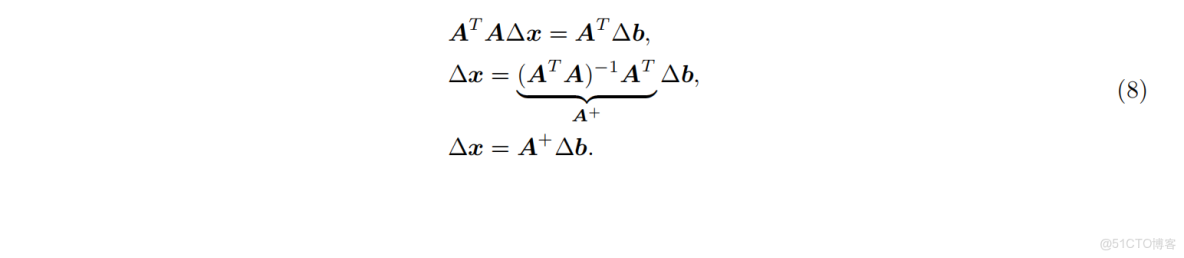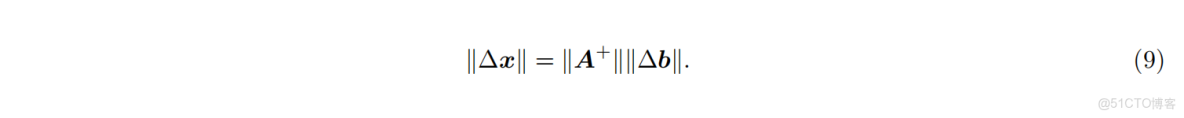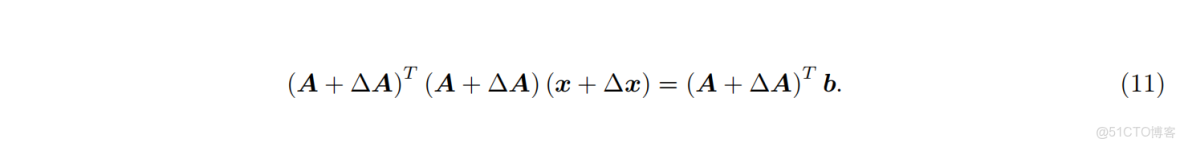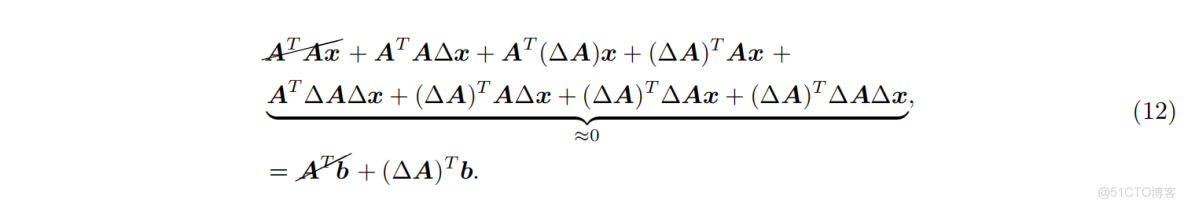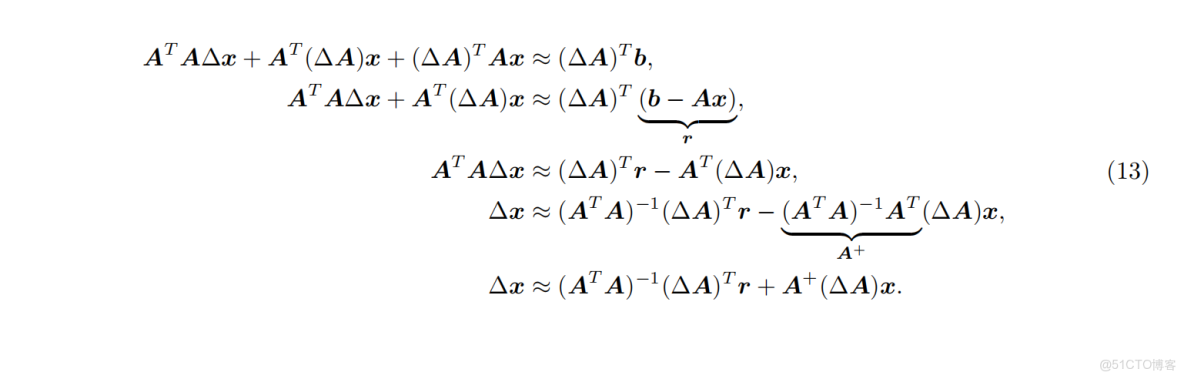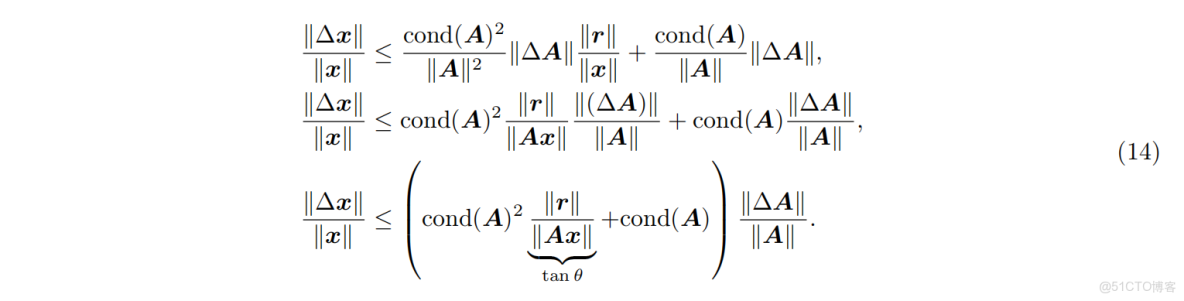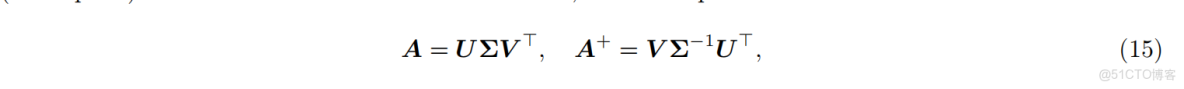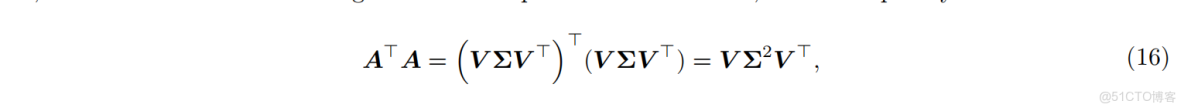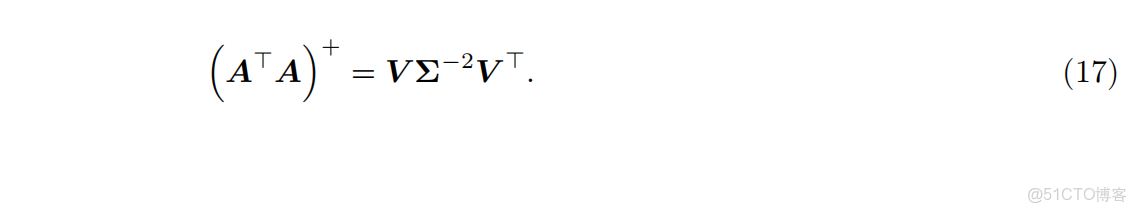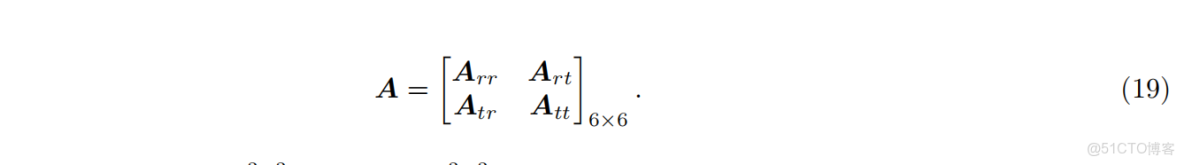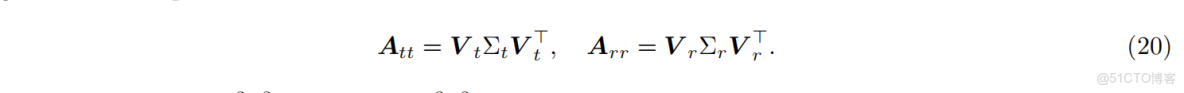一、文獻總結概述

1. 簡介

• 這篇論文研究的是 LiDAR 點雲配準（registration）中，當環境幾何結構不良（geometry‑poor／degenerate）的情況下，傳統配準方法（如 Iterative Closest Point, ICP）經常“失靈”：不收斂、或收斂到錯誤對齊／錯誤 pose。
• 作者系統地調查並比較了多種“退化 (degeneracy) 緩解 (mitigation)” 方法 —— 包括已有方法與新的嘗試 —— 目的在於提升基於 LiDAR 的定位 / SLAM 系統在“真實世界、複雜 / 極端 /幾何不良 (ill‑conditioned)”環境中的穩健性和可靠性。
• 論文在真實野外 (field) 與仿真 (simulated) 場景下進行了大規模實驗 (first time at this scale) 來驗證這些方法的效果。
  論文名“Informed, Constrained, Aligned (ICA)”也反映其方法論核心 (見下)。

---

2. 算法 / 研究 背景

背景：為何 “degeneracy” 是問題

• 點雲配準 (registration) — 尤其 ICP — 假設環境具有足夠豐富、多樣和非對稱幾何結構 (planes, edges, corners …) 使得優化 (least‑squares) 有良好約束。
• 但在很多現實場景 (例如隧道、空曠走廊、重複結構、對稱走廊、牆面、無人區、幾何單調 / 平坦 / 對稱環境) 中，這種假設破裂 —— 導致幾何信息不足 (degenerate / ill‑conditioned)，ICP 的 Hessian / 信息矩陣變病態 (ill‑conditioned)，優化變得不可靠、收斂性 / 精度很差。
• 現有實踐通常通過額外信息 (例如 IMU / odometry / GPS / loop‑closure / prior) 或後處理 (sensor fusion) 來“補償”幾何退化方向。但這種依賴外部信息的方法，不總是可行 (比如户外、未知環境、無 GPS、無 prior map、傳感器失敗等情況下)。

為什麼需要系統研究

• 雖然社區中已有一些“degeneracy‑aware”方法 (例如最近的 X-ICP) 提出約束 / localizability‑aware registration，但缺乏系統、廣泛 (多方法 + 多場景) 的對比和分析。
• 作者希望通過統一框架，對比許多策略 (active vs passive, hard vs soft constraints, regularization, global registration, etc.)，分析它們在真實場景下 (wild) 的表現 (not just synthetic toy cases)。

---

3. 文章貢獻（創新點）

主要貢獻可以總結為：

1. 首次大規模、系統性地對 degeneracy‑mitigation 方法進行對比分析，覆蓋多種方法、數據集、真實戰場 (field) 與仿真環境。
2. 引入多種 degeneracy‑aware 方法到 ICP / 點雲配準中，並對它們進行分類 / 定性＋定量評估：包括硬約束 (hard constraints)、軟約束 (soft constraints / regularization)、降維 / 子空間 (TSVD)、以及 global registration 等。
3. 敏感性分析 (sensitivity analysis) —— 對 least‑squares 優化在 ill‑conditioned 情況下的行為進行剖析，展示不同方法對 Hessian / 優化結構的影響，以及各方法在不同 degenerate 情況下的適用性 / 性能分佈。
4. 公開實現 (open‑source) + 實際 field experiments + 仿真，為社區提供可復現、可比較的 baseline；增強方法的可用性。

總體來説，這篇 paper 為點雲配準 / LiDAR‑SLAM 社區 系統化、嚴謹地處理 degeneracy 問題奠定了基礎。

---

4. 需解決的關鍵問題 / 挑戰

論文針對以下關鍵問題 (及挑戰)：

• 如何檢測 / 判斷退化 (degeneracy)? —— 也就是在優化 / 配準過程中，哪些“方向 / DoF (degrees of freedom)”是缺乏幾何約束 (under‑constrained) 的？
• 如何設計有效的緩解機制 (mitigation)？ —— 是依賴額外傳感器 / prior (passive)，還是修改優化 (active)？哪種機制更穩健 / 通用？
• 不同場景 (環境幾何條件) 下，各種方法的通用性 / 穩健性如何？ —— 不同退化類型 (平面、對稱、重複結構、噪聲、部分觀測、低重疊) 是否都能被同一方法覆蓋？
• 合理權衡精度 vs 穩健性 vs 計算開銷 —— 硬約束 / 正則 / 全局註冊 / 降維 /子空間 等方法，在現實 SLAM 中是否可實時 / 實用。
• 方法的可推廣性 / 可復現性 —— 不僅在 controlled 仿真實驗，而是在真實機器人 + LiDAR SLAM 流水線 (scan-to-map) 中是否可靠。

---

5. 論文提出的方法 (流程概覽 / ICA 框架)

論文總體採用的方法框架可以概括為 ICA (Informed, Constrained, Aligned) —— “知情 / 約束 / 對齊”。 具體流程 (high-level)：

1. 檢測 / 識別 degeneracy (degeneracy detection)

• 在每次 ICP / 點雲配準前 (或迭代中) 通過分析優化的 Hessian (或信息矩陣) / 特徵值 (eigenvalues) 來判斷是否存在 degenerate directions (ill‑conditioned directions) 。

2. 選擇合適的緩解 (mitigation) 方法 —— 方法體系包括：

• 硬約束 (hard‑constraint)：對檢測出的 degenerate directions 引入 equality / inequality constraints，禁止或限制在這些方向上的過大更新 (drift)。
• 軟約束 / 正則化 (soft‑constraint / regularization)：通過子空間截斷 (e.g. Truncated Singular Value Decomposition, TSVD)、Tikhonov 正則化 (線性/非線性) 等方式，抑制 ill‑conditioned 小特徵值對優化的影響。
• 全局註冊 (global registration)：在嚴重幾何退化 / 大變換 / 初值不佳 / 重疊較低時，使用 global registration 方法 (非迭代局部優化) 作為 fallback，以避免 local minima / drift。
• 混合 / heuristic 參數調優：對於 soft constraints，通過啓發式 (heuristic) 調整權重 / 參數，使其在複雜 / 退化環境中表現良好。

3. 實驗驗證 (simulation + real‑world field test)

• 在仿真環境 (controlled degenerate scenarios) 和真實機器人 + LiDAR SLAM pipeline (scan-to-map) 中測試各方法。
• 使用標準評價指標 (translational error, rotational error, convergence rate, robustness) 來比較方法性能。

---

二、文獻詳細內容

摘要（Abstract ）

ICP 配准算法在近十年來一直是基於 LiDAR 的機器人定位的首選方法。然而，即使在現代 SLAM 方案中，ICP 在幾何退化 (geometrically ill-conditioned) 環境下仍可能退化並變得不可靠。現有的解決方案主要集中於利用額外的信息來源，例如外部里程計 (odometry)，以替代優化解中的退化方向，或在傳感器融合設置中事後添加額外約束。

針對這一問題，本研究首次在文獻中大規模地調查並比較了新穎及已有的退化緩解 (degeneracy mitigation) 方法，以實現穩健的基於 LiDAR 的定位，並分析這些方法在退化環境中的有效性。具體來説，本研究探討了：

1. 對於 LiDAR 退化環境中 ill-conditioned ICP 問題，使用 主動 (active) 或 被動 (passive) 退化緩解方法的效果；
2. 首次評估 TSVD (Truncated Singular Value Decomposition)、不等式約束 (inequality constraints) 以及線性 / 非線性 Tikhonov 正則化在退化點雲配準中的應用。

此外，本研究對 ICP 問題的最小二乘 (least-squares) 優化步驟進行了敏感性分析，以更好地理解每種方法對優化的影響及其預期表現。

通過多次真實機器人實地 (field) 和仿真實驗驗證了分析結果。結果表明，對於缺乏可靠外部估計輔助的 LiDAR-SLAM，主動優化退化緩解方法 (active optimization degeneracy mitigation) 是必要且有利的；而在複雜、 ill-conditioned 場景中，經過啓發式參數微調的 軟約束方法 (soft-constrained methods) 可以提供更優的結果。

---

1 引言（Introduction）

光探測與測距 (LiDAR, Light Detection and Ranging) 傳感器能夠以高頻率提供精確的距離測量，使其非常適合在大規模環境中進行可靠的機器人位姿估計和精確建圖。同步定位與建圖 (SLAM, Simultaneous Localization and Mapping) 是在複雜和退化環境中操作機器人的關鍵工具 [Ebadi et al., 2024]。儘管 SLAM 和機器人定位也可以通過其他傳感方式實現 [Kazerouni et al., 2022; Khattak et al., 2020b; Nissov et al., 2024b]，但野外機器人研究領域主要關注改進基於 LiDAR 的 SLAM 技術，以在大規模環境中提高精度和魯棒性 [Bavle et al., 2023; Cadena et al., 2016; Ebadi et al., 2024; Nair et al., 2024]。

大多數被廣泛接受的 LiDAR-SLAM 框架利用點雲配準的高效性來生成準確的環境地圖。這些算法通過尋找六自由度 (6 Degrees-of-Freedom, DoF) 的剛體變換來對具有足夠重疊的點雲進行配準。一種成熟的點雲配準方法是迭代最近點 (ICP, Iterative Closest Point) 算法，廣泛應用於計算機視覺、三維位姿估計和機器人領域 [Li et al., 2023]。在典型的 LiDAR-SLAM 框架中 [Khattak et al., 2020a; Jelavic et al., 2022]，執行 LiDAR 掃描到地圖的配準，這對於將新信息與已生成的環境地圖對齊至關重要。

算法侷限性

儘管 ICP 成功且應用廣泛，但仍存在一些限制，包括：

1. 收斂到局部最小值的風險；
2. 對初始變換估計的不準確敏感；
3. 易受逐點特徵提取噪聲影響；
4. 在優化問題缺乏幾何約束時魯棒性不足 [Censi, 2007a; Brossard et al., 2020]。

值得注意的是，前三種誤差源可以通過修改 LiDAR-SLAM 框架直接解決，但優化問題本身的病態條件 (ill-conditioning) 直接源於環境中沿特定方向缺乏信息，因此難以克服。

LiDAR 退化的定義

根據文獻 [Tuna et al., 2023; Petracek et al., 2024; Gelfand et al., 2003; Hatleskog and Alexis, 2024]，LiDAR 退化指的是 ICP 算法優化過程的病態問題。如果 LiDAR 點雲信息不足，例如在自相似環境中幾何約束不足，優化狀態的一些線性組合可能變得不可觀測。在存在這些不可觀測優化狀態的情況下，ICP 優化被認為是病態、退化或不可定位的。

退化點雲配準

儘管機器人社區已經開發出在大多數環境中穩健運行的基於 LiDAR 的建圖框架 [Vizzo et al., 2023; Xu et al., 2022; Jelavic et al., 2022]，但在退化環境（缺乏足夠明顯特徵）下的點雲配準及隨後建圖仍然是一個挑戰，因為數據中缺乏必要的信息。針對這些場景的最新方法 [Tuna et al., 2023; Zhang et al., 2016; Westman and Kaess, 2019] 通常將問題分為兩個步驟：

1. 分析與檢測退化方向；
2. 緩解退化對優化的不利影響。

尤其是第一點受到了研究社區的廣泛關注 [Nobili et al., 2018; Ramezani et al., 2020; Tagliabue et al., 2020; Liu et al., 2021; Nubert et al., 2022b; Zhen et al., 2017; Zhen and Scherer, 2019; Tuna et al., 2023; Zhang et al., 2016]，而針對已檢測退化方向儘可能利用信息的工作則較少 [Nashed et al., 2021; Tuna et al., 2023; Zhang et al., 2016]。後者方法試圖緩解退化對優化的影響，並能夠充分利用位姿更新，至少在約束良好的優化方向上，而前者方法則完全跳過優化，依賴外部里程計傳播 ICP 位姿估計。如 [Tuna et al., 2023] 所討論的，完全跳過優化在 ICP 病態條件下僅在短時間內是可行策略，尤其是在初始配準估計不可靠且進一步微調點雲配準有益的情況下。

野外 LiDAR 退化緩解

隨着來自野外實驗的 LiDAR 退化機器人數據集逐漸可用 [Chen et al., 2024b; Nissov et al., 2024c; Tranzatto et al., 2022; Pfreundschuh et al., 2024]，機器人社區對在複雜退化環境中操作機器人越來越關注。儘管如此，一旦檢測到 LiDAR 退化，關於退化緩解方法有效性的研究仍存在基本空白。已有許多方法利用外部信息緩解 LiDAR 退化，例如基於因子圖優化的傳感器融合 [Jin and Jiang, 2024; Ebadi et al., 2021] 和濾波器 [Chen et al., 2024a]。然而，針對 ICP 基點雲配準的優化步驟進行處理 [Tuna et al., 2023] 或在 ICP 方法內緩解 LiDAR 退化仍然是一個未解決的問題。

本工作聚焦於在 ICP 公式中緩解 LiDAR 退化的方法，以縮小上述研究空白。ICP 中的退化緩解方法被分為兩類：被動 (Passive) 和主動 (Active) 退化緩解。

• 主動退化緩解 (Active degeneracy mitigation)： 如果方法輸出的任何顯式 LiDAR 檢測結果（例如 2.2.1 節）用於在 ICP 代價函數優化中採取行動緩解退化，則該方法被歸類為主動退化緩解。
• 被動退化緩解 (Passive degeneracy mitigation)： 與前者相反，如果 LiDAR 退化信息未在 ICP 配準中顯式使用以緩解退化，則稱其為被動退化緩解。

每類方法的相關工作將在 2.2.2 節中介紹。

本文貢獻

針對上述研究空白，本工作通過多種仿真和真實世界實驗（如圖 1 所示）研究並比較了新舊退化緩解方法，以分析複雜退化環境下點雲配準的有效性。除了研究結果外，本工作還提出了三種約束優化問題的方法，以實現穩健的點雲配準。最後，將研究結果與理論推導及最先進方法的侷限性結合，並通過多次機器人實地實驗和仿真示例進行驗證。本文主要貢獻如下：

1. 針對機器人在幾何退化的真實環境（如開闊自然場、城市隧道和複雜施工現場）中的操作，對不同約束類型在退化點雲配準任務中的有效性進行了系統研究；
2. 首次在文獻中引入、研究並討論了子空間 Tikhonov 正則化 (sub-space Tikhonov regularization)、截斷奇異值分解 (Truncated Singular Value Decomposition, TSVD) 和不等式約束 ICP 方法在退化點雲配準領域的應用；
3. 通過仿真示例和多次詳細的機器人實地實驗（使用步行機器人、行走式挖掘機以及手持不同 LiDAR 的實驗）對所討論方法進行公平、獨立的比較；
4. 整合開源方法與所有研究方法，並計劃統一開源，以促進未來開發面向退化感知 (degeneracy-aware) 的 LiDAR-SLAM 系統研究。

---

2 相關工作（Related work）

2.1 （魯棒）點雲配準

通過點雲配準實現快速且精準的位姿估計，是機器人感知領域數十年來的核心研究課題之一[Pomerleau et al., 2015]。在這一領域中，人們探索了多種方法族，例如：

• ICP 及其變體
  [Segal et al., 2009; Babin et al., 2021; Censi, 2008; Rusinkiewicz, 2019]
• 基於特徵的方法
  [Zhang and Singh, 2014; Behley and Stachniss, 2018]
• 概率模型方法
  [Biber and Straßer, 2003; Myronenko and Song, 2010; Maken et al., 2020]
• 深度學習方法
  [De Maio and Lacroix, 2022; Bai et al., 2021a; Nubert et al., 2021]
• 魯棒的全局配準方法
  [Zhou et al., 2016; Lim et al., 2022]

儘管已有大量進展，但由於其簡潔性與實用性，較為簡單的 ICP 變體仍然是最廣泛使用的基於 LiDAR 的點雲配准算法，例如：

• 點到點 ICP [Besl and McKay, 1992]
• 點到面 ICP [Low, 2004]
• 對稱點到面 ICP [Rusinkiewicz, 2019]
• G-ICP [Segal et al., 2009]

這些 ICP 方法的共同點是：通過反覆尋找兩幅點雲之間具有足夠重疊的對應點對，再迭代地最小化預定義的對齊度量，從而求解點雲間的六自由度剛體變換[Pomerleau, 2013; Li et al., 2023]。

---

另一方面，由於 ICP 方法容易陷入局部最優，研究者開始關注**全局最優且可驗證（certifiable）**的穩健點雲配準方法
[Yang et al., 2020b; Yang and Carlone, 2019; Carlone et al., 2015; Li et al., 2023; Lim et al., 2022, 2024]。這些算法能夠在異常值佔多數的情況下，依然保證估計結果為全局最優解。
同時，魯棒 M-估計器也被提出用於處理噪聲主導的點雲配準問題。這些估計器通過降低異常值權重來減輕其對代價函數的干擾。常見的 M-估計器包括：

• Welsch
• Tukey
• Cauchy
• Huber
• Geman-McClure

已廣泛用於機器人領域[Vizzo et al., 2023; Zhang et al., 2021; Babin et al., 2019]。最近，Babin 等人在 [2019] 中分析了不同魯棒範數在非退化配準問題中的有效性，並得出結論：如果參數調整得當，大多數魯棒範數在提高優化問題的信噪比方面表現相似。
為減少手動調參的需求，研究者提出：

• 自適應 M-估計器 [Chebrolu et al., 2021]，以應對不同輸入分佈
• 自適應非凸提升（Graduated Non-Convexity, GNC）
  [Yang et al., 2020a, 2020b; Briales and Gonzalez-Jimenez, 2017; Lim et al., 2022, 2024]
  以提高對大擾動的魯棒性。
  此外，受 ICP 在實際應用中成功的推動，研究者還從多個角度增強其魯棒性，例如：
• 改進特徵採樣
  [Kwok, 2018; Kwok and Tang, 2016; Petracek et al., 2024]
• 自適應匹配技術
  [Vizzo et al., 2023]
• 優化加速方案
  [Zhang et al., 2021]

---

然而，這些方法都沒有特別解決當點雲本身缺乏足夠信息（例如環境結構對稱或自相似）時的退化問題。這種情況在實際環境中十分常見，例如：

• 隧道
• 開闊平地
• 狹窄走廊
  [Tuna et al., 2023; Nubert et al., 2022b; Pfreundschuh et al., 2023]
  這些環境因缺乏足夠的幾何約束而導致 ICP 優化退化。

---

2.2 優化退化的檢測與緩解

2.2.1 優化退化檢測

配準不確定性

之前已有方法通過估計位姿估計過程的協方差來建模點雲配準的不確定性，並捕獲優化問題中的退化性 [Censi, 2007a; Brossard et al., 2020]。雖然這可能是一個良好的病態指標，但所得度量往往過於樂觀 [Bonnabel et al., 2016]。近期，[Talbot et al., 2023] 的作者進一步深入研究如何精確建模 LiDAR 點雲配準信息的不確定性，以作為鬆耦合測量用於多模態傳感器融合框架。更具體地，作者在 LiDAR SLAM 的背景下評估了 [Censi, 2007b] 中的 ICP 不確定性建模，併為降低計算量而簡化了跨協方差項。

類似地，在 LOG-LIO2 [Huang et al., 2024] 中，作者提供了一種增量式方法，以高效計算 LiDAR 測量的不確定性。他們提出的不確定性模型同時考慮了距離與方位角的不確定性，以及來自 LiDAR 激光束入射角與表面粗糙度的不確定性。隨後，該不確定性模型被整合進 LiDAR 慣性里程計框架中，以展示其在實際部署中的效益。作為最新的工作之一，[Hatleskog and Alexis, 2024] 提出了一種新的概率方法，通過考慮測量噪聲和表面法向估計噪聲，來估計優化方向退化的概率。

基於學習的方法

近期研究探索了數據驅動的方法來識別 LiDAR 信息的退化。[Gao et al., 2020] 通過融合協方差估計與環境信息量，引入了一種基於深度學習的熵指標。為避免機器人運行時複雜的蒙特卡洛採樣，[Nubert et al., 2022b] 建議使用合成數據進行訓練，並僅依賴當前 LiDAR 掃描來計算 6 自由度的可定位性指標。儘管數據驅動方法能夠通過建模高階動態來超越傳統方法，但其可解釋性仍然存在挑戰。

基於優化穩定性的方法

其他工作 [Cho et al., 2018; Tagliabue et al., 2020; Ebadi et al., 2021] 提議使用優化條件數作為整個 6 自由度位姿估計的綜合退化指標。類似地，CompSLAM [Khattak et al., 2020a] 使用 D-optimality 準則 [Arévalo, 2018] 來檢測多模態傳感器融合框架中的優化退化。基於類似的建模，[Hinduja et al., 2019] 採用優化的相對條件數作為退化檢測閾值，而不是最小特徵值。

作為早期開創性方法之一，[Zhang et al., 2016] 提出了一個稱為退化因子的檢測指標。該指標通過分析優化 Hessian 矩陣的最小特徵值來識別優化中的退化方向。類似地，DAMS-LIO [Han et al., 2023] 繼承了 [Zhang et al., 2016] 的思想，通過對優化 Hessian 的特徵值進行閾值處理來獲得退化方向，以用於基於濾波的狀態估計方法。

此外，[Bai et al., 2021b] 指出僅使用 Hessian 的最小特徵值在實際中並不可靠，因為需人為調節閾值。為解決這一問題，作者提出同時利用最小特徵值與條件數。近期，[Jin and Jiang, 2024] 使用最小特徵值和部分條件數提出了一個稱為“退化度（degenerate degree）”的指標。

考慮到為最小特徵值設定閾值的挑戰，[Lee et al., 2024] 提議使用卡方檢驗來計算歸一化特徵值的非啓發式（non-heuristic）閾值，隨後用這些歸一化特徵值檢測 LiDAR 與視覺優化問題中的退化方向。

在最新的工作中，[Ji et al., 2024] 提出一種點到分佈（point-to-distribution）的 ICP 退化檢測方法。利用其自適應體素化方法得到的概率分佈，作者證明該指標本質上與優化 Hessian 的特徵值相關。

細粒度方法

類似地，[Zhen and Scherer, 2019] 提出直接利用 Hessian 特徵空間估計環境的可定位性，通過度量點與法向約束對優化狀態的敏感度。基於該公式，[Zou et al., 2023] 從 LiDAR 測量生成信息矩陣來識別優化中的退化方向，並將其傳播至因子圖中用於精確的機器人位姿估計。

為了更細粒度的退化處理，X-ICP [Tuna et al., 2023] 提出一種基於對應關係的退化檢測方法，用於約束點雲配準的優化問題。該方法獨立考慮每個點到平面對應項的可觀性貢獻。沿着 X-ICP 的方向，[Chen et al., 2024a] 在配準步驟中提出利用點雲對應關係來檢測 LiDAR 退化。

---

2.2.2 機器人中的退化緩解

在複雜與非結構化環境中的機器人操作中，已有大量方法被提出以緩解 LiDAR 位姿估計方法中優化病態的問題。這些方法可根據其緩解退化的方式分為 被動(Passive) 或 主動(Active)。更明確地説，這取決於方法是否改變底層優化代價函數，或基於檢測到的退化信息來改變點雲配準產生的相對 LiDAR 位姿估計。技術細節在第 4 節介紹。

被動退化緩解

大多數被動方法使用補充傳感器模態進行傳感器融合 [Nissov et al., 2024c; Wen et al., 2024; Bai et al., 2021b]，或依賴外部里程計來源 [Khattak et al., 2020a; Pfreundschuh et al., 2023; Ebadi et al., 2021; Tagliabue et al., 2020]，以便在 LiDAR 退化時繼續傳播機器人位姿。

值得注意的是，[Lim et al., 2023] 使用了一種自適應參數設置策略來緩解 LiDAR 退化的影響。類似地，[Ferrari et al., 2024] 通過改進 ICP 的對應搜索來提高 ICP 質量，從而間接增強退化魯棒性。

基於對優化變量的分析，[Gelfand et al., 2003] 研究了點到平面 ICP 的幾何穩定性，並提出了一種基於採樣的方法來提取最具信息的掃描點，以改善優化問題的條件性。[Petracek et al., 2024] 提出減少輸入點雲中的信息冗餘。為此，作者採用了一種精細且退化感知的採樣策略，從而減輕 LiDAR 退化的負面影響。

主動退化緩解

[Floery, 2010] 是最早嘗試主動退化緩解的工作之一，通過為點雲配準添加額外約束來減少錯誤配準。類似地，[Olsson and Eriksson, 2008] 通過引入非線性等式約束來降低旋轉變量線性化帶來的誤差。

近期，[Zhang et al., 2016] 提出了 Solution Remapping 方法，將點雲配準所得的相對位姿更新投影到約束良好的方向上。X-ICP [Tuna et al., 2023] 中，作者提出沿退化方向加入硬約束來減少位姿估計誤差。

[Nashed et al., 2021] 在非線性最小二乘問題中使用額外的正則化項以緩解優化退化。此外，據作者所知，[Nashed et al., 2021] 是唯一對不同退化緩解方法進行比較的工作。使用 X-ICP 的約束優化，[Chen et al., 2024a] 提出在其約束型誤差狀態 IEKF 中使用檢測到的退化信息，以防止在退化方向使用 LiDAR 測量更新。然而，他們的比較有限，並未推廣至 SLAM 或點雲配準的實際應用。此外，[Nashed et al., 2021] 並未進行真實場地實驗，並且使用 RGBD 攝像頭而非 3D LiDAR。

儘管已有大量關於 LiDAR 退化的研究，但文獻仍缺乏關於如何有效利用 LiDAR 退化信息的全面分析。本工作在仿真與真實世界場景中深入分析並比較不同方法，以填補這一空白。

---

2.2.3 多傳感器融合與多模態退化緩解

除 LiDAR 中心的方法外，其他方法也關注利用補充的感知模態來緩解 LiDAR 退化帶來的不利影響。

COIN-LIO [Pfreundschuh et al., 2023] 利用 LiDAR 強度圖像的視覺特徵來補充 LiDAR 慣性框架中信息不足的方向。類似地，[Jin and Jiang, 2024] 使用超寬帶定位的約束補充 ICP 退化方向。此外，[Nissov et al., 2024c] 使用 LiDAR 與雷達模態構建因子圖滑動窗口平滑器，併為每個模態提供顯式退化信息。

近期，[Lee et al., 2024] 將 LiDAR、IMU 與視覺信息結合在一個位姿圖優化框架中，並在不同模態之間主動切換。作者分別檢測 LiDAR 與相機的優化退化，而不是依賴通用的協方差估計方法，如動態協方差縮放（DCS）[Agarwal et al., 2013] 或 fallback 圖 [Nubert et al., 2022a]。

在 DARPA SubT 挑戰 [Ebadi et al., 2024] 中，多項方法強調了退化感知 LiDAR-SLAM 的重要性。例如，CompSLAM [Khattak et al., 2020a] 使用退化檢測來切換傳感器模態，而 DARE-SLAM [Ebadi et al., 2021] 則通過在退化情況下阻止添加 LiDAR 因子來防止退化傳播。另一個方法 LION [Tagliabue et al., 2020] 通過測量多路複用器估計 LiDAR 因子的測量不確定性，以便在滑窗因子圖中穩健融合 IMU 數據。

為減少系統對單一模態的依賴，[Zhao et al., 2021] 提出運行三個並行位姿圖：一個用於 LiDAR-IMU，一個用於視覺-IMU，以及一個用於融合的中央 IMU 因子圖——這種依賴精確測量不確定性的方式展示了因子圖方法的高效性。在擴展該框架的基礎上，[Zhao et al., 2024] 提出預測 LiDAR 掃描的可觀性並將其作為協方差矩陣融入系統。

儘管這些方法提高了整個系統的魯棒性，但它們未從根本上解決 LiDAR 退化問題，而是依賴於外部傳感器融合來增強系統層級的魯棒性。本工作專注於研究如何在退化點雲配準框架內提升 LiDAR 位姿估計的質量與魯棒性。

---

3 問題分析與預備知識

本工作研究了不同優化退化緩解方法的優缺點。具體來説，本文考慮了在幾何上具有挑戰性的環境下，LiDAR-SLAM 中點雲配準的退化問題。本節將介紹點雲配準和退化檢測的預備知識。

3.1 點雲配準與 ICP

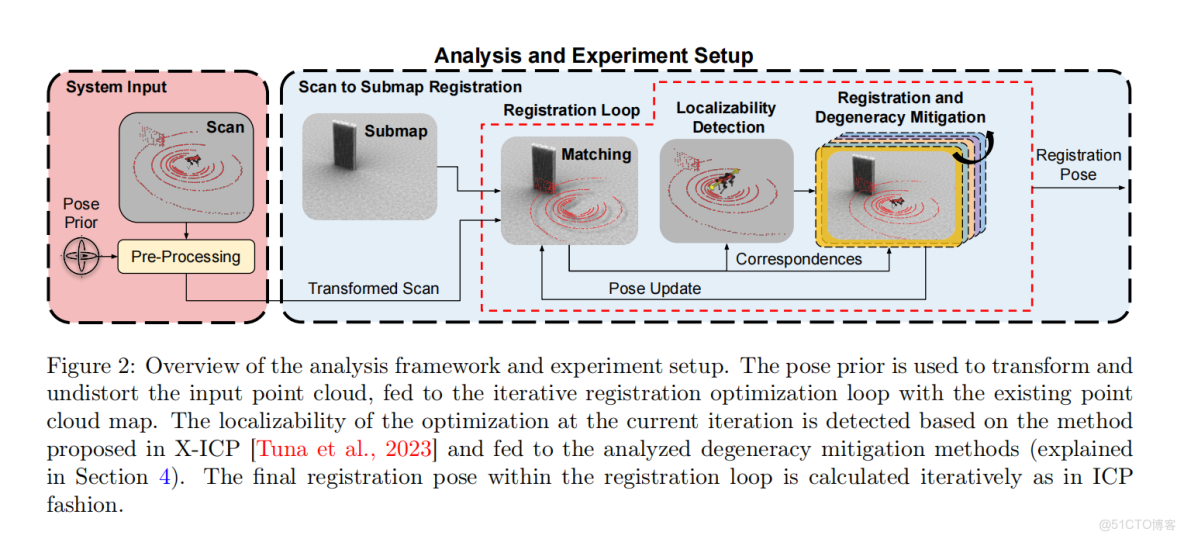
點雲配準問題旨在對齊兩個點雲，並獲得它們之間的相對剛性變換，如圖 2 所示。為了實現這一目標，已經提出了各種技術和度量方法，如第 2 節所討論。在本工作中，採用了帶點到平面（point-to-plane）代價函數的 ICP 算法 [Low, 2004]，因為它被機器人學界和許多點雲配準框架廣泛採用 [Jelavic et al., 2022; Tagliabue et al., 2020; Khattak et al., 2020a; Dellenbach et al., 2022; Pomerleau et al., 2013; Xu et al., 2022]。

具體來説，點雲配準側重於估計源點雲與參考點雲之間的齊次變換 ，源點雲和參考點雲的點數分別為 和 ，給定初始猜測 。

源點雲 表示在 LiDAR 座標系 中，而參考點雲 表示在（子）地圖座標系 中。齊次變換 包含旋轉矩陣 和平移向量 ，其中 。

對於源點雲中的每個點 ，在參考點雲中通過 K 最近鄰搜索找到最近的參考點 ，搜索過程中使用初始變換 ，如圖 2 中的匹配模塊所示。通常，將該變換作為初始猜測應用於 中的所有點，以獲得 ，從而改進匹配過程和優化收斂特性 [Brossard et al., 2020]，通過 ICP 的迭代過程實現。在本節其餘部分，所有變量均以（子）地圖座標系

對應關係搜索的結果可表示為一對多匹配 ，其中 ， 與 分別為源點雲和參考點雲匹配的點對，且 。

此外，, 表示參考點 的表面法向量，這是點到平面 ICP 代價函數所需的。匹配點的數量 表示優化問題的規模。點到平面 ICP 最小化問題的代價函數定義為：

公式 (1) 所示的問題可以按照 [Pomerleau et al., 2015] 中的推導，在引入標量三重積和旋轉矩陣線性化後，重寫為二次代價最小化問題：

其中， 為優化變量，其中平移部分 。旋轉向量 通過近似 表示，符號 （hat operator）將向量轉換為其對應的反對稱矩陣 。這裏， 是 SO(3) 羣的李代數，由 3×3 的反對稱矩陣組成。

將 和

其中 表示優化的殘差誤差，對該代價函數求最小值即可得到 Frobenius 範數（2-範數）解。此處， 表示優化問題的 Hessian 矩陣， 包含配準施加的約束。在每個線性化點上，都可以計算最優平移向量 和旋轉向量 。由於線性化誤差和對應點匹配誤差，ICP 的匹配和最小化操作需要迭代進行，直到收斂。

最小化問題公式 (1) 可以通過非線性求解器求解，如 高斯-牛頓法 (Gauss-Newton) 或 Levenberg-Marquardt (LM) 優化 [Agarwal et al., 2024]，也可以使用閉式解求解器，如 奇異值分解 (SVD) [Wall et al., 2003] 或 上下三角分解 (LU decomposition) 來求解公式 (3)。該操作對應於圖 2 中的退化緩解模塊。除第 4.1.6 節和第 4.2.1 節外，本工作採用 SVD 來求解公式 (3)，原因將在下文説明。

公式 (3) 的最小值出現在代價函數對

重新排列項後得到正規方程：

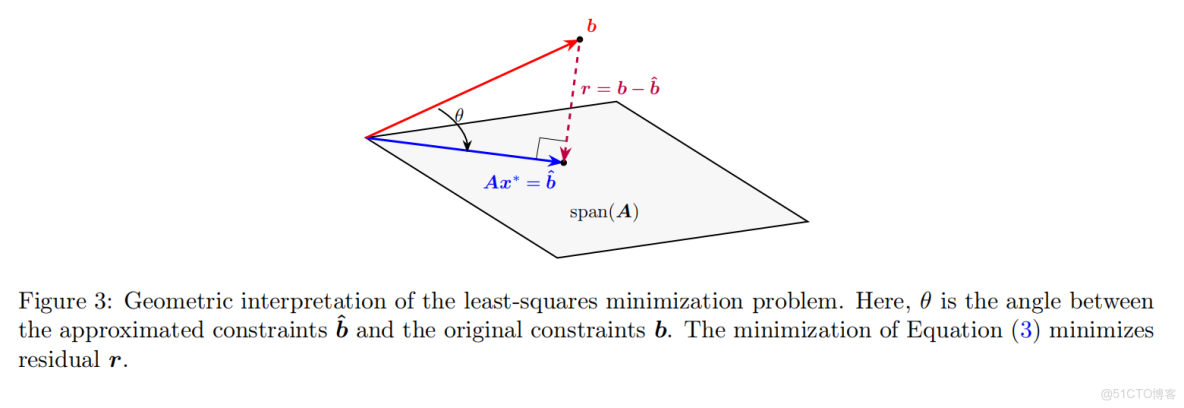
利用公式 (5) 可求解最小二乘問題，其幾何解釋為 在矩陣 ，如圖 3 所示。優化殘差可視為 到 。

---

3.2 最小二乘問題的敏感性

本節將前文介紹的方法與最小二乘最優化問題的敏感性和條件性聯繫起來。一個問題對輸入的小變化的敏感性被稱為該問題的條件性。如果輸入的小變化會導致輸出發生很大變化，則稱問題是病態（ill-conditioned），否則稱為良態（well-conditioned） [Heath, 2018]。

根據推導 [Golub and Van Loan, 2013; Heath, 2018]，矩陣

其中， 是 的偽逆。偽逆可以通過 的 SVD 計算，如第 3.3 節和公式 (15) 所述。此外， 和 分別表示

此前，作者 [Zhang et al., 2016] 對其退化檢測因子及方陣線性系統 的敏感性分析提供了詳細技術細節。然而實際上，ICP 的公式並不使用該等式，而是求解最小二乘問題，如第 3 節和公式 (5) 所述。最小二乘問題 的條件性不僅取決於矩陣 ，還取決於右端向量 ，因此僅用 並不足以刻畫敏感性。如圖 3 所示，當約束向量 接近 時，將產生較小的殘差，因此 的擾動對 的影響較小。可以推斷，當

來刻畫。

對

分析 對右端向量 改變的敏感性。為簡潔起見，以下使用 2-範數表示為 。設擾動為 ，由此產生 的變化為 ，則正規方程公式 (5) 可重寫為：

抵消原正規方程的項後得到：

取兩邊的 2-範數得到：

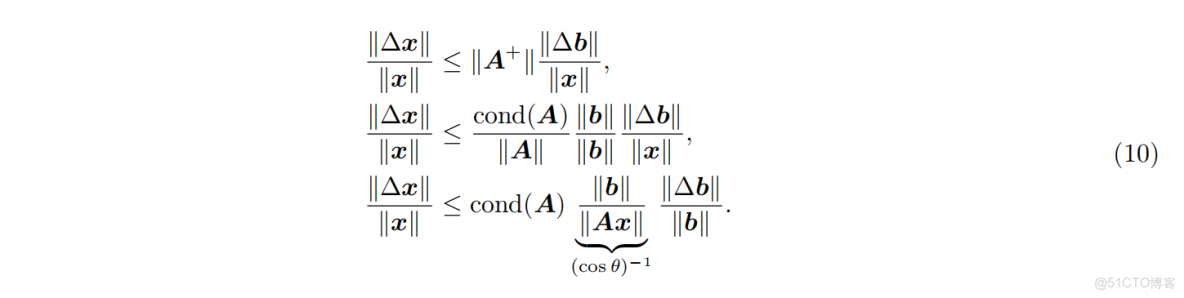
為了得到相對變化幅度，對兩邊除以 ，並結合 Cauchy–Schwarz 不等式 以及 ，得到：

公式 (10) 表明， 的敏感性不僅受 的影響，還取決於 是否能被 良好近似。當 時，有效條件數約為 ，而當 時，有效條件數會遠大於 。這説明，即使矩陣良態，如果

對

為了完整理解敏感性，也應考慮 的擾動。類似 的擾動，加入

展開並忽略高階項，抵消原正規方程的項，得到：

於是：

應用 2-範數並整理變量，得到相對變化的不等式：

公式 (14) 清楚地展示了最小二乘問題對 擾動的敏感性。可以看到，有兩項影響擾動在 上的傳播：一是矩陣 的條件數，二是與殘差 成比例並被 縮放的項。第二項尤其重要，因為任何殘留的 都會被 放大，對於病態問題至關重要。因此，最小二乘優化問題的有效條件性與矩陣

---

3.3 優化求解

在上一節中，分析了正規方程（公式 (5)）對 和

公式 (5) 可以通過高效的分解方法求解，例如 Cholesky 分解，前提是 不病態（即不接近奇異）。然而，由於本工作關注 LiDAR 的退化問題，因此優化問題可能是病態的，使用 Cholesky 分解並不具優勢。相反，採用 奇異值分解 (SVD)，該方法在對角化原矩陣的同時生成兩個正交基，用於求解該方程，尤其適用於病態優化問題，因為 SVD 解對所有（非方陣）矩陣均存在。

對於一個 的矩陣 ，SVD 分解定義為：

其中， 是 的旋轉矩陣， 是 的對角縮放與投影矩陣，包含矩陣 的奇異值， 是 的第二旋轉矩陣。此外， 是 的偽逆，在 滿秩的情況下，。對於對稱且正（半）定矩陣 ，SVD 與特徵值分解相同：

其中 是一個平方對角矩陣，其對角線元素為 的奇異值平方。矩陣 的右奇異向量 等價於 的特徵向量，而 的奇異值是

完成 SVD 分解後，得到的正交基與對角縮放矩陣可以用於偽逆計算：

將公式 (17) 與公式 (15) 代入公式 (5) 可得最優解：

由於 SVD 基於公式 (17) 中的偽逆操作，無論 的條件性如何，都可以求得最優 。然而，在優化病態方向上，該

類似地，SVD 對病態或接近秩虧的優化問題尤其有效，因為分解允許忽略接近零的奇異值。因此，最小二乘解對數據擾動的敏感性較低 [Heath, 2018]。這一特性被方法之一 Truncated SVD 所利用，詳見第 4.1.4 節。

---

3.4 LiDAR 退化檢測

當機器人在幾何特徵稀缺且環境複雜的場景中部署時，點雲配準可能變得病態（ill-conditioned）。因此，需要一種方法來檢測優化中的退化方向。由於本工作關注退化緩解，所有討論的方法均採用 X-ICP [Tuna et al., 2023] 中描述的退化檢測方法，以保證公平比較（對於所有需要位姿可定位性信息的方法）。該可定位性檢測過程在圖 2 中顯示為 localizability detection 模塊。

根據 [Tuna et al., 2023] 的推導，優化 Hessian 矩陣被劃分為子矩陣，以識別對應於優化變量 的旋轉部分 和平移部分

分解後的 Hessian 矩陣 和 分別對應旋轉信息和平移信息。此外，由於平移和旋轉在尺度和物理意義上存在差異，直接聯合處理 和 並不簡單，因此 和

其中， 和 是矩陣形式的特徵向量， 和 分別是 和 的縮放矩陣。 和 是 和

在本工作的其餘部分，通過結合 和 的特徵值，假設 和 的零空間近似是已知的。如果一個特徵向量 位於 或 的零空間中，則被標記為退化（不可定位），否則為非退化（可定位）。

此外，還考慮了映射關係 ，因為第 4 節中描述的一些方法期望退化特徵向量在 中，而其他方法期望在 中。此外，分別檢測平移和旋轉退化可以更精確地考慮 Hessian 矩陣 條目的尺度差異。基於這一考慮，交叉項 和

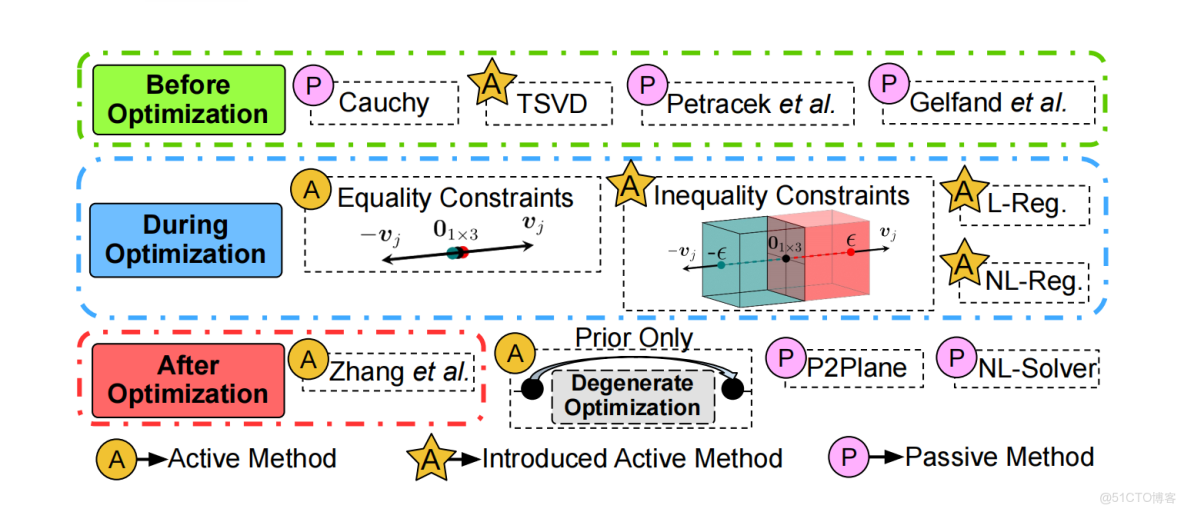
圖 4：
對所有研究方法的概覽圖，展示了這些方法在點雲配準流程的哪一個階段發揮作用。字母 P 和 A 分別表示被動（Passive）與主動（Active）退化緩解方法。符號 ⋆ 表示該方法在本研究中首次被用於退化點雲配準的場景。
其中，Zhang et al. 指代文獻 [Zhang et al., 2016]，Petracek et al. 指代文獻 [Petracek et al., 2024]，Gelfand et al. 指代文獻 [Gelfand et al., 2003]。