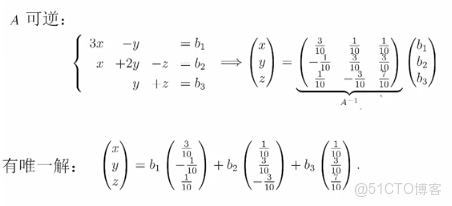總結：

1. 矩陣和線性方程組：A向量*x向量=b向量，Ab為擴展向量。有解：説明b向量可以被A向量線性表示；無解：説明b向量無法被A向量線性表示。

2.  線性方程的行圖和列圖

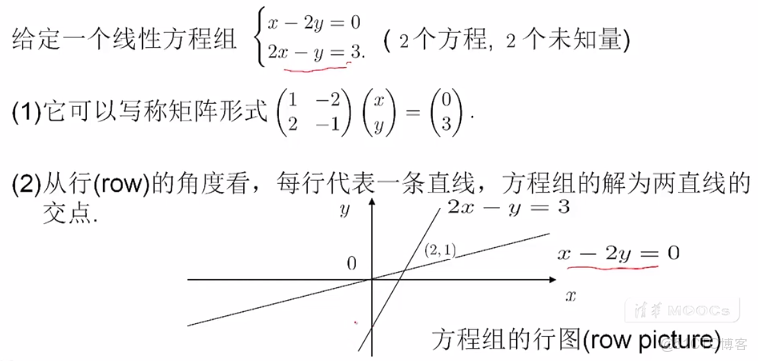
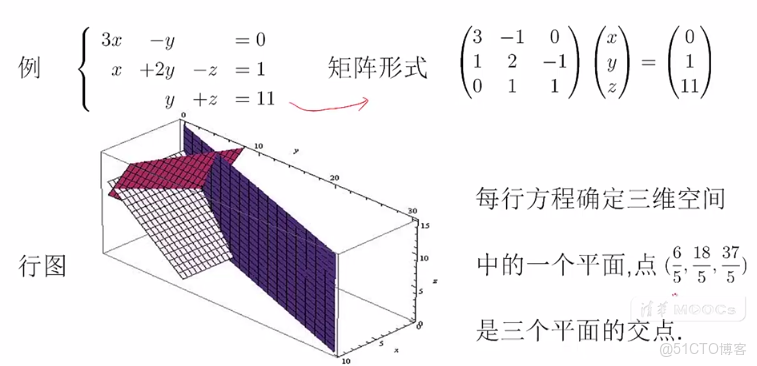
行圖：是從座標系的角度看線性方程，（2元/3元）方程組的每一行代表是一條直線/平面。有解：則在直線/平面間有交點。

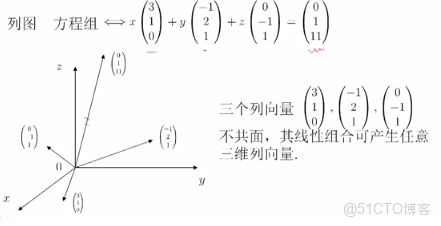
列圖：是從矢量的角度看線性方程。

 

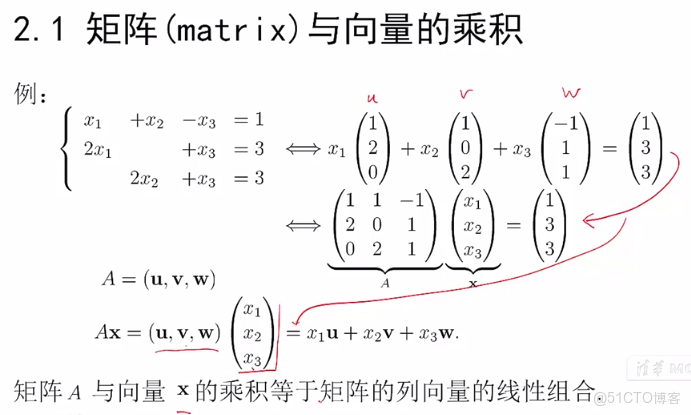
 2.1 矩陣與向量的乘積

我們可以將係數作為向量提出來，記為u，v，w，3個向量，並把3個向量組成3*3的A矩陣，並把x1，x2，x3做為一個向量，記成X。

上述方程也可以表述為矩陣的每一行與向量X的點乘的方程。

 

 

 2.2 可逆矩陣

定義：設A為n階方陣, 若存在n階方陣B, 使得AB = BA = In, 則稱A為可逆矩陣或非奇異矩陣, 而稱B 為A 的逆矩陣，並記為A-1.

逆矩陣的性質：

 

逆矩陣與線性方程: Ax = b, 如果b有唯一解，則A是可逆的。（有解説明A與b線性相關）

 

由於方程有解，b向量可以用A向量線性表示。可以寫成下面的的方程：X向量=S向量 * b向量，其中S向量為A向量的逆向量。

向量線性相關性（有解：線性相關；無解：線性無關）

 

多個向量間線性相關，則其中某個向量可以被其他向量線性表示。

 

 

 

2.3 線性方程組的行圖和列圖

行圖：是從座標系的角度看線性方程，（2元/3元）方程組的每一行代表是一條直線/平面。

列圖：是從矢量的角度看線性方程。

  

 

如果方程組有解，則在每行方程組，即這些直線和平面中有交點，無解，則沒有交點。有唯一解，則A可逆。

 

 

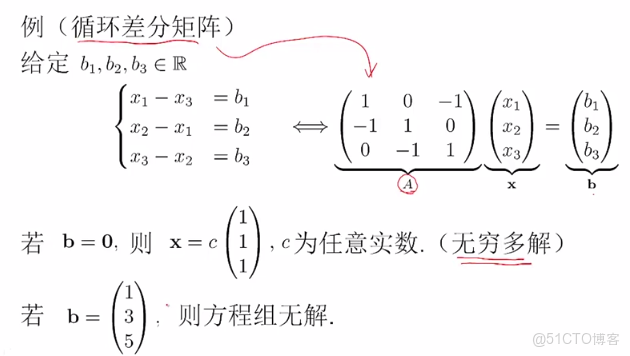
下面例子中，Ab擴展矩陣無解，所以b向量無法被A向量線性表示。A不可逆。