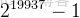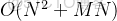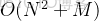以下文章專門面對 c++ & Windos 選手，使用其他語言或其他環境請另尋高明。
筆者是萬能頭文件黨，非特殊情況文章裏不會介紹頭文件使用（默認萬能頭）。
以下使用函數默認為 std 庫標準函數，即直接使用不加 std:: 的前綴。
有相當一部分題目的樣例十分寒磣，有時樣例全對但交上去不到 50 分。
這時候我們需要自己造數據，但一組組數據手動輸入等輸出肯定是不現實的。
解決這種問題需要用到對拍。
0.簡述
對拍，是一種進行檢驗或調試的方法，通過對比兩個程序的輸出來檢驗程序的正確性。
可以將自己程序的輸出與其他程序的輸出進行對比，從而判斷自己的程序是否正確。
一般我們對拍，需要四個程序：
（1）待測 / 出現錯誤的程序：sol.cpp (solution)
這是準備交上去的程序，已經儘量保證速度，但還未測驗正確性。
（2）暴力 / 標準的程序：bru.cpp (brute)
絕對正確。
（3）數據生成器：gen.cpp (generator)
這是你自己打的數據生成器，通常用隨機數函數生成。
保證這個程序輸出的都是符合題意，且完美覆蓋到所有邊界情況的數據。
（4）對拍腳本：st.cpp (stress test)
這是一個自動循環程序，將執行以下操作：
- 調用 gen.cpp 生成輸入
- 將輸入分別餵給 sol
.cpp和 bru.cpp- 比較兩個程序的輸出是否一致
- 若不一致，保存當前輸入並終止，便於調試
1.高質量隨機數生成
rand 家族
首先我們把目光放在隨機數生成函數上，相信大家都聽過 rand()
這個函數在 Linux 環境下的隨機數生成範圍是
，而在 Windos 環境下卻只有
，這太小了，完全不夠我們日常使用。
不但如此，rand() 即使有好種子作為生成基礎，但分佈和週期仍不佳，大量使用環境還是不推薦。
srand(time(0)); // 用當前時間作為種子
int x = rand() % 100; // 生成 [0, 99] 的隨機整數（如上為用每秒都變化（不易重複）的時間函數作為種子，種子可以理解為每次玩 mc 輸入的那個數字，憑藉這個種子生成地圖（隨機數）。一樣的種子生成的東西就一樣）
如果你做過隨機
亂搞
題，你應該對 random_shuffle()
它用於隨機打亂一個數組，同樣以 rand() 為基底，現已被時代淘汰。
如今我們要達到同樣的效果，會使用 shuffle 函數配上高質量隨機引擎（見下文代碼）。
高級貨 MT 19937
這個高質量隨機引擎名為梅森旋轉算法（Mersenne Twister），
是一種廣泛使用的偽隨機數生成器，週期為
，是一個梅森素數，因此得名。
具體使用如下：
#include
using namespace std;
#define uid uniform_int_distribution
// 這是一個 "一致分佈" 映射函數，後面經常跟着一段區間
// 用於把隨機數生成器生成出大的數映射到這段區間裏
// 大的數取模會有某個數字出現頻率更高的情況，而 uid 能保證所有數分佈概率一樣
// 當然，你如果要 long long 的直接改類型就好，就像這樣
// #define uid uniform_int_distribution
// 這樣後面跟着的區間就可以到 long long 的範圍
// 不過，區間常數也要是 long long 類型
// 比如這樣：dist(1, 1000000000000LL)
int main() {
// 我個人習慣關同步流，不關也行，關了快一點
ios::sync_with_stdio(false);
cin.tie(0);
// 創建一個 mt19937 類型的隨機數引擎 rng
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
// 這一大長串東西是一個時間戳，和 time(0) 差不多，但是納秒級精細度
// time(0) 是以每秒的時間做種子，在快速運行時可能連續幾次生成完全相同的數據
// 可能無法快速測到一些邊界情況
/* chrono::steady_clock::now() 獲取當前時間點（time_point）
.time_since_epoch() 從時間起點到當前時間的時長
.count() 將該時長轉換為一個整數（通常是納秒或微秒數）
*/
uid dist(1, 100); // 生成 [1, 100] 的隨機整數（嚴格閉區間）
cout << dist(rng) << "\n";
// 以後想生成 [1, 100] 的隨機整數，直接調用 dist(rng) 就好
// 還需要更多範圍的數
uid dist1(1, 10000); // [1, 10000]
uid dist2(1, 1000000); // [1, 1000000]
cout << dist1(rng) << "\n"; // 直接調用
cout << dist2(rng) << "\n";
vector v = {1, 2, 3, 4, 5};
shuffle(v.begin(), v.end(), rng); // 用 rng 打亂 vector
for (int x: v) {
cout << x << " ";
}
cout << "\n";
return 0;
}看起來多，真正用的時候，只需要記得這四句：
#define uid uniform_int_distribution
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
uid dist(1, 100);
cout << dist(rng) << "\n";多打幾遍，直到完全熟練。
例題實戰
接下來嘗試實戰下，以這道題為例：P1141 01迷宮 - 洛谷
大家可以自己先試試，然後用文件輸出看看生成的怎麼樣。
這裏提供標程：
// gen.cpp
// 生成 P1141 01迷宮 的合法測試數據
// Windows 下可用 g++ 或 MinGW 編譯運行
#include
using namespace std;
#define uid uniform_int_distribution
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
uid n_dist(1, 1000); // n 範圍 [1, 1000]
uid m_dist(1, 100000); // m 範圍 [1, 100000]
// ****真正使用時可以適當縮小數據範圍，防止暴力程序美美卡住 ***
int n = n_dist(rng);
int m = m_dist(rng);
cout << n << " " << m << "\n";
// 生成 n x n 的 01 矩陣
for (int i = 1; i <= n; i ++) {
for (int j = 1; j <= n; j ++) {
cout << (rng() & 1); // 快速生成 0 或 1
}
cout << "\n";
}
// 生成 m 個查詢
uid x_dist(1, n);
uid y_dist(1, n);
for (int i = 1; i <= m; i ++) {
cout << x_dist(rng) << " " << y_dist(rng) << "\n";
}
return 0;
}每道題都有不同的數據生成程序 gen.cpp，不過大部分都是換湯不換藥。
有一些特殊的，比如説生成無自環、無重邊的二叉樹，
就得在 gen 裏面加上一些小智慧或者算法（如 vector 記錄可作為父親的點，再隨機選取）。
這些我先暫時不講，後面有時間補上。
2.對拍腳本
這是很關鍵的一步，要保證你的程序能自個兒循環 or 找錯，對拍腳本是不能少的。
你需要先將四個程序（待測，暴力，數據生成，對拍腳本）全部放在同一個文件夾裏。
然後運行待測和暴力程序以及數據生成器，保存三個 exe 在上文的相同文件夾裏。
接下來運行這個程序：
// stress test
/*
x < y：將 x 作為 y 的輸入
x > y：將 x 的輸出寫入 y
其中 a 是程序，b 是文本
可以理解為尖尖朝哪邊，哪邊就是被放入數據的
*/
/*
system 函數是一個系統調用函數
成功了會返回 0，非成功返回非 0 （通常是 1）
*/
#include
using namespace std;
int main() {
// 這裏可不能關同步流！！不然沒緩衝看不到文字輸出
int tot = 0; // 計數的
// 循環持續生成測試數據並進行對拍，直到發現錯誤
while (1) {
tot ++;
cout << "Generating test case " << tot << "\n"; // 這裏用英文，有些環境下中文會亂碼
// 1. 調用數據生成器 gen.exe
// 將生成的測試數據放到文件 test.in（輸入數據） 裏
system("gen > test.in");
// 2. 運行第一個程序（sol.exe）
// 待測 sol 程序從 test.in 讀取輸入，將輸出放到 a.out
system("sol.exe < test.in > a.out");
// 3. 運行第二個程序（bru.exe）
// 暴力 bru 程序從 test.in 讀取輸入，將輸出放到 b.out
system("bru.exe < test.in > b.out");
// 4. 比較兩個輸出文件 a.out 和 b.out 是否一致
// fc 是 Windos 自帶文件比較函數
// 如果文件完全相同，fc 返回 0
// 如果文件不同，fc 返回非 0 值（通常為 1）
// system("fc a.out b.out") != 0，説明輸出不一致。
if (system("fc a.out b.out > nul")) {
// fc 會自動輸出一些東西，我們這裏用不到就把它放到 nul 空文件裏
cout << "The test case " << tot << " is wrong!" << "\n";
// 要把上面這句話放在 pause 上面才能看到
system("pause"); // pause 暫停程序，方便你查看控制枱輸出的差異信息
// 立即退出對拍器
// 此時 test.in 中保存的就是導致錯誤的輸入數據
// 可以用該數據單獨調試 sol 和 bru
return 0;
}
// 如果輸出一致，循環繼續，生成下一組測試數據
if (tot > 10000) { // 拍了一萬組
cout << "A possible solution." << "\n"; // 可能也許大概是正確的？
system("pause");
return 0;
}
}
}這個 Windows 腳本對於所有題都是適用的，只要你保證在同一個文件夾、有 exe、無同名程序。
3.待測程序與暴力程序
這個放到後面來講，是因為比起前面兩個，這倆玩意是因題而異。
就拿之前那道例題來説：P1141 01迷宮 - 洛谷
雖然聰明的同學們一看就知道是廣搜 + 帶權並查集，但假設我們還沒有那麼聰明。
傻傻的把每一個詢問點都拿去廣搜，也就有了我們的 70 分 TLE 暴力 bru 程序。
時間複雜度
：
// bru.cpp
#include
using namespace std;
const int N = 1010;
const int dx[4] = {0, 0, 1, -1};
const int dy[4] = {1, -1, 0, 0};
char s[N];
int a[N][N];
bool v[N][N];
int n, m;
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> (s + 1);
for (int j = 1; j <= n; j++) {
a[i][j] = s[j] - '0';
}
}
for (int i = 1; i <= m; i++) {
int x, y;
cin >> x >> y;
// 每次查詢清空 vis
memset(v, 0, sizeof(v));
queue Q;
Q.push((x - 1) * n + (y - 1)); // 0-indexed 每個點唯一編碼
v[x][y] = 1;
int cnt = 0;
while (!Q.empty()) {
int head = Q.front(); Q.pop();
int x = head / n + 1; // 轉回 1-indexed 行
int y = head % n + 1; // 轉回 1-indexed 列
cnt ++;
for (int d = 0; d < 4; d++) {
int xx = x + dx[d];
int yy = y + dy[d];
if (xx >= 1 && xx <= n && yy >= 1 && yy <= n && !v[xx][yy]) {
if (a[x][y] != a[xx][yy]) {
v[xx][yy] = 1;
Q.push((xx - 1) * n + (yy - 1));
}
}
}
}
cout << cnt << "\n";
}
return 0;
}然後我們再打一個待測程序，故意出錯，比如説點轉編號時錯誤。
以下程序通過樣例，但交上去 10 分，時間複雜度
。
// sol.cpp
#include
using namespace std;
const int N = 1010;
char s[N];
int a[N][N], mp[N][N];
int n, m;
int siz[N * N], fa[N * N];
int findfa(int x) {
if (fa[x] == x) return fa[x];
return fa[x] = findfa(fa[x]);
}
queue Q;
bool v[N * N];
int dx[4] = {-1, 1, 0, 0};
int dy[4] = {0, 0, -1, 1};
void bfs() {
while (!Q.empty()) {
int head = Q.front(); Q.pop();
if (v[head]) continue;
v[head] = true;
int x = head / n + 1, y = head % n;
// 如果 head 本來的點 y = n，那這裏轉編號就會錯
for (int i = 0; i < 4; ++i) {
int xx = x + dx[i];
int yy = y + dy[i];
if (xx < 1 || xx > n || yy < 1 || yy > n) continue;
if (a[xx][yy] == a[x][y]) continue;
int np = mp[xx][yy];
Q.push(np);
int tx = findfa(head);
int ty = findfa(np);
if (tx != ty) {
fa[tx] = ty;
siz[ty] += siz[tx];
}
}
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cin >> n >> m;
for (int i = 1; i <= n; ++i) {
cin >> (s + 1);
for (int j = 1; j <= n; ++j) {
a[i][j] = s[j] - '0';
mp[i][j] = (i - 1) * n + j; // 這裏 j 沒有 - 1
fa[mp[i][j]] = mp[i][j];
siz[mp[i][j]] = 1;
}
}
memset(v, 0, sizeof(v));
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
int id = mp[i][j];
if (!v[id]) {
Q.push(id);
bfs();
}
}
}
while (m--) {
int x, y;
cin >> x >> y;
int pfa = findfa(mp[x][y]);
cout << siz[pfa] << '\n';
}
return 0;
}4.實操
好啦，美美開工。
注意注意！！！這裏要先把 gen.cpp 的數據生成範圍改小，這樣才方便調試！
uid n_dist(1, 30); // n 範圍 [1, 30] uid m_dist(1, 500); // m 範圍 [1, 500]
不然暴力程序就會一直運行（畢竟時間複雜度高），出不來結果！
還有請事先保證：
sol.cpp和bru.cpp的輸出格式完全一致！（包括換行符、空格、無多餘空行），否則
fc可能誤報錯誤。
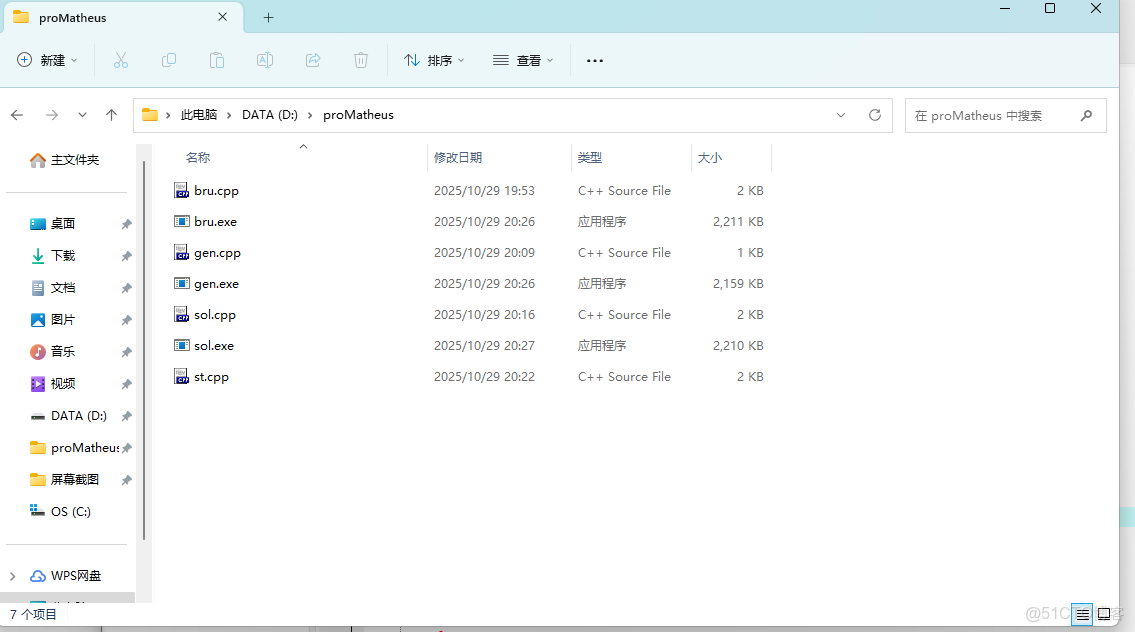
首先先建一個文件夾，為了模仿比賽，這裏建在 D 盤。
然後把所有程序都放進去，命好名，除了 st 都在 dev 裏運行得到 exe（點運行然後關掉黑框）。
搞好了就長這樣：
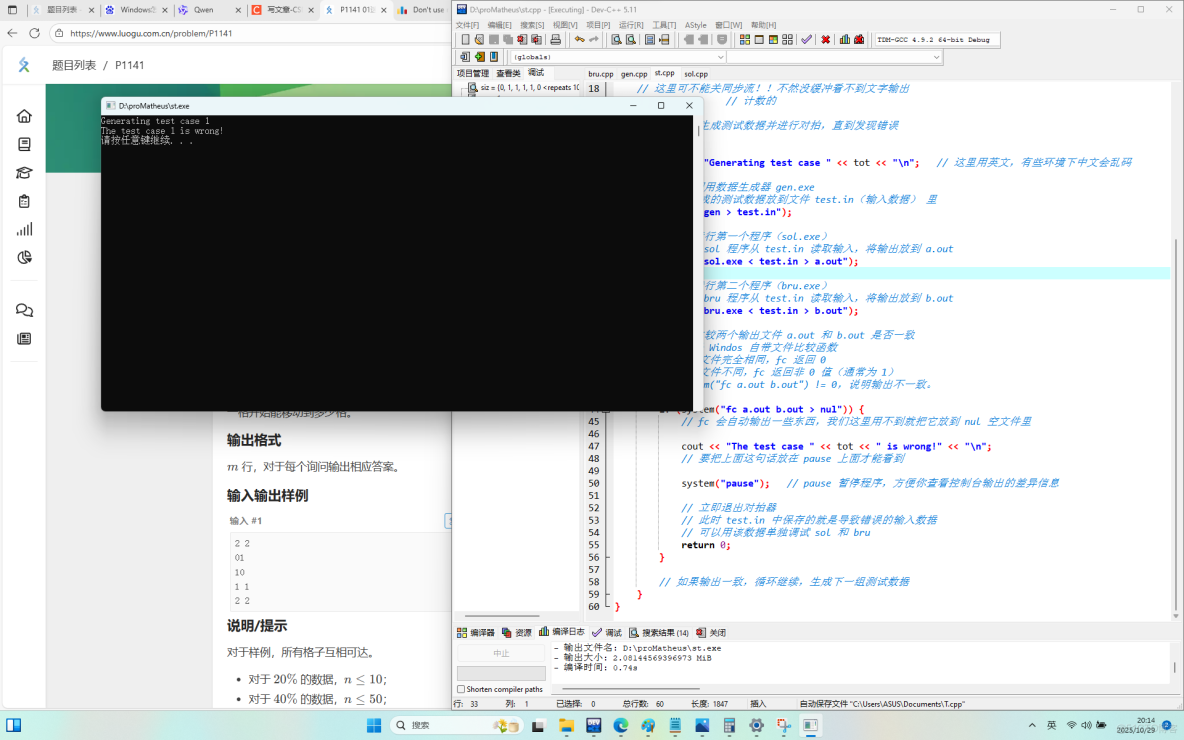
現在開始運行 st.cpp，會出現這樣：
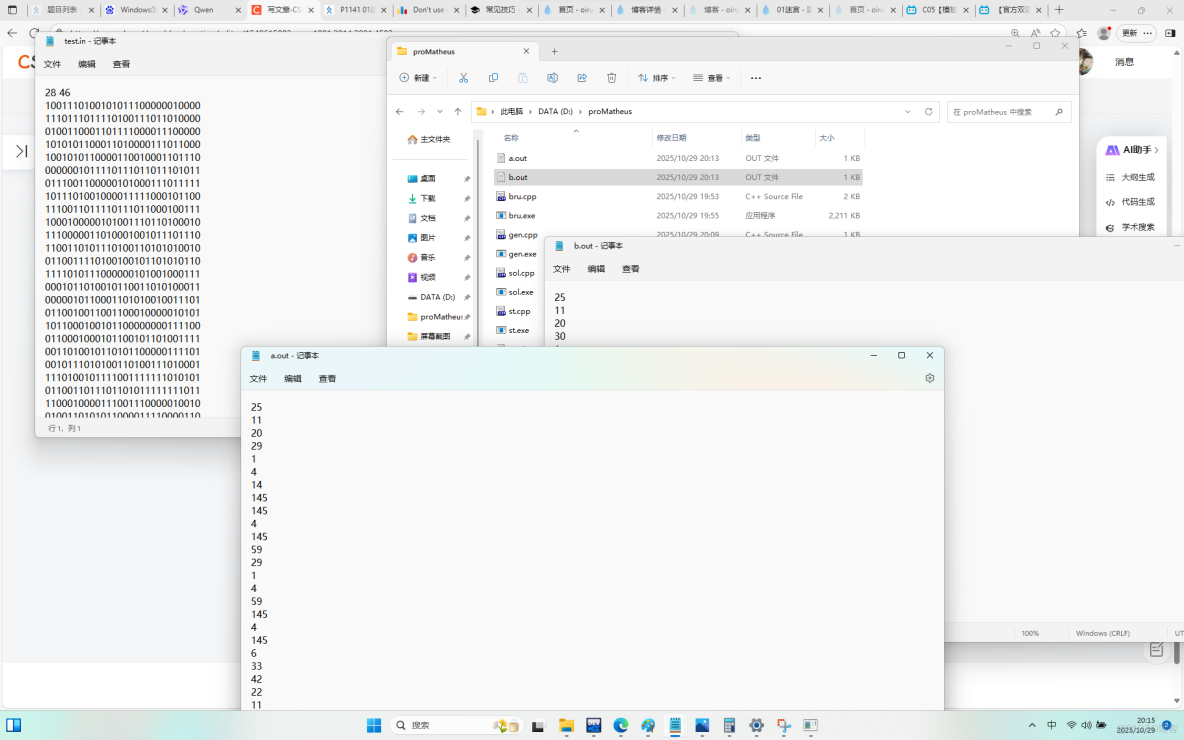
第一組就錯了，回到文件夾點開三個文本看看。
很好，找到問題！
修改完後，再次運行出 exe，運行下 st.cpp 看看。
（就是改了這兩句）
27 int x = head / n + 1, y = head % n + 1;
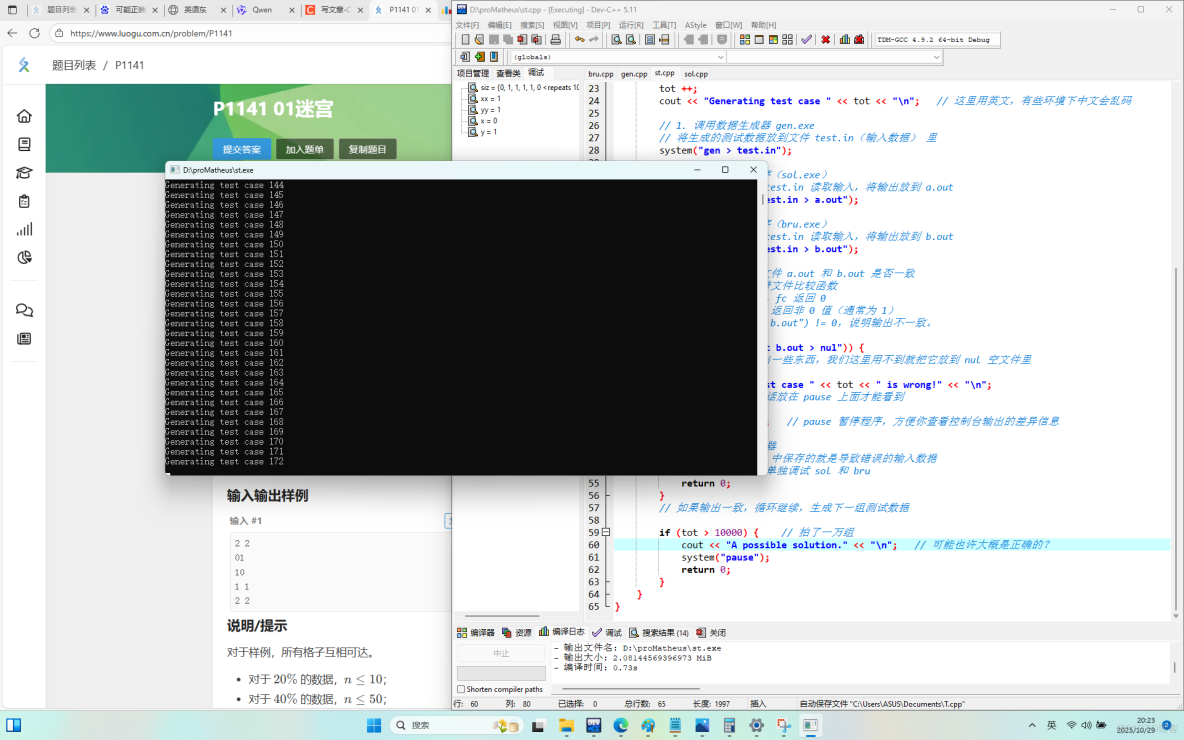
57 mp[i][j] = (i - 1) * n + j - 1;然後你就會看到：
嘛，如果你願意等
並且不怕電腦燒壞
的話，就可以拿到 "A possible solution." 成就！。
參考資料
常見技巧 - OI Wiki
Don't use rand(): a guide to random number generators in C++ - Codeforces
後記
對拍是很重要的技能，需要多練習。
但不要每道題都盲目使用對拍，進一步調試的前提是自己仔細檢查每一行代碼。
這算是幹了一件一直想幹的事情，希望能幫助到你。
後面會在這裏給一些鏈接，作為對拍例子博客。