目錄
一. 概念
二. 實現
1. 查找
2. 插入
3. 中序遍歷
4. 刪除
三. 遞歸版實現
1. 查找
2. 插入
3. 刪除
4. 析構、拷貝、賦值
非遞歸+遞歸整體代碼
四. 應用模型
1. key 的搜索模型
2. key_value 的搜索模型
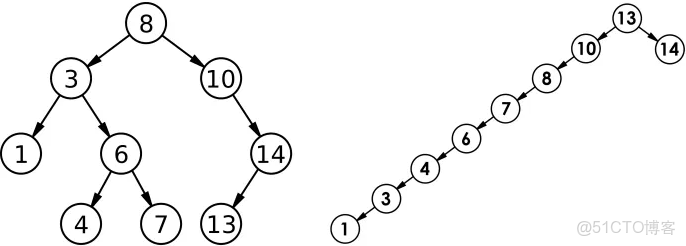
一. 概念
又稱二叉排序樹、二叉查找樹
性質、判定:
1. 若它的左子樹不為空,則左子樹上所有節點的值都小於根節點的值
2. 若它的右子樹不為空,則右子樹上所有節點的值都大於根節點的值
3. 它的左右子樹都是二叉搜索樹
二. 實現
BinarySearchTree.h
template<class K>
struct BSTreeNode
{
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
K _key;
BSTreeNode(const K& key)
:_left(nullptr)
, _right(nullptr)
, _key(key)
{ }
};
template<class K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
BSTree()
:_root(nullptr)
{ }
bool Insert(const K& key) {}
bool Find(const K& key) {}
bool Erase(const K& key) {}
void InOrder() {}
private:
void _InOrder(Node* root) {}
private:
Node* _root;
};
void TestBSTree1()
{
int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
BSTree<int> t;
for (auto e : a)
{
t.Insert(e);
}
t.InOrder();
t.Erase(4);
t.InOrder();
t.Erase(6);
t.InOrder();
t.Erase(7);
t.InOrder();
t.Erase(3);
t.InOrder();
for (auto e : a)
{
t.Erase(e);
}
t.InOrder();
}1. 查找
從根開始比較,查找,比根大則往右邊走查找,比根小則往左邊走查找
最多找高度次:O(N)
紅黑樹、AVL樹:O(logN)
bool Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
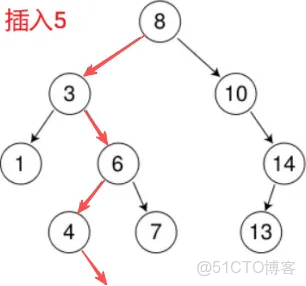
}2. 插入
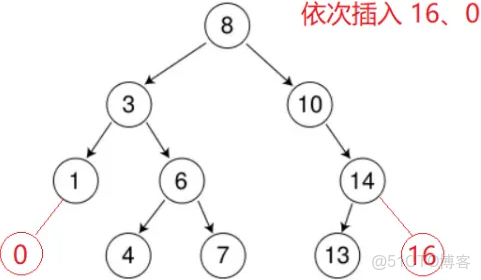
樹為空,則直接新增節點,賦值給 root 指針
樹不空,按二叉搜索樹性質查找插入位置,插入新節點
bool Insert(const K& key)
{
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key);
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}3. 中序遍歷
中序遍歷(左子樹、根、右子樹)二叉搜索樹的結果是排序的結果
void InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
InOrder(root->_left);
cout << root->_key << " ";
InOrder(root->_right);
}有問題,我們在外面用對象調用中序遍歷要傳私有成員變量 _root,但是私有我們不能在類外面用
BSTree<int> t;
t.InOrder();可以這樣解決:
void InOrder()
{
_InOrder(_root);
cout << endl;
}
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}4. 刪除
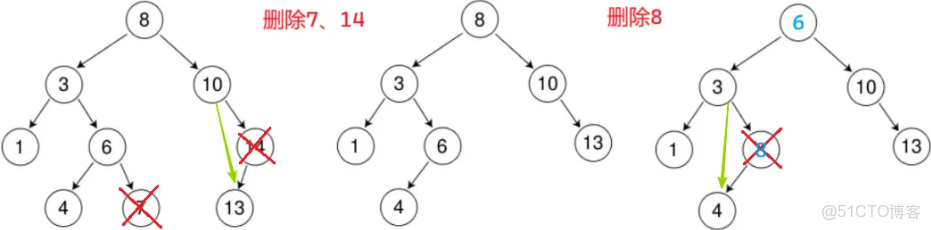
要刪的節點有3種情況:
1. 沒有孩子:託孤
2. 有1個孩子:託孤
3. 有2個孩子:和左子樹的最大節點(左子樹的最右節點) 或 右子樹的最小節點(右子樹的最左節點) 替換
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else // 樹中找到了要刪除的節點cur
{
// ......
delete cur;
return true;
}
}
return false;
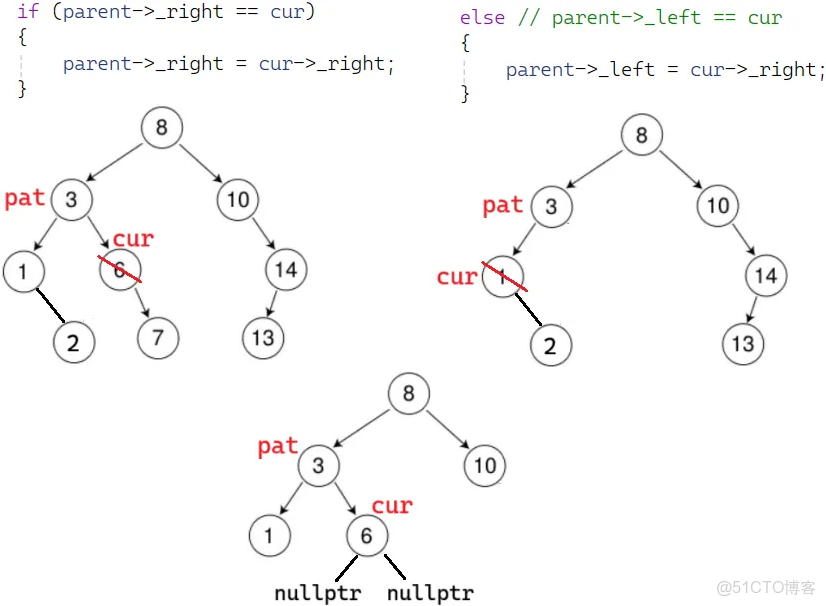
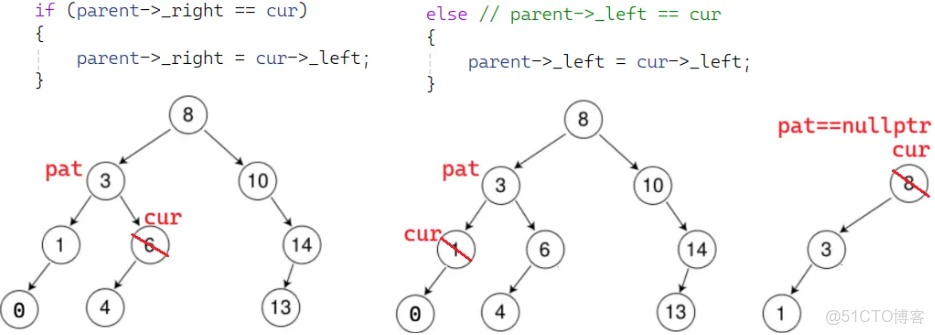
}cur 左為空(也解決了沒有孩子,左右都為空):
else // 樹中找到了要刪除的節點cur
{
// cur左為空
if (cur->_left == nullptr)
{
if (parent->_right == cur)
{
parent->_right = cur->_right;
}
else
{
parent->_left = cur->_right;
}
}
// ......
delete cur;
return true;
}但有這種特殊情況:
else // 樹中找到了要刪除的節點cur
{
// cur左為空
if (cur->_left == nullptr)
{
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (parent->_right == cur)
{
parent->_right = cur->_right;
}
else
{
parent->_left = cur->_right;
}
}
}
// ......
delete cur;
return true;
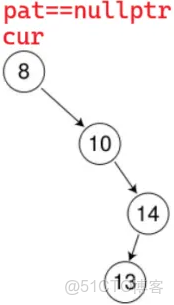
}cur 右為空:同理
else // 樹中找到了要刪除的節點cur
{
// cur左為空
if (cur->_left == nullptr) { }
// cur右為空
else if (cur->_right == nullptr)
{
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (parent->_right == cur)
{
parent->_right = cur->_left;
}
else // parent->_left == cur
{
parent->_left = cur->_left;
}
}
}
// ......
delete cur;
return true;
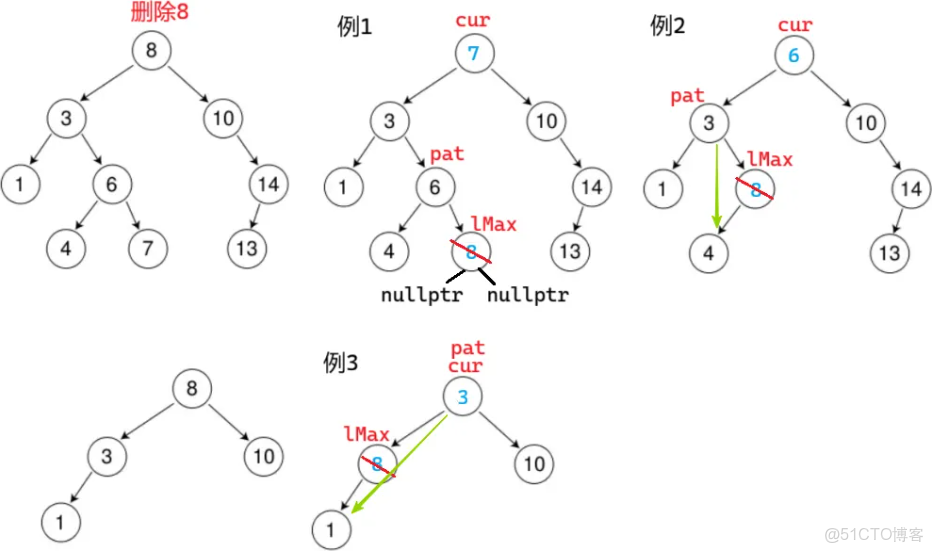
}cur 左右都不為空:替換以左子樹的最大節點(左子樹的最右節點)為例
注意:leftMax 是左子樹的最右節點,leftMax 這個節點一定不會有右子樹,可能有左子樹
注意:
這裏是左右都不為空的情況,而且我們要去左子樹找最右節點,所以 leftMax 可直接定義為 cur->_left;parent 可直接定義為 cur
如果 leftMax 定義為 cur,parent 定義為 nullptr,例3會坑
注意:替換後要通過找到父親直接刪(一定可以直接刪,因為 leftMax 右一定為空)。不能遞歸刪(7 < 8,在右子樹找,找不到,刪不了)。因為搜索樹的結構變了,而且無法傳根,無法控制;進而導致不滿足二叉搜索樹的性質
else // 樹中找到了要刪除的節點cur
{
// cur左為空
if (cur->_left == nullptr) { }
// cur右為空
else if (cur->_right == nullptr) { }
// cur左右都不為空
else
{
// 找替代節點
Node* parent = cur;
Node* leftMax = cur->_left;
while (leftMax->_right)
{
parent = leftMax;
leftMax = leftMax->_right;
}
swap(cur->_key, leftMax->_key);
if (parent->_left == leftMax)
{
parent->_left = leftMax->_left;
}
else // parent->_right == leftMax
{
parent->_right = leftMax->_left;
}
cur = leftMax;
}
delete cur;
return true;
}三. 遞歸版實現
C++裏,凡是樹形結構遞歸,都要單獨寫子函數。因為遞歸是子問題,要控制子樹
BinarySearchTree.h
template<class K>
struct BSTreeNode
{
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
K _key;
BSTreeNode(const K& key)
:_left(nullptr)
, _right(nullptr)
, _key(key)
{ }
};
template<class K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
BSTree()
:_root(nullptr)
{ }
void InOrder()
{
_InOrder(_root);
cout << endl;
}
bool FindR(const K& key)
{
return _FindR(_root, key);
}
bool InsertR(const K& key)
{
return _InsertR(_root, key);
}
bool EraseR(const K& key)
{
return _EraseR(_root, key);
}
private:
bool _FindR(Node* root, const K& key) {}
bool _InsertR(Node*& root, const K& key) {}
bool _EraseR(Node*& root, const K& key) {}
void _InOrder(Node* root) {}
private:
Node* _root;
};1. 查找
比根大,在右子樹找;比根小,在左子樹找;到空還沒找到,則不存在
bool FindR(const K& key)
{
return _FindR(_root, key);
}
bool _FindR(Node* root, const K& key)
{
if (root == nullptr)
return false;
if (root->_key < key)
{
return _FindR(root->_right, key);
}
else if (root->_key > key)
{
return _FindR(root->_left, key);
}
else
{
return true;
}
}2. 插入
插入的值 < 根:往左子樹去插入
插入的值 > 根:往右子樹去插入
插入的值 == 根:插入失敗
走到空的地方就可以插入
怎麼插入?new Node(key),但還要找父親,怎麼解決?加引用成為 Node*& root
這裏指針的作用:鏈接樹
這裏引用的作用:下一層改變影響上一層
bool InsertR(const K& key)
{
return _InsertR(_root, key);
}
bool _InsertR(Node*& root, const K& key)
{
if (root == nullptr)
{
root = new Node(key);
return true;
}
if (root->_key < key)
{
return _InsertR(root->_right, key);
}
else if (root->_key > key)
{
return _InsertR(root->_left, key);
}
else
{
return false;
}
}如果是空樹,root 是 _root 的別名,new 的第一個節點剛好給 _root
如果不是空樹,層層往下遞歸,前面的引用不起作用,每一層(每一個棧幀)都有一個引用
6 是對象,把左指針這個成員傳給下一層,下一層的 root 是 6 的左指針的別名(引用此時不發揮作用)
5 > 4,把 4 的右指針往下傳,root 是 4 的右指針的別名
4 的右指針為空 ==> 插入
new節點,給 root,對 root 修改,就是對 4 的右指針修改
這一句賦值,直接就鏈接上了,不用找父親,不用比較大小
3. 刪除
先找有沒有要刪的節點,找到了就刪,同樣分3種情況:左為空、右為空、左右都為空
bool EraseR(const K& key)
{
return _EraseR(_root, key);
}
bool _EraseR(Node*& root, const K& key)
{
if (root == nullptr) // 樹裏沒有
return false;
if (root->_key < key)
{
return _EraseR(root->_right, key);
}
else if (root->_key > key)
{
return _EraseR(root->_left, key);
}
else // 找到了,準備刪
{
Node* del = root;
if (root->_left == nullptr) // 1.左為空
{
root = root->_right;
}
else if (root->_right == nullptr) // 2.右為空
{
root = root->_left;
}
else // 3. 左右都不為空
{ }
delete del;
return true;
}
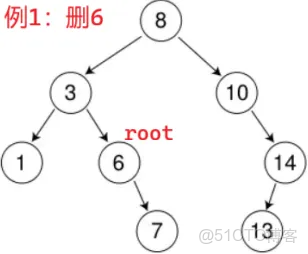
}3 < 6,3 的右指針往下傳,root 是 3 的右指針的別名
此時 root 是 6,找到了,開始刪:root 左為空,把 root(3的右指針)賦值為 root 的右指針
root 的右指針指向 7 ==> 3 的右指針指向 7,完成了鏈接關係
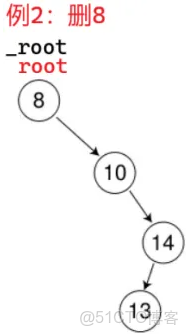
root 是 _root 的別名,上來就找到了,開始刪:
root 不為空,root = root->_right 就是 _root = _root->_right;
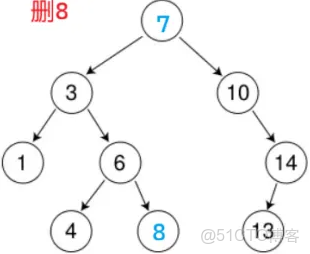
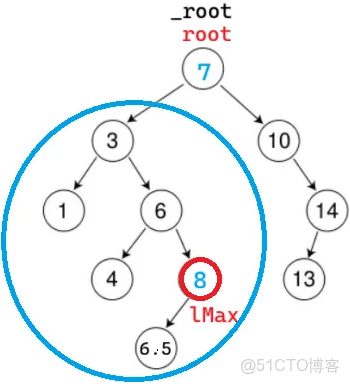
左右都為空:找替代節點(以找左樹的最右節點為例,最右節點的右一定為空)
以剛開始就找到要刪的 8 為例:
轉化為刪紅圈的節點。非遞歸實現一定可以找父親,直接刪;不能遞歸刪
我們現在有了引用,root 是 _root 的別名
但在 root 當前位置發揮不了作用,因為不需要改 _root,所以不能直接在最大的樹刪除
可以轉化為在藍圈的樹中刪,遞歸往下走,一定是右為空的情況。那時,root 是 6 的右指針的別名
走這個情形:
else // 3. 左右都不為空
{
Node* leftMax = root->_left;
while (leftMax->_right)
{
leftMax = leftMax->_right;
}
swap(root->_key, leftMax->_key);
return _EraseR(root->_left, key);
}這種方法在替換後,會在左子樹再找一遍要刪除的節點,但代價不大
第11行遞歸進去之後,不會再次走這個左右都不為空的 else
4. 析構、拷貝、賦值
析構:析構也得寫子函數,因為要遞歸,析構函數都沒有參數
二叉樹:用後序遍歷刪除,循環不好用
拷貝:不能調 Insert,會改變樹的形狀
走前序遍例賦值
默認的拷貝構造是淺拷貝,會出錯,要自己實現深拷貝
賦值:現代寫法
BSTree(const BSTree<K>& t)
{
_root = Copy(t._root);
}
BSTree<K>& operator=(BSTree<K> t)
{
swap(_root, t._root);
return *this;
}
~BSTree()
{
Destroy(_root);
}
void Destroy(Node*& root)
{
if (root == nullptr)
return;
Destroy(root->_left);
Destroy(root->_right);
delete root;
root = nullptr; // 這就是傳引用的原因
}
Node* Copy(Node* root)
{
if (root == nullptr)
return nullptr;
Node* copyroot = new Node(root->_key);
copyroot->_left = Copy(root->_left);
copyroot->_right = Copy(root->_right);
return copyroot;
}非遞歸+遞歸整體代碼
template<class K>
struct BSTreeNode
{
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
K _key;
BSTreeNode(const K& key)
:_left(nullptr)
, _right(nullptr)
, _key(key)
{ }
};
template<class K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
BSTree()
:_root(nullptr)
{ }
BSTree(const BSTree<K>& t)
{
_root = Copy(t._root);
}
BSTree<K>& operator=( BSTree<K> t)
{
swap(_root, t._root);
return *this;
}
~BSTree()
{
Destroy(_root);
}
bool Insert(const K& key)
{
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key);
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
bool Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else // 樹中找到了要刪除的節點cur
{
// cur左為空
if (cur->_left == nullptr)
{
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (parent->_right == cur)
{
parent->_right = cur->_right;
}
else // parent->_left == cur
{
parent->_left = cur->_right;
}
}
}
// cur右為空
else if (cur->_right == nullptr)
{
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (parent->_right == cur)
{
parent->_right = cur->_left;
}
else // parent->_left == cur
{
parent->_left = cur->_left;
}
}
}
// cur左右都不為空
else
{
// 找替代節點
Node* parent = cur;
Node* leftMax = cur->_left;
while (leftMax->_right)
{
parent = leftMax;
leftMax = leftMax->_right;
}
swap(cur->_key, leftMax->_key);
if (parent->_left == leftMax)
{
parent->_left = leftMax->_left;
}
else // parent->_right == leftMax
{
parent->_right = leftMax->_left;
}
cur = leftMax;
}
delete cur;
return true;
}
}
return false;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
bool FindR(const K& key)
{
return _FindR(_root, key);
}
bool InsertR(const K& key)
{
return _InsertR(_root, key);
}
bool EraseR(const K& key)
{
return _EraseR(_root, key);
}
private:
void Destroy(Node*& root)
{
if (root == nullptr)
return;
Destroy(root->_left);
Destroy(root->_right);
delete root;
root = nullptr; // 這就是傳引用的原因
}
Node* Copy(Node* root)
{
if (root == nullptr)
return nullptr;
Node* copyroot = new Node(root->_key);
copyroot->_left = Copy(root->_left);
copyroot->_right = Copy(root->_right);
return copyroot;
}
bool _FindR(Node* root, const K& key)
{
if (root == nullptr)
return false;
if (root->_key < key)
{
return _FindR(root->_right, key);
}
else if (root->_key > key)
{
return _FindR(root->_left, key);
}
else
{
return true;
}
}
bool _InsertR(Node*& root, const K& key)
{
if (root == nullptr)
{
root = new Node(key);
return true;
}
if (root->_key < key)
{
return _InsertR(root->_right, key);
}
else if (root->_key > key)
{
return _InsertR(root->_left, key);
}
else
{
return false;
}
}
bool _EraseR(Node*& root, const K& key)
{
if (root == nullptr) // 樹裏沒有
return false;
if (root->_key < key)
{
return _EraseR(root->_right, key);
}
else if (root->_key > key)
{
return _EraseR(root->_left, key);
}
else // 找到了,準備刪
{
Node* del = root;
if (root->_left == nullptr) // 1.左為空
{
root = root->_right;
}
else if (root->_right == nullptr) // 2.右為空
{
root = root->_left;
}
else // 3. 左右都不為空
{
Node* leftMax = root->_left;
while (leftMax->_right)
{
leftMax = leftMax->_right;
}
swap(root->_key, leftMax->_key);
return _EraseR(root->_left, key);
}
delete del;
return true;
}
}
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
private:
Node* _root;
};
void TestBSTree1()
{
int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
BSTree<int> t;
for (auto e : a)
{
t.InsertR(e);
}
t.InOrder();
t.EraseR(4);
t.InOrder();
t.EraseR(6);
t.InOrder();
t.EraseR(7);
t.InOrder();
t.EraseR(3);
t.InOrder();
for (auto e : a)
{
t.EraseR(e);
}
t.InOrder();
}
void TestBSTree2()
{
int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
BSTree<int> t;
for (auto e : a)
{
t.InsertR(e);
}
BSTree<int> t1(t);
t.InOrder();
t1.InOrder();
}四. 應用模型
1. key 的搜索模型
快速判斷在不在的場景
門禁系統、小區車輛出入系統 ……
2. key_value 的搜索模型
通過一個值找另一個值
商場的車輛出入系統、高鐵實名制車票系統 ……
namespace key_value
{
template<class K, class V>
struct BSTreeNode
{
BSTreeNode<K, V>* _left;
BSTreeNode<K, V>* _right;
K _key;
V _value;
BSTreeNode(const K& key, const V& value)
:_left(nullptr)
, _right(nullptr)
, _key(key)
, _value(value)
{ }
};
template<class K, class V>
class BSTree
{
typedef BSTreeNode<K, V> Node;
public:
BSTree()
:_root(nullptr)
{ }
void InOrder()
{
_InOrder(_root);
cout << endl;
}
Node* FindR(const K& key)
{
return _FindR(_root, key);
}
bool InsertR(const K& key, const V& value)
{
return _InsertR(_root, key, value);
}
bool EraseR(const K& key)
{
return _EraseR(_root, key);
}
private:
Node* _FindR(Node* root, const K& key)
{
if (root == nullptr)
return nullptr;
if (root->_key < key)
{
return _FindR(root->_right, key);
}
else if (root->_key > key)
{
return _FindR(root->_left, key);
}
else
{
return root;
}
}
bool _InsertR(Node*& root, const K& key, const V& value)
{
if (root == nullptr)
{
root = new Node(key, value);
return true;
}
if (root->_key < key)
{
return _InsertR(root->_right, key, value);
}
else if (root->_key > key)
{
return _InsertR(root->_left, key, value);
}
else
{
return false;
}
}
bool _EraseR(Node*& root, const K& key)
{
if (root == nullptr) // 樹裏沒有
return false;
if (root->_key < key)
{
return _EraseR(root->_right, key);
}
else if (root->_key > key)
{
return _EraseR(root->_left, key);
}
else // 找到了,準備刪
{
Node* del = root;
if (root->_left == nullptr) // 1.左為空
{
root = root->_right;
}
else if (root->_right == nullptr) // 2.右為空
{
root = root->_left;
}
else // 3. 左右都不為空
{
Node* leftMax = root->_left;
while (leftMax->_right)
{
leftMax = leftMax->_right;
}
swap(root->_key, leftMax->_key);
return _EraseR(root->_left, key);
}
delete del;
return true;
}
}
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_key << ":" << root->_value << endl;
_InOrder(root->_right);
}
private:
Node* _root;
};
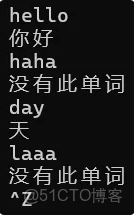
}拼寫檢查:讀取詞庫放到一顆搜索樹;讀取單詞,看在不在樹中,不在則拼寫錯誤
void TestBSTree1()
{
BSTree<string, string> dict;
dict.InsertR("hello", "你好");
dict.InsertR("tree", "樹");
dict.InsertR("apple", "蘋果");
dict.InsertR("day", "天");
string str;
while (cin >> str)
{
BSTreeNode<string, string>* ret = dict.FindR(str);
if (ret != nullptr)
{
cout << ret->_value << endl;
}
else
{
cout << "沒有此單詞" << endl;
}
}
}統計出現次數
void TestBSTree2()
{
string arr[] = { "蘋果", "西瓜", "蘋果", "西瓜", "蘋果",
"蘋果", "西瓜", "蘋果", "香蕉", "蘋果", "香蕉" };
BSTree<string, int> countTree;
for (auto& str : arr)
{
BSTreeNode<string, int>* ret = countTree.FindR(str);
if (ret == nullptr)
{
countTree.InsertR(str, 1);
}
else
{
ret->_value++;
}
}
countTree.InOrder();
}