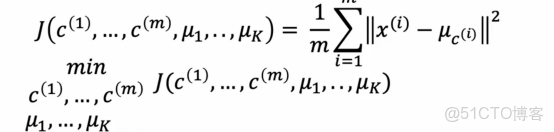目錄
- 摘要
- Abstract
- 一、優化目標
- 二、K-means算法的直觀理解
- 總結
摘要
今天深入學習了K-means算法的數學原理和優化過程。通過分析成本函數的構成,我理解了算法如何通過交替優化聚類分配和中心位置來最小化平方距離。具體來説,第一步是將每個點分配到最近的聚類中心,第二步是重新計算聚類中心為所屬點的平均值。這種迭代過程能保證成本函數持續下降直至收斂,讓我對算法的內在機制有了更清晰的認識。
Abstract
Today’s lesson delved into the mathematical foundation of the K-means algorithm and its optimization process. By examining the cost function composition, I learned how the algorithm minimizes squared distances through alternating optimization of cluster assignments and centroid positions. The first step assigns points to nearest centroids, while the second recalculates centroids as the mean of assigned points. This iterative process ensures consistent reduction of the cost function until convergence, providing deeper insight into the algorithm’s internal mechanics.
一、優化目標
在我們之前學習的過程中,我們看到了許多監督學習算法,它們使用訓練集,提出一個代價函數,然後使用梯度下降或者其他算法來優化這個代價函數,事實證明,我們在上一段視頻中,看到的K均值算法也在優化一個特定的代價函數,儘管它用來優化這個函數的算法不是梯度下降,其實是我們上一節學習的那個算法
讓我們看看K均值的代價函數是什麼,首先我們複習一下我們學的一些符號
ci是聚類的索引,ci是1到k的某個數字,表示當前分配給訓練樣本xi的聚類的索引
μk是聚類中心k的位置
μc(i)為樣本xi被分配的聚類的中心
例如如果我查看某個訓練樣本,然後我問,第10個訓練樣本被分配到的聚類中心的位置是什麼,這會給我一個從1到k的數字,告訴我們樣本10被分配到了紅色還是藍色或其他聚類中心,然後下標為c10的μ就是樣本x10被分配的聚類中心的位置,所以使用這個符號,可以讓我們寫出k-means正在最小化的成本函數,成本函數j是c1到cm的函數,這些是所有點分配到聚類中心的情況
這是平均值,所以除以1/m,從i等於1到m的綜合,每個訓練樣本xi之間的平方距離,這是xi和下標為ci的μ之間的平方距離,所以這裏的這個量,換句話説k-means的成本函數是每個訓練樣本xi與分配給該訓練樣本xi的聚類中心位置之間的平均平方距離,我們會測量x10和下標為c10的μ之間的距離,也就是x10被分配到的聚類中心,這將是我們在這裏的平均的項之一,事實證明k-means算法所做的是試圖找到點到聚類中心的分配,以及找到最小化平方距離的聚類中心的位置
二、K-means算法的直觀理解
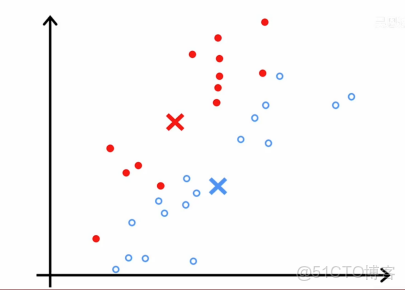
直觀上,這是我們在前面視頻中K-means算法運行一部分時看到的
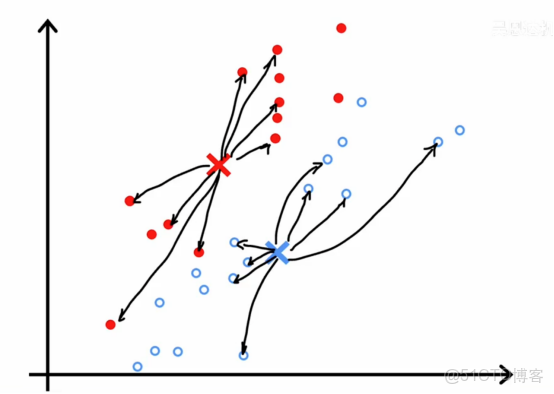
在這一步中,成本函數如果我們計算它,會是查看每一個藍點,測量這些距離並計算平方值,然後同樣查看每一個紅點,計算這些距離並取平方值
然後紅點和藍點所有這些差異的平方和平均值就是成本的值,在這種特定的參數配置下的k-means算法的代價值,,在每一步中,它會嘗試更新這個例子中的聚類分配c1到c30或者更新聚類中心μ1和μ2的位置,以繼續減少這個成本函數j
現在讓我們更深入的看看這個算法,以及為什麼算法試圖最小化這個成本函數j,在上面我們複製了剛剛我們説的成本函數
事實證明,k-means的第一部分,實際上是試圖更新c1到cm以儘可能最小化成本函數j同時保持μ1到μk固定,即移動聚類中心,實際上是試圖保持c1到cm固定,而更新μ1到μk儘可能地最小化成本函數或失真
在第一步,如果我們選擇c1到cm的值或保存特定的ci值以儘量減少這個,那麼是什麼使xi-μci儘可能的小呢
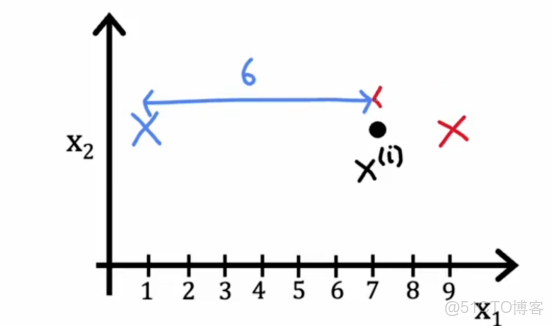
我們知道成本函數是訓練樣本xi和聚類中心位置之間的距離或者平方距離,所以如果我們想要最小化這個距離或這個平方距離,我們應該做的是將xi分配到最近的聚類中心,為了舉一個簡化的例子,比如説,聚類中心1和2
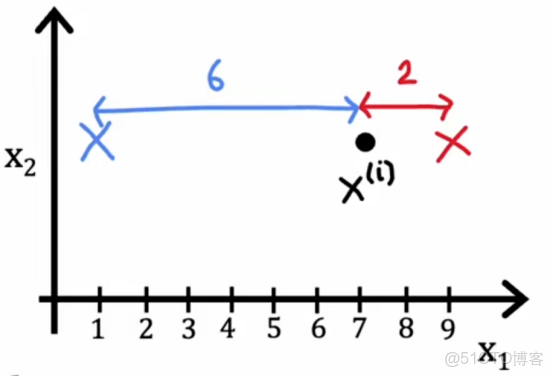
如果我們把它分配到聚類中心1,那麼這個平方距離將是這個大距離的平方
如果我們分配到聚類中心2,那麼這個平方的距離將是這個較小的平方距離
所以如果我們想要最小化這個項,我們會更加趨向把點分配到最近的聚類中心中去,這也正是上面算法所做的事情,因此,這就是為什麼在分配點到聚類中心的步驟中是選擇ci的值儘可能減少j,而不是改變μ1到μk,僅僅是選擇c1到cm的值以儘可能減小這些項
那麼k-means算法的第二步呢?
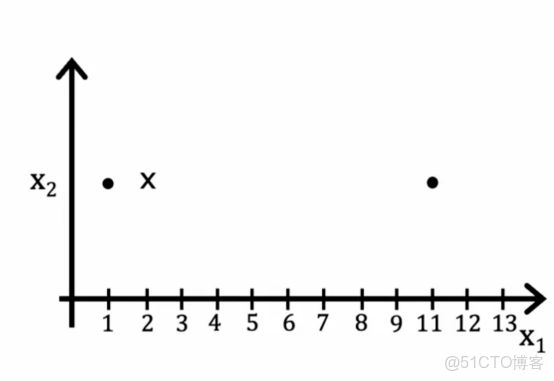
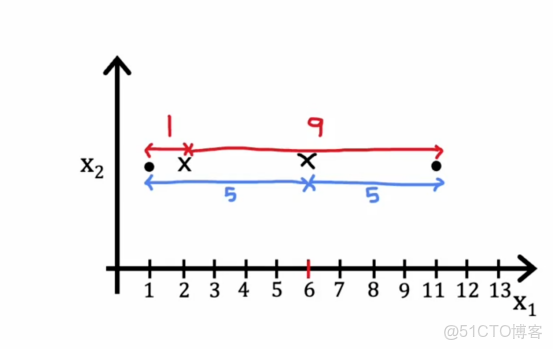
即移動聚類中心,事實證明,選擇μk為分配到它的點的平均值或均值是這些項μ的選擇,舉一個簡化的例子,假設我們有一個聚類只有兩個點分配給它,如下所示
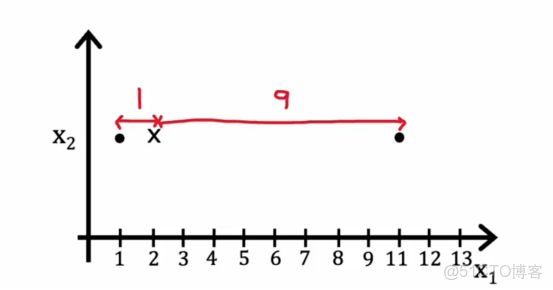
所以在這裏的聚類中心,距離的平均值將是這裏的距離1的平方加上這裏的距離,即9的平方
然後我們取這兩個數的平均值,所以結果是41,所以我們要移動到1/2*(1+11)中去後,那麼這裏的距離平均值是5和5
那麼得到的數值是25,遠遠小於42,實際上,我們可以試驗聚類中心的位置,並且可能發現取這個位置,在這兩個訓練示例之間的平均位置,因此k-means算法優化成本函數j的事實意味着它保證收斂,失真成本函數應該降低或者保持不變,但如果它不能減低或者保持不變,在最壞的情況下,如果它提高了,説明代碼出現問題了,它不應該永遠上升,因此k-means的每一步都在設置ci和μk以試圖減少成本,此外,如果成本函數停止下降,一旦有一次迭代爆出不變,這通常意味着k-means已經收斂,我們應該停止算法。
總結
今天的學習讓我真正理解了K-means算法背後的數學原理。之前只知道算法步驟,現在明白了每個步驟都是在優化那個平方距離的成本函數。最讓我印象深刻的是看到具體數值例子——當聚類中心移動到兩個點的中間位置時,成本從41降到了25,這種直觀的演示讓我理解了為什麼取平均值是最優選擇。算法保證收斂的特性也很重要,成本函數要麼下降要麼保持不變,這為我們判斷算法何時停止提供了明確依據。通過今天的學習,我不再只是機械地記住算法步驟,而是真正懂了為什麼這些步驟能夠有效工作,這對後續應用和調試算法都有很大幫助。