• 基礎知識預備

(1)無約束極值

求y的極值，對函數求導

，令導數等於0，則x=0就是它的極值點y=0。

同時，對

繪製圖形為U形曲線，找到這個曲線的凹凸點，可能為極值。

求z的極值，對函數求導就是求導

，令導數等於0，則x=0，y=0就是它的極值點z=0。

同時，對

繪製圖形為倒鐘形曲面，找到這個曲面的凹凸點，可能為極值。

簡單來説，無約束極值問題，可以通過求導(前提是可以求導)來找到極值。

(2)切線、法線

其導數

就是切線的斜率 。

對於點(3,9)，該點的切線方程y-9=6*(x-3)

注意跟下面的規律是一樣的因為

切線的斜率還等於

法線斜率與切線斜率乘積為-1，即若法線斜率和切線斜率分別用α、β表示，則必有α*β=-1。

該點的法線斜率為等於

。

一般化
曲面f(x,y,z)=0
記f(x,y,z)在點(a,b,c)的偏導數

那麼在點(a,b,c)處的切平面方程為

• 等式約束極值問題

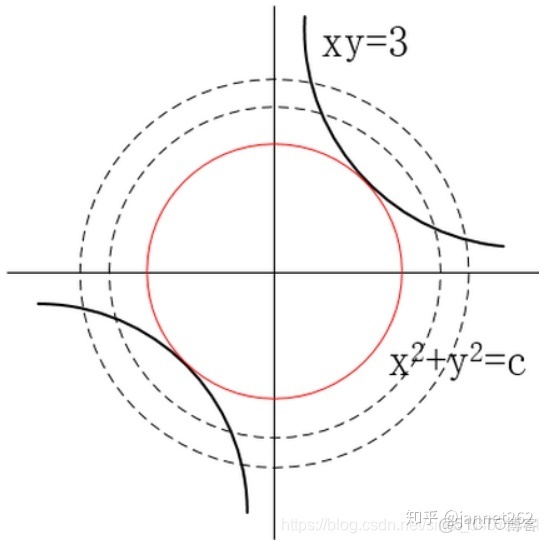
考慮約束極值問題：求雙曲線xy=3離原點最近的點？

令目標函數

，約束函數

，目標函數的等高線和約束曲線如下：

當目標函數與約束曲線相切時，可能取得最優值。當 f(x)與

相交時，在等高線f(x)的內外側一定存在更大或更小的等高線（目標值）。相切亦不一定保證是極值點，這與 f(x)和

的

凹凸性有關。f和

相切，則切線斜率相同，根據前面的基礎知識，也就是

也可以表示為

在本示例中

可求得解為

一般性，對於等式約束極值問題，定義輔助拉格朗日函數

(此處x代表多個變量)

分別對x和λ求偏導，並令各偏導為0，得

上述方程組，恰好給出了等式約束和最優解的必要條件。

• 一般化的約束極值問題

(1)原始問題

假設f(x),

是連續可微函數，考慮約束最優化問題

引入廣義拉格朗日函數

考慮x的函數

若某個i使得約束

,則令

,其餘的

等於0.

若某個j使得約束

,則讓

使得

，其餘的

等於0.

若滿足約束條件，則

,也就是

上述公式稱為廣義拉格朗日函數的極小極大問題

其對應的值

(2)對偶問題

上述公式稱為廣義拉格朗日函數的極大極小問題

其對應的值為

(3)原始問題和對偶問題的關係(證明省略)定理一：

定理二：在滿足一定的條件下，存在

使得

定理三：KKT條件

• 參考文獻
  李航《統計學習方法》