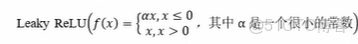目錄
摘要
激活函數
1.階躍函數
2.sigmod函數
3.Tanh函數
4.ReLu函數
代碼實踐
1.階躍函數
2.sigmod函數
3.tanh函數
4.ReLu函數
摘要
本篇文章學習尚硅谷深度學習教程,學習內容是激活函數的代碼部分包括階躍函數,sigmod函數,tanh函數,ReLu函數。
激活函數
下圖中,h(x)可以將輸入的信號加權總和轉換為輸出信號,被稱為激活函數。
激活函數是連接感知機和神經網絡的橋樑,在神經網絡中起着至關重要的作用。如果沒有激活函數,整個神經網絡就等效於單層線性變換,不論如何加深層數,總是存在與之等效的“無隱藏層的神經網絡”。激活函數必須是非線性函數,也正是激活函數的存在為神經網絡引入了非線性,使得神經網絡能夠學習和表示複雜的非線性關係。
1.階躍函數
下圖表示的h(x)就是最簡單的激活函數,它可以為輸入設置一個“閾值”;一旦超過這個閾值,就切換輸出(0或者1)。這種函數被稱為“階躍函數”。
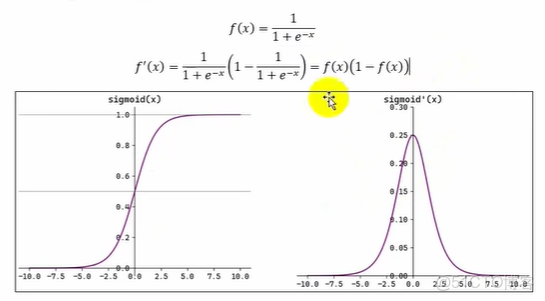
2.sigmod函數
函數表達式及其導函數表達式和函數圖像如下
Sigmoid(也叫 Logistic 函數)是平滑的、可微的,能將任意輸入映射到區間(0.1)。常用於二分類的輸出層。但因其涉及指數運算,計算量相對較高。Sigmoid 的輸入在[-6,6]之外時,其輸出值變化很小,可能導致信息丟失。Sigmoid 的輸出並非以0為中心,其輸出值均>0,導致後續層的輸入始終為正,可能影響後續梯度更新方向。Sigmoid 的導數範圍為(0,0.25),梯度較小。當輸入在[-6,6]之外時,導數接近 0,此時網絡參數的更新將會極其緩慢。使用Sigmoid作為激活函數,可能出現梯度消失(在逐層反向傳播時,梯度會星指數級衰減)。
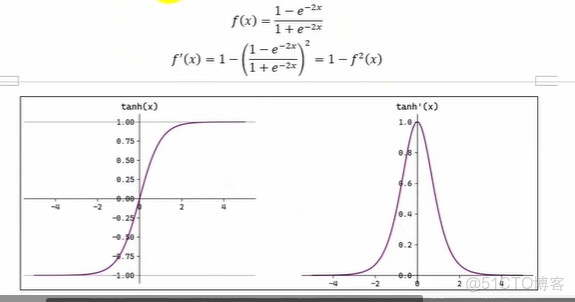
3.Tanh函數
在神經網絡中除了sigmod函數之外,tanh函數(雙曲正切函數)也比較常用。tanh函數在sigmod函數做了一些調整,tanh函數表達式及其導函數表達式和函數圖像如下
Tanh(雙曲正切)將輸入映射到區間(-1,1)。其關於原點中心對稱。常用在隱藏層。輸入在[-3,3]之外時,Tanh 的輸出值變化很小,此時其導數接近 0。Tanh 的輸出以0為中心,且其度相較於sigmoid 更大,收斂速度相對更快。但同樣也存在梯度消失現象。
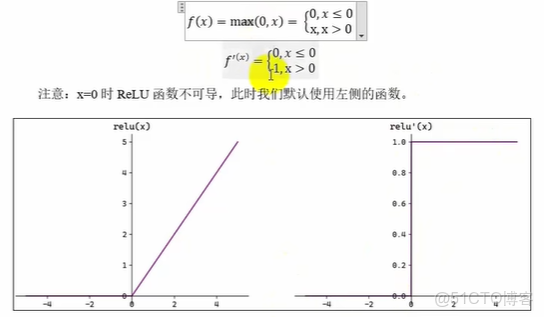
4.ReLu函數
ReLu函數表達式及其導函數表達式和函數圖像如下
ReLU(RectifedLimearUnit,修正線性單元)會將小於0的輸入轉換為0,大於等於0的輸入則保持不變。ReLU定義簡單,計算量小。常用於隱藏層。
ReLU 作為激活函數不存在梯度消失。當輸入小於0時,ReLU的輸出為0,這意味着在神經網絡中,ReLU激活的節點只有部分是“活躍”的,這種稀疏性有助於減少計算量和提高模型的效率。
當神經元的輸入持續為負數時,ReLU的輸出始終為0。這意味着神經元可能永遠不會被激活,從而導致“神經元死亡”問題。這會影響模型的學習能力,特別是如果大量的神經元都變成了“死神經元”。為解決此問題,可使用LeakyReLU 來代替 ReLU 作為激活函數。
在負數區域引入一個小的斜率來解決“神經元死亡”問題。
代碼實踐
學到的函數都比較常用,因此創建python工具包方便以後調用
1.階躍函數
接下來實現階躍函數,按上面的思路可以寫出一個簡單的階躍函數,只需要判斷即可
#階躍函數
def step_function0(x):
if x>0
return 1
else:
return 0但實際中並不一定輸入一個標量,往往是輸入一個向量。因此引用numpy庫中的array函數。
import numpy as np
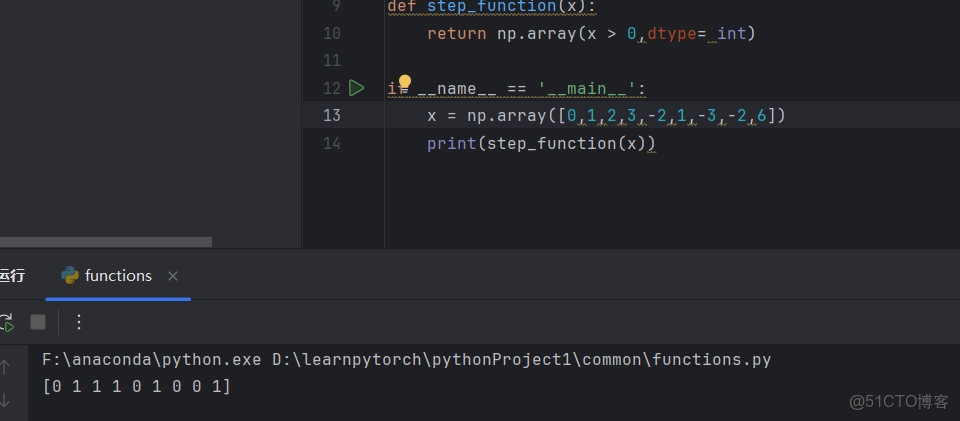
def step_function(x):
return np.array(x > 0,dtype= int)測試
2.sigmod函數
#sigmod函數
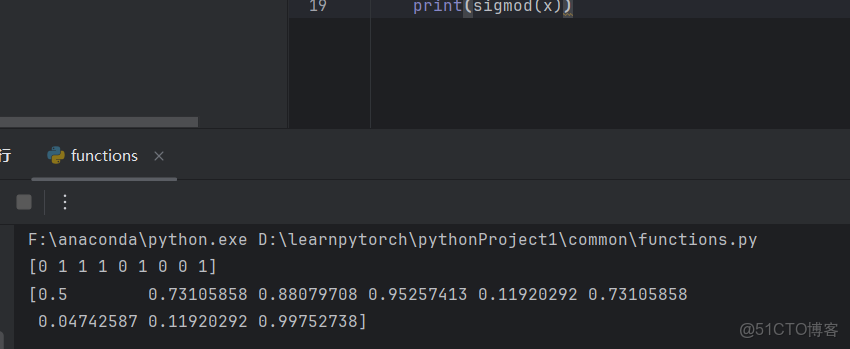
def sigmod(x):
return 1/(1+np.exp(-x))測試
3.tanh函數
在numpy中已經有tanh函數,直接調用即可
4.ReLu函數
#ReLu函數
def relu(x):
return np.maximum(0,x)測試