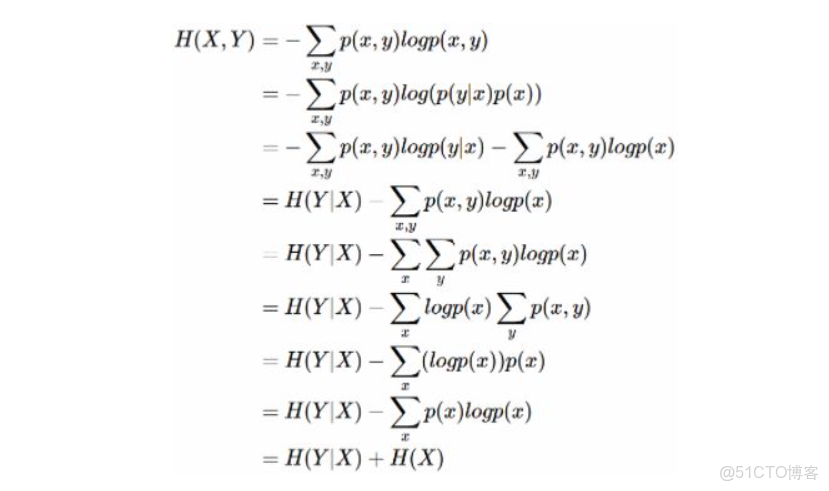1.信息量與信息熵
香農在他著名的論文”通信的數學原理“(A Mathematic Theory of Communication)中提出了”信息熵“的概念,解決了信息的度量問題,並且量化出信息的作用。
一條信息的信息量與其不確定性有着直接的關係。比如説,我們要搞清楚一件非常非常不確定的事,或是我們一無所知的事情,就需要了解大量的信息。相反,如果已對某件事瞭解較多,則不需要太多的信息就能把它弄清楚。從這個角度來看,可以認為,信息量就等於不確定性的多少(即與事件發生的概率有關)。當越不可能的事件發生了,我們獲取到的信息量就越大,越可能發生的事件發生了,我們獲取到的信息量就越小。
那麼如何量化信息量的度量呢?來看一個例子。2014年舉行了世界盃足球賽,大家都很關心誰會是冠軍。假如我錯過了看世界盃,賽後我問一個知道比賽結果的觀眾“哪支球隊是冠軍"?他不願意直接告訴我,而讓我猜,並且我每猜一次,他要收一元錢才肯告訴我是否猜對了,那麼我要掏多少錢才能知道誰是冠軍呢?我可以把球隊編上號,從1到32,然後提問:“冠軍球隊在1一16號中嗎?”假如他告訴我猜對了,我會接着問:“冠軍在1一8號中嗎?”假如他告訴我猜錯了,我自然知道冠軍隊在9一16號中。這樣只需要五次,我就能知道哪支球隊是冠軍。所以,誰是世界盃冠軍這條消息的信息量只值5塊錢。
當然,香農不是用錢,而是用“比特”(Bit)這個概念來度量信息量。一個比特是一位二進制數,在計算機中,一個字節就是8比特。在上面的例子中,這條消息的信息量是5比特。(如果有朝一日有64支球隊進入決賽階段的比賽,那麼“誰是世界盃冠軍"的信息量就是6比特,因為要多猜一次。)讀者可能已經發現,信息量的比特數和所有可能情況的對數函數log有關。(\(log_232=5,log_264=6\))
【信息量的定義】假設 \(X\) 是一個隨機變量,其取值集合為\(\chi\),概率分佈函數 \(p(x)=Pr(X=x), x\in\chi\),則定義事件 \(X=x_0\)
\[I(x_0)=-log(p(x_0)) \]
對於某隨機事件,每一種可能性可以計算出一個信息量,而熵用來表示所有信息量的期望。
有些讀者會發現實際上可能不需要猜五次就能猜出誰是冠軍,因為像西班牙、巴西、德國、意大利這樣的球隊奪得冠車的可能性比日本、南非、韓國等球隊大得多。因此,第一次猜測時不需要把32支球隊等分成兩個組,而可以把少數幾支最可能的球隊分成一組,把其他球隊分成另一組。然後猜冠軍球隊是否在那幾支熱門隊中。重複這樣的過程,根據奪冠概率對餘下候選球隊分組,直至找到冠軍隊。這樣,也許三次或四次就猜出結果。因此,當每支球隊奪冠的可能性(概率)不等時,“誰是世界盃冠軍”的信息量比5比特少。香農指出,它的準確信息量應該是
\[H=-(p_1logp_1+p_2logp_2+...+p_{32}logp_{32}) \]
其中,\(p_1,p_2,...,p_{32}\)分別是這32支球隊奪冠的概率。香農把它稱為“信息熵”(Entropy),一般用符號 \(H\)
\[0 \leq H \leq logn \]
【熵的定義】對於任意一個隨機變量 \(X\)(比如得冠軍的球隊),它的熵定義如下:
\[\begin{align*} H(X)&=-\sum _{x\in X}p(x)logp(x)\\ &= -\sum_{i=1}^n p(x_i)logp(x_i) \end{align*} \]
對於只有兩種取值的0-1分佈問題,熵的計算方法可以簡化為:
\[H(X)=-p(x)logp(x)-(1-p(x))log(1-p(x)) \]
將一維隨機變量分佈推廣到多維,可以得到聯合熵(joint entropy)為:
\[\begin{align*} H(X,Y)&=-\sum_{x,y}p(x,y)logp(x,y)\\ &=-\sum_{i=1}^n\sum_{j=1}^mp(x_i,y_i)logp(x_i,y_i) \end{align*} \]
變量的不確定性越大,熵也就越大,要把它搞清楚,所需信息量也就越大。
2.條件熵
有些時候,在戰爭中1比特的信息能抵過幹軍萬馬。在第二次世界大戰中.當納粹德國兵臨前蘇聯莫斯科城下時,斯大林在歐湖已經無兵可派,他們在西伯利亞的中蘇邊界卻有60萬大軍不敢使用,因為蘇聯人不知道德國的軸心國盟友日本當時的軍事策略是北上進攻前蘇聯,還是南下和美國開戰。如果是南下,那麼蘇聯人就可以放心大膽地從亞洲撤回60萬大軍增援莫斯科會戰。事實上日本人選擇了南下,其直接行動是後來的偷襲珍珠港,但是蘇聯人並不知驍。斯大林不能猜,因為猜錯了後果是很嚴重的。這個“猜“既是指扔鋼鏰兒似的卜卦,也包括主觀的臆斷。最後傳奇間諜佐爾格向莫斯科發去了信息量僅1比特卻價值無限的情報(信息):“日本將南下",於是前蘇聯就把西伯利亞所有的軍隊調往了歐洲戰場。後面的故事大家都知道了。
如果把這個故事背後的信息論原理抽象化、普遍化,可以總結如下:
一個事物(比如上面講到的日本內閣的戰略決定)內部會存有隨機性,也就是不確定性,假定為 \(U\),而從外部消除這個不確定性唯一的辦法是引入信息 \(I\),而需要引入的信息量取決於這個不確定性的大小,即 \(I>U\) 才行。當 \(I<U\)
\[U'=U-I \]
反之,如果沒有信息,任何公式或數字的遊戲都無法排除不確定性。幾乎所有的自然語言處理、信息與信號處理的應用都是一個消除不確定性的過程。
網頁搜索本質上就是要從大量(幾十億個)網頁中.找到和用户輸入的搜索詞最相關的幾個網頁。幾十億種可能性,當然是很大的不確定性 \(U\)。如果只剩下幾個網頁,就幾平沒有了不確定性了(此時 \(U'<<U\)),甚至是完全確定了(對於導航類搜索就是如此,第一條結果通常就是要找的網頁)。因此,網頁搜索本質上也是利用信息消除不確定性的過程。如果提供的信息不夠多,比如搜索詞是常用的關鍵詞,諸如“中國”、“經濟”之類的,那麼會有好多相關的結果,用户可能還是無從選擇,這時正確的做法是挖掘新的隱含信息,比如網頁本身的質量信息。如果這些信息還是不夠消除不確定性,不妨再問問用户。這就是相關搜索的理論基礎。不正確的做法是在這個關鍵詞上玩數字和公式的遊戲,由於沒有額外的信息引入,這種做法沒有效果,這就是很多做搜索質量的人非常辛苦卻很少有收穫的原因。最糟糕的做法是引入人為的假設,這和“蒙“沒什麼差別。其結果是似平滿足了個別用户的口味,但是對大部分用户來講,搜索結果反而變得更糟。合理利用信息,而非玩弄什麼公式和機器學習算法,是做好搜索的關鍵。
知道的信息越多,隨機事件的不確定性就越小。
這些信息,可以是直接針對我們要了解的隨機事件,也可以是和我們關心的隨機事件相關的其他(事件)的信息一一通過獲取這些相關信息也能幫助我們瞭解所關注的對象。比如自然語言的統計模型,其中的一元模型就是通過某個詞本身的概率分佈來清除不確定因素;而二元及更高階的語言模型則還使用了上下文的信息,那就能準確預測一個句子中當前的詞彙了。在數學上可以嚴格地證明為什麼這些”相關的“信息也能夠消除不確定性,為此,需要引入一個條件熵(Conditional Entropy)的概念。
假定 \(X\) 和 \(Y\) 是兩個隨機變量, \(X\) 是我們需要了解的。假定我們現在知道了 \(X\) 的隨機分佈 \(P(X)\),那麼也就知道了 \(X\)
\[H(X)=-\sum_{x\in X}P(x)logP(x) \]
那麼它的不確定性就是這麼大。現在假定我們還知道 \(Y\) 的一些情況,包括它和 \(X\) 一起出現的概率,在數學上稱為聯合概率分佈,以及在 \(Y\) 取不同值的前提下 \(X\)
【條件熵的定義】條件熵 \(H(X|Y)\) 定義為\(Y\)給定條件下\(X\)的條件概率的熵對\(Y\)的數學期望:
\[\begin{align*} H(X|Y)&=\sum_yp(y)H(X|Y=y)\\ &=-\sum_up(y)\sum_xp(x|y)logp(x|y)\\ &=-\sum_x\sum_yp(x,y)logp(y|x)\\ &=-\sum_{x,y}p(x,y)logp(y|x) \end{align*} \]
可以證明, \(H(X)\geq H(X|Y)\),即多了 \(Y\) 的信息之後,關於 \(X\) 的不確定性下降了。在統計語言模型中,如果把 \(Y\)
\[H(X|Y,Z)=-\sum_{x\in X,y\in Y,z\in Z}p(x,y,z)logp(x|y,z) \]
還可以證明, \(H(X|Y)\geq H(X|Y,Z)\)。也就是説,三元模型應該比二元好。
上述的等號什麼時候成立?等號成立説明增加了信息,不確定性卻沒有降低。如果我們獲取的信息與要研究的事物毫無關係,等號就成立。(下一節中介紹互信息時也會講到)
另外,還可以證明條件熵 \(H(X|Y)=H(X,Y)-H(Y)\)。證明如下:
舉個例子,比如環境温度是低還是高,和我穿短袖還是外套這兩個事件可以組成聯合概率分佈 \(H(X,Y)\),因為兩個事件加起來的信息量肯定是大於單一事件的信息量的。假設 \(H(X)\) 對應着今天環境温度的信息量,由於今天環境温度和今天我穿什麼衣服這兩個事件並不是獨立分佈的,所以在已知今天環境温度的情況下,我穿什麼衣服的信息量或者説不確定性是被減少了。當已知 \(H(X)\) 這個信息量的時候,\(H(X,Y)\) 剩下的信息量就是條件熵:\(H(Y|X)=H(X,Y)−H(X)\)
因此,可以這樣理解,描述 X 和 Y 所需的信息是描述 X 自己所需的信息,加上給定 X 的條件下具體化 Y 所需的額外信息。
用一句話概括這一節:信息的作用在於消除不確定性,自然語言處理的大量問題就是尋找相關的信息。
3.互信息
在上一節中提到,當獲取的信息和要研究的事物“有關係”時,這些信息才能幫助我們消除不確定性。如何量化地度量“相關性”,香農在信息論中提出了一個“互信息”(Mutual Information)的概念作為兩個隨機事件“相關性”的量化度量。
【互信息的定義】假定有兩個隨機事件 \(X\) 和 \(Y\),它們的互信息定義如下:
\[I(X;Y)=\sum_{x\in X,y\in Y}P(x,y)log\frac{P(x,y)}{P(x)P(y)} \]
這個互信息就是上節介紹的隨機事件 \(X\) 的不確定性(熵 \(H(X)\)),以及在知道隨機事件 \(Y\) 的條件下的不確定性(條件熵 \(H(X|Y)\))之間的差異,即
\[I(X;Y)=H(X)-H(X|Y) \]
即決策樹中的信息增益
所謂兩個事件相關的量化度量,就是在瞭解了其中一個 \(Y\) 的前提下,對消除另一個 \(X\)
互信息是一個取值在 \(0\) 到 \(min(H(X),H(Y))\)
- 當 \(X\) 和 \(Y\) 完全相關時,互信息的取值是 \(H(X)\),同時 \(H(X)=H(Y)\);
- 當二者完全無關時,互信息的取值是0。
即互信息越大,兩個隨機事件越相關。(越相關,越能消除另一個事件的不確定性)。
在自然語言處理中,兩個隨機事件,或者語言特徵的互信息是很容易計算的。只要有足夠的語料,就不難估計出互信息公式中的 \(P(X,Y),P(X)\) 和 \(P(Y)\) 三個概率,進而算出互信息。因此,互信息被廣泛用於度量一些語言現象的相關性。
機器翻譯中,最難的兩個問題之一是詞義的二義性(又稱歧義性,Ambiguation)問題。比如 Bush 可以是美國總統布什的名字,也可以是灌木叢。那麼如何正確地翻譯這些詞呢?
法一:用語法,分析語句,等等。-> 迄今為止沒有一種語法能很好地解決這個問題,Bush不論翻譯成人名還是灌木叢,都是名詞,在語法上沒有太大問題。
法二:加規則“總統做賓語時,主語得是一個人”。-> 要是這樣,語法規則就多得數不清,而且還有許多例外。
真正簡單卻非常實用的方法是使用互信息:
首先從大量文本中找出和總統布什一起出現的互信息量最大的一些詞,比如總統、美國、國會、華盛頓,等等。再用同樣的方法找出和灌木叢一起出現的互信息量最大的詞,比如土壤、植物、野生,等等。有了這兩組詞,再翻譯 Bush 時,看看上下文中哪類相關的詞多就可以了。
這種方法最初由吉爾(William Gale),丘奇(Kenneth Church)和雅讓斯基(David Yarowsky)提出。
4.相對熵(KL散度)
“相對熵”,在英語中是 \(Kullback-Leibler Divergence\)(KL散度)。
相對熵也用來衡量相關性,但和變量的互信息的不同,它用來衡量兩個取值為正數的函數的相似性。
【相對熵的定義】設p(x), q(x)是離散型隨機變量X的兩個概率分佈,p對q的相對熵是:
\[D_{KL}(p||q)=\sum_{x\in X} p(x)log\frac{p(x)}{q(x)} \quad\quad(4.1) \]
結論:
- 對於兩個完全相同的函數,它們的相對熵等於零。
- 相對熵越大,兩個函數的差異越大;反之,相對熵越小,兩個函數的差異越小。
- 對於概率分佈或概率密度函數,如果取值均大於零,相對熵可以度量兩個隨機分佈的差異性。
- \(D_{KL}(p||q)>=0\)
小結:相對熵可以用來衡量兩個概率分佈之間的差異。
如果對於同一個隨機變量 \(X\) 有兩個單獨的概率分佈 \(p(x)\) 和 \(q(x)\),我們可以使用KL散度來衡量這兩個分佈的差異。
維基百科對相對熵的定義:
In the context of machine learning, DKL(P||Q) is often called the information gain achieved if P is used instead of Q.
使用P來描述目標問題而不是Q,得到的信息增量。
例如,用P來表示樣本的真實分佈,Q表示模型所預測的分佈,那麼相對熵可以衡量Q還需要多少信息增量才能達到和P一樣完美的描述。
相對熵是不對稱的,即
\[D_{KL}(p||q) \neq D_{KL}(q||p) \]
這樣使用起來有時不是很方便,為了讓它對稱,詹森和香農提出一種新的相對熵的計算方法,將上面的不等式兩邊取平均,即
\[D_{JS}(p||q)=\frac{1}{2}[D_{KL}(p||q)+D_{KL}(q||q)] \]
相對熵最早是用在信號處理上。如果兩個隨機信號,它們的相對熵越小,説明這兩個信號越接近,否則信號的差異越大。後來研究信息處理的學者們也用它來衡量兩段信息的相似程度,比如説如果一篇文章是照抄或者改寫另一篇,那麼這兩篇文章中詞頻分佈的相對熵就非常小,接近於零。在Google自動問答系統中,我們採用了上面的詹森-香農度量來衡量兩個答案的相似性。
相對熵在自然語言處理中還有很多應用,比如用來衡量兩個常用詞(在語法和語義上)在不同文本中的概率分佈,看它們是否同義。另外,利用相對熵,還可以得到信息檢索中最重要的一個概念:詞頻率-逆向文檔頻率(TF-IDF)。
5. 交叉熵(cross entropy)
5.1 交叉熵的定義
對交叉熵的公式(4.1)變形可得到,
\[\begin{align*} D_{KL}(p||q)&=\sum_{x\in X}p(x)logp(x)-\sum_{x\in X}p(x)logq(x)\\ &=-H(p)+[-\sum_{x\in X}p(x)logq(x)] \end{align*} \]
等式的前一部分恰巧就是p的熵,等式的後一部分,就是交叉熵。
【交叉熵的定義】
\[H(p,q)=-\sum_{x\in X}p(x)logq(x) \]
所以有,\(D_{KL}(p||q)=H(p,q)-H(p)\).
在機器學習中,我們需要評估 label 和 prediction 之間的差距,可使用KL散度來度量,即 \(D_{KL}(y||\hat y)\),而由於KL散度的前一部分 \(-H(y)\)
小結:交叉熵可以用來計算學習模型分佈與訓練分佈之間的差異。交叉熵在邏輯迴歸的Sigmoid和Softmax函數中作為損失函數被廣泛使用。
5.2 交叉熵在機器學習中的應用
在監督式機器學習中,無論是迴歸問題還是分類問題,都少不了使用損失函數(Loss Function)。損失函數是用來估量模型的預測值 f(x) 與真實值 y 的不一致程度。若損失函數很小,表明機器學習模型與數據真實分佈很接近,則模型表現良好;若損失函數很大,表明機器學習模型與數據真實分佈差別較大,則模型表現不佳。訓練模型的主要任務就是使用優化方法來尋找損失函數最小時所對應的模型參數。
在線性迴歸中,常常使用 MSE(Mean Squared Error) 作為損失函數
\[loss = \frac{1}{2n}\sum_{i=1}^n(y_i-\hat{y_i})^2 \]
其中n代表樣本個數。
MSE在線性迴歸問題中比較好用,而在分類問題中最常用的是交叉熵損失函數。
5.2.1 交叉熵在單標籤場景下的使用
此處單標籤指每一個樣本只能有一個類別歸屬,例如一個圖像樣本,只能是貓或只能是狗。
定義損失函數:
\[loss = -\sum_{i=1}^my_ilog(\hat{y_i}) \]
上式為一個樣本的損失計算方法,其中,m代表m種類別。
對於二分類問題,單個樣本的損失計算可以簡化為:
\[loss = -ylog(\hat y) -(1-y)log(1-\hat y) \]
例如,有如下樣本:
對應的標籤和預測值為:
|
貓
|
青蛙
|
老鼠
|
|
|
label
|
0
|
1
|
0
|
|
prediction
|
0.3
|
0.6
|
0.1
|
那麼,
\[loss = -[0*log(0.3)+1*log(0.6)+0*log(0.1)]=-log(0.6)=0.737\]
對應一個batch的loss就是:
\[loss=-\frac{1}{n}\sum_{i=1}^n\sum_{j=1}^m y_{ij}log(\hat{y_{ij}})\]
其中 n 為當前batch的樣本數,m 為類別數。
5.2.2 交叉熵在多標籤場景下的應用
此處多標籤指一個樣本可能有多個類別歸屬,例如一個圖像樣本,可能同時包含一隻貓和一隻狗。
例如,有如下樣本:
對應的標籤和預測值:
|
貓
|
青蛙
|
老鼠
|
|
|
label
|
0
|
1
|
1
|
|
prediction
|
0.1
|
0.7
|
0.8
|
這裏的prediction不再是通過softmax計算的了,而是採用sigmoid, 將每一個節點的輸出歸一化到[0,1]之間。所有 predictions 的值加起來不一定等於1。每一個label都是獨立分佈的,相互之間沒有影響。所以交叉熵在這裏是單獨對每一個節點進行計算:
\[loss_貓=-0*log(0.1)-1*log(0.9)=-log(0.9)=0.152\\loss_蛙=-1*log(0.7)-0*log(0.3)=-log(0.7)=0.515\\loss_鼠=-1*log(0.8)-0*log(0.2)=-log(0.8)=0.322 \]
單個樣本的 loss 即為 \(loss=loss_貓+loss_蛙+loss_鼠\)。
每一個batch的loss就是:
\[loss=\sum_{i=1}^n\sum_{j=1}^m [-y_{ij}log(\hat y_{ij})-(1-y_{ij})log(1-\hat y_{ij})]\]
其中 n 為當前batch的樣本數,m 為類別數。
6. 補充
6.1 對數似然函數與交叉熵
邏輯迴歸中:log-likelihood等價於negative cross entropy,最大化log-likelihood等價於最小化cross entropy\(\rightarrow\)損失函數.
推導過程如下:
從極大似然的角度出發,預測類別的概率可以寫成:
\[P(y|x)=\hat y^y\cdot (1-\hat y)^{(1-y)}\]
其中 \(y\) 代表真實的標籤值,取值為1或0,\(\hat y\) 為預測概率值。
取log,可得到:
\[\begin{align*}logP(y|x)&=log(\hat y^y\cdot (1-\hat y)^{(1-y)})\\&=ylog(\hat y)+(1-y)log(1-\hat y) \end{align*} \]
可見,對數似然函數等價於負交叉熵,於是最大化對數似然函數等價於最小化交叉熵。
6.2 softmax與交叉熵
一句話概括:softmax把模型的原始輸出標準化成概率分佈;cross entropy 刻畫預測分類和真實結果之間的相似度。
多分類問題變為二分類問題時,softmax公式就轉化為sigmoid公式,損失函數由cross entropy轉化為binary cross entropy的形式。
6.3 關於softmax
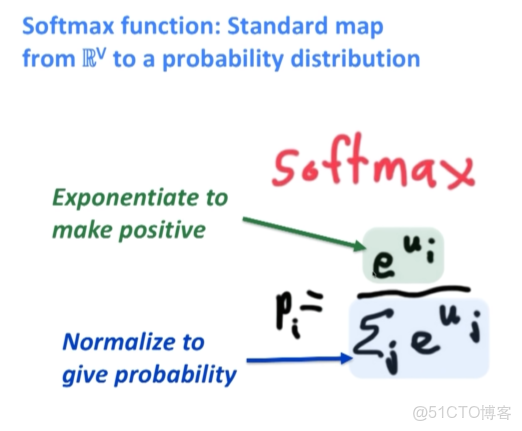
softmax把分類預測的輸出標準化,得到某個樣本點歸屬於各個類別的概率分佈。例如,歸屬於類別 \(j\)
\[p_j=softmax(z_j)=\frac{e^{z_j}}{\sum_{k=1}^K e^{z_k}}\]
其中 \(K\) 為類別數,\((z_1, z_2,..., z_K)\) 為模型的原始輸出。
(對比 sigmoid 函數:\(sigmoid(x)=\frac{1}{1+e^{-x}}\) )
這個結果滿足了概率分佈的標準化要求:在所有類別上的輸出概率都不小於0,且所有類別上的輸出概率和等於1。