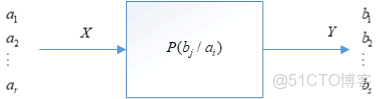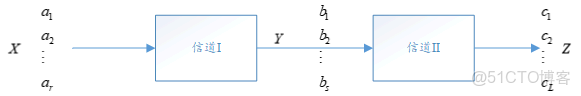交互信息量
信源的信息熵解決了定量估算信源每發出一個符號提供的平均信息量這個信源的核心問題,對於由信源、信道和信宿組成的通信系統來説,最根本的問題,還在於如何定量估算信宿收到消息後,從消息中獲取多少信息的問題,也就是信息傳輸問題。
信道的數學模型
考慮最簡單的信道,單符號離散信道,輸入端允許輸出\(r\)中不同的符號,輸出端相應輸出\(s\)中不同的符號,如下圖所示
\(p(b_j/a_i)\)這個條件概率體現了信道對輸入符號\(a_i\)的傳遞作用。不同的信道有不同的條件概率,因此條件概率\(p(b_j/a_i)\)可以稱為信道的傳遞概率。
我們可以使用傳遞概率矩陣來表示信道的傳遞特性
\[\begin{array}{l} \qquad \qquad \quad {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {b_1}\qquad \qquad {b_2}\qquad \ldots \qquad \quad {b_s}\\\\ [P] = \begin{array}{*{20}{c}} {{a_1}}\\\\ {{a_2}}\\\\ \vdots \\\\ {{a_r}} \end{array}\left( {\begin{array}{*{20}{c}} {p({b_1}/{a_1})}&{p({b_2}/{a_1})}& \ldots &{p({b_s}/{a_1})}\\\\ {p({b_1}/{a_2})}&{p({b_2}/{a_2})}& \ldots &{p({b_s}/{a_2})}\\\\ \vdots & \vdots & \ldots & \vdots \\\\ {p({b_1}/{a_r})}&{p({b_2}/{a_r})}& \ldots &{p({b_s}/{a_r})} \end{array}} \right) \end{array} \]
交互信息量
怎麼計算兩個事件之間傳遞的信息量,或者説怎麼計算信宿接收到的信息量,我們可以這麼理解,我們把對不確定性大小的消除理解為接收到的信息量,消除了多少不確定性就代表接收到了多少的信息。那麼消除的不確定的表達式是什麼呢?應該是信宿在接收前對信源發出符號的不確定性減去在接收到符號後對信源還保留的不確定性的大小。那麼我們就可以定義交互信息量了,簡稱互信息。
互信息表示的兩個事件之間傳遞的信息量,我們定義為
\[I(x;y) = I(x) - I(x|y) \]
上面的定義可以這麼理解:對於一個通信系統,\(I(x)\)表示接收到\(x\)前,信宿對信源發送\(x\)的不確定性,\(I(x|y)\)表示接收到符號後,推測發送的是\(x\)的還保留的不確定性,二者之差就表示信宿消除的不確定性,也就表示信宿所獲得的信息量。
根據上面的表達式,我們可以推出\(I(x;y)\)的表達式為
\[I(x;y) = I(x) - I(x|y)= -logP(x) + logP(x|y) = log\cfrac{P(x|y)}{p(x)} = log\cfrac{p(x,y)}{p(x)p(y)} = I(x) + I(y) - I(xy) \]
從另一個角度理解\(I(x|y)\)
\[I(x;y) = I(x) - I(x|y) \]
\(I(x;y)\)表示信宿獲得的信息量,\(I(x)\)表示發送方發送的信息量,那麼$I(x|y)= I(x) - I(x;y) $就可以看做是在符號傳輸過程中損失的信息量。
反向信道
在已知先驗概率\(p(a_i)\)以及信道傳遞概率\(p(b_j/a_i)\)的情況下,我們可以很簡單的計算出後驗概率\(p(a_i/b_j)\)
\[p(a_i/b_j) = \cfrac{p(a_ib_j)}{\sum\limits_{i=1}^{r}p(a_i)p(b_j/a_i)} = \cfrac{p(a_i)p(b_j/a_i)}{\sum\limits_{i=1}^{r}p(a_i)p(b_j/a_i)} \]
那麼\(p(a_i/b_j)\)可以看做是信源是\(Y\),信宿為\(X\)的傳遞概率,相應的信道我們稱之為反向信道,相應的反向信道傳遞概率矩陣為
\[\begin{array}{l} \qquad \qquad \quad {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {a_1}\qquad \qquad {a_2}\qquad \ldots \qquad \quad {a_r}\\ [P] = \begin{array}{*{20}{c}} {{b_1}}\\\\ {{b_2}}\\\\ \vdots \\\\ {{b_s}} \end{array}\left( {\begin{array}{*{20}{c}} {p({a_1}/{b_1})}&{p({a_2}/{b_1})}& \ldots &{p({a_r}/{b_1})}\\\\ {p({a_1}/{b_2})}&{p({a_2}/{b_2})}& \ldots &{p({a_r}/{b_2})}\\\\ \vdots & \vdots & \ldots & \vdots \\\\ {p({a_1}/{b_s})}&{p({a_2}/{b_s})}& \ldots &{p({a_r}/{b_s})} \end{array}} \right) \end{array} \]
那麼
\[I(y;x) = I(y) - I(y|x) = -logP(y) + logP(y|x) = log\cfrac{P(y|x)}{p(y)} = log\cfrac{p(x,y)}{p(y)p(x)} = I(x) + I(y) - I(xy) \]
我們可以得到
\[I(x;y) = I(y;x) \]
所以不論是\(X\)向\(Y\)傳遞信息,還是\(Y\)向\(X\)傳遞信息,它們傳遞的信息量是相同的,這也是它們為什麼叫做互信息的原因。
條件互信息量
考慮三個事件\(x,y,z\),條件互信息量即在其中一個事件發生的情況下,另外兩個事件所交互的信息量,根據互信息量的定義,條件互信息量應定義為
\[I(x;y|z) = I(x|z) - I(x|yz) \]
我們可以得到條件互信息量的表達式
\[I(x;y|z) = \log{}\cfrac{p(x|yz)}{p(x|z)} =\log{}\cfrac{p(x,y|z)}{p(x|z)p(y|z)} = I(x|z) + I(y|z) - I(xy|z) \]
同理,我們可以得到
\[I(x;y|z) = I(y;x|z) \]
平均交互信息量
如何計算信源\(X\)向信宿\(Y\)傳遞的信息的大小,或者説怎麼計算信宿接收到信息的大小。同上,我們把信宿\(Y\)接收到的信息大小也定義為對信源\(X\)不確定性的消除。那麼同理我們可以很快的得出交互信息量的表達式
\[I(X;Y) = H(X) - H(X/Y) = H(X) + H(Y) - H(XY) \]
所表達的意思同上。
同樣的我們可以得到
\[I(Y;X) = H(Y) - H(Y/X) = H(X) + H(Y) - H(XY) \]
所以我們得到
\[I(X;Y) = I(Y;X) \]
平均互信息量的性質
非負性
考慮
\[I(X;Y) = \sum_{i = 1}^r\sum_{j = 1}^sp(a_ib_j)\log{}\cfrac{p(a_ib_j)}{p(a_i)p(b_j)} \]
則
\[\begin{aligned} -I(X;Y) &= \sum_{i = 1}^r\sum_{j = 1}^sp(a_ib_j)\log{}\cfrac{p(a_i)p(b_j)}{p(a_ib_j)} \\\\ &\leq \log{}\sum_{i = 1}^r\sum_{j = 1}^sp(a_ib_j)\cfrac{p(a_i)p(b_j)}{p(a_ib_j)} \\\\ &= \log{} 1 \\\\ &= 0 \end{aligned} \]
所以
\[I(X;Y) \geq 0 \]
上面利用了\(\log\)函數是上凸函數的性質,即
\[\log{}\sum_{i=1}^n p_ix_i \geq \sum_{i=1}^n p_i\log{}x_i \]
其中
\[\sum_{i=1}^np_i = 1 \]
當前僅當兩個隨機變量\(X,Y\)統計獨立時,才有\(I(X;Y)=0\)。
極值性
我們知道,互信息量的表達式為
\[\begin{aligned} I(X;Y) &= H(X) - H(X|Y) \\ &= H(Y) - H(Y|X) \end{aligned} \]
並且
\[H(X|Y) = \sum_{i = 1}^r\sum_{j = 1}^s p(a_ib_j)\log{}\cfrac{1}{p(a_i|b_j)} \\ \]
由於\(0\leq p(a_ib_j)\leq 1, 0\leq p(a_i|b_j) \leq 1\),所以
\[p(a_ib_j)\log{}\cfrac{1}{p(a_i|b_j)} \geq 0 \]
所以我們得到
\[H(X|Y) \geq 0 \]
同理,我們也可以得到
\[H(Y|X) \geq 0 \]
所以有
\[I(X;Y) = H(X) - H(X|Y) \leq H(X) \\ I(Y;X) = H(Y) - H(Y|X) \leq H(Y) \]
這表示\(I(X;Y)\)有最大值,是為極值性。
那麼在什麼條件下取得極值呢? 首先看
\[I(X;Y) = H(X) - H(X|Y) \]
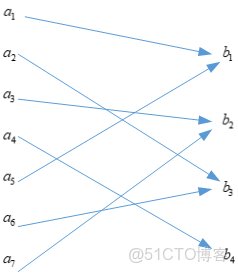
明顯,當\(H(X|Y) = 0\)時,\(I(X;Y)\)可以取得極大值\(H(X)\),所以\(H(X|Y)\)在什麼條件下取值為\(0\)呢? 要回答這個問題,可以從\(H(X|Y)\)的物理意義出發,\(H(X|Y)\)表示信宿接收到符號後,對信源發送什麼符號的猜測,表示猜測的不確定性的大小,如果\(H(X|Y)\)為\(0\)則表示,對信源發出符號不確定性為\(0\),即可以完美的知道信源發出的符號是什麼,所以信道模型應該如下
這樣的話,當接收到符號後,可以推測出信源發出的是什麼,相應的信道轉移概率矩陣為
\[\begin{array}{*{20}{l}} {\quad \quad \quad \qquad \quad {b_1}\qquad \quad {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {b_2}\qquad \qquad {b_3}\qquad \qquad {b_4}\qquad \qquad {b_5}\qquad \qquad {b_6}\qquad \qquad {b_7}}\\\\ {[P] = \begin{array}{*{20}{c}} {{a_1}}\\\\ {{a_2}}\\\\ {{a_3}}\\\\ {{a_4}} \end{array}\left( {\begin{array}{*{20}{c}} {p({b_1}/{a_1})}&{p({b_2}/{a_1})}&0&0&0&0&0\\\\ 0&0&{p({b_3}/{a_2})}&{p({b_4}/{a_2})}&{p({b_5}/{a_2})}&0&0\\\\ 0&0&0&0&0&{p({b_6}/{a_3})}&0\\\\ 0&0&0&0&0&0&{p({b_7}/{a_4})} \end{array}} \right)} \end{array} \]
我們觀察,可以發現每一列只有一個非零值。所以我們可以得到這麼一個結論,當轉移概率矩陣的每一列只有一個非零值,\(I(X;Y)\)可以取到最大值為\(H(X)\)。
同理,當\(H(Y|X)\)為\(0\)時,應該有如下的信道模型
對應的信道轉移概率矩陣為
\[\begin{array}{l} \qquad \quad \quad\,\,{\mkern 1mu} {\mkern 1mu} {b_1}\,\,\,\, {b_2}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu}\,\, {b_3}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu}\, {b_4}\\\\ P = \begin{array}{*{20}{c}} {{a_1}}\\\\ {{a_2}}\\\\ {{a_3}}\\\\ {{a_4}}\\\\ {{a_5}}\\\\ {{a_6}}\\\\ {{a_7}} \end{array}\left( {\begin{array}{*{20}{c}} 1&0&0&0\\\\ 0&0&1&0\\\\ 0&1&0&0\\\\ 0&0&0&1\\\\ 1&0&0&0\\\\ 0&0&1&0\\\\ 0&1&0&0 \end{array}} \right) \end{array} \]
觀察該信道轉移概率矩陣的特點,該矩陣只由\(0\)和\(1\)組成,所以我們可以得到這個結論,當轉移概率矩陣中所有元素,要麼是\(0\),要麼為\(1\)時,則\(I(X;Y)\)取得最大值,最大值為\(H(Y)\)。
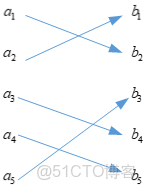
考慮這麼一種特殊情形,是上面兩種情況的結合,即信道轉移概率矩陣的每一列只有一個非零元素,並且該矩陣只由\(0\)和\(1\)組成,那麼我們可以得到轉移概率矩陣為
\[P = \left( {\begin{array}{*{20}{c}} 0&1&0&0&0\\\\ 1&0&0&0&0\\\\ 0&0&0&1&0\\\\ 0&0&0&0&1\\\\ 0&0&1&0&0 \end{array}} \right) \]
對應的信道模型為
此時信道模型是一一對應的,並且此時\(I(X;Y)\)取得最大值為\(H(X) = H(Y)\)。
不增性
在實際通信系統中,常需要對信道傳輸的數據作適當處理。若把數據處理裝置亦看做是一個信道,這就由兩個信道串接,組成了一個串聯信道:
則
\[I(X;Z) \leq I(X;Y) \]
具體的證明可以查閲書本,這裏只講表示的意義,\(I(X;Z)\)表示\(Z\)獲得信息量,\(I(X;Y)\)表示\(Y\)獲得的信息量,上面的關係式表示,在經過信道\(II\)後,即經過數據處理後(不論怎麼處理),信息都有所損失,這就是數據處理定理。即不論怎麼處理數據,最好的情況是沒有信息的損失,但是一定不會有信息的增加。
上式取等號當且僅當信道\(II\)是一個可逆信道時,即\(Z\)經過信道\(II\)的可逆信道後,可以完整的將\(Y\)恢復出來,這時等號成立:
\[I(X;Z) = I(Y;Z) \]
上凸性
互信息量的表達式為
\[\begin{aligned} I(X;Y) &= \sum_{i = 1}^{r}\sum_{j = 1}^{s}p(a_{i}b_{j})\log{}\cfrac{p(b_j/a_i)}{p(b_j)} \\\\ &= \sum_{i = 1}^{r}\sum_{j = 1}^{s}p(a_{i})p(b_j/a_i)\log{}\cfrac{p(b_j/a_i)}{\sum\limits_{i=1}^rp(a_i)p(b_j/a_i)} \\\\ &= I(p(a_i),p(b_j/a_i)) \end{aligned} \]
可以發現,互信息量是先驗概率和轉移概率的函數。
當信道轉移概率\(p(b_j/a_i)\)確定時,此時\(I(X;Y)\)是關於\(p(a_i)\)的函數,在數學上可以證明,\(I(p(a_i))\)是上凸函數,即存在最大值。所以當信道轉移概率確定時,即在給定信道的條件下,存在一種信源分佈,使得\(I(X;Y)\)最大,這個值是對給定信道的情況下最多能夠傳輸的信息量,所以我們定義這個量為信道容量\(C\),即
\[C = max\{I(X;Y)\} \]