數據結構之二叉搜索樹、AVL自平衡樹詳情 - 子樹,遞歸,輔助函數,HarmonyOS,後端開發雲端創新者博客

文章目錄

引言：當“秩序”走向“極端”
一、平衡的“標尺”：平衡因子 (BF)
二、“撥亂反正”：AVL樹的四種旋轉

1. LL 型（左左）：右旋
2. RR 型（右右）：左旋
3. LR 型（左右）：先左旋再右旋
4. RL 型（右左）：先右旋再左旋

三、AVL樹的C語言實現

1. 結構設計
2. 核心輔助函數
3. 旋轉操作 (核心)
4. 插入操作 (帶平衡調整)
5. 刪除操作 (帶平衡調整)

四、總結：嚴格平衡的“代價”

引言：當“秩序”走向“極端”

在上一篇文章中，我們見證了二叉搜索樹（BST）的強大——它依靠“左小右大”的秩序，在平均情況下提供了 O(log n) 的高效操作。

然而，這份“秩序”是脆弱的。如果我們按順序 (1, 2, 3, 4, 5) 插入數據，會發現了一個大大的問題：，BST會退化成一條單鏈表，所有操作的效率也隨之退化到 O(n)。我們精心構建的“秩序”反而成了我們的枷鎖。

數據結構之二叉搜索樹、AVL自平衡樹_遞歸

BST退化成鏈表

為了讓操作效率始終保持在O(logn)，兩位蘇聯數學家 Adelson-Velsky 和 Landis 在1962年提出了一種嚴格的自平衡結構——AVL樹。

一、平衡的“標尺”：平衡因子 (BF)

AVL 樹的實現，就是在二叉搜索樹的基礎上，增加了一條“鐵律”：
樹中任意一個節點的左、右子樹的高度差（平衡因子），其絕對值不能超過1。

平衡因子 (BF) = 左子樹高度 - 右子樹高度

因此，在一個合法的 AVL 樹中，每個節點的平衡因子 BF 只能是：

1：左子樹比右子樹高1層（左高）。
0：左、右子樹等高。
-1：右子樹比左子樹高1層（右高）。

一旦某個節點的 BF 變成了 2 或 -2，就説明樹“失衡”了，必須立刻進行調整。

二、“撥亂反正”：AVL樹的四種旋轉

AVL 樹保持平衡的秘訣，就在於它在插入或刪除後，會沿着路徑回溯，檢查路徑上所有祖先節點的平衡因子。一旦發現失衡（BF 變為 ±2），就會立即啓動“旋轉”操作，進行局部重構，使子樹恢復平衡。

旋轉的本質是在保持BST“左小右大”性質（即中序遍歷不變）的前提下，通過指針的挪移來降低子樹的高度。

根據新節點插入的位置，有四種失衡情況：

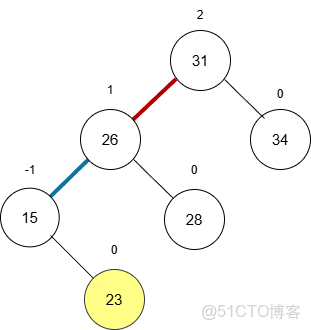
1. LL 型（左左）：右旋

成因：新節點插入到了“失衡節點”31的左子樹的左側。
表現：31 的 BF 變為 2，31 的左孩子 26 的 BF 變為 1。

數據結構之二叉搜索樹、AVL自平衡樹_輔助函數_02

調整：對 26 進行右旋。

26 提拔為新的根。
31 降級為 26 的右孩子。
26 原來的右子樹（28）“過繼”給 31，成為 31 的左子樹。

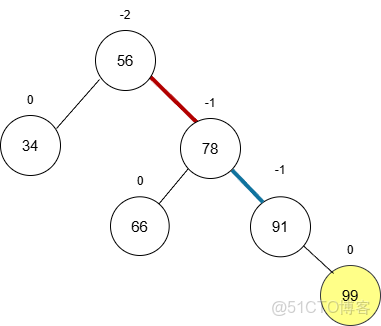
2. RR 型（右右）：左旋

成因：新節點插入到了“失衡節點”56 的右子樹的右側。
表現：56 的 BF 變為 -2，56 的右孩子 78 的 BF 變為 -1。

數據結構之二叉搜索樹、AVL自平衡樹_遞歸_03

調整：對 56 進行左旋。

78 提拔為新的根。
56 降級為 78 的左孩子。
78 原來的左子樹（66）“過繼”給 56，成為 56 的右子樹。

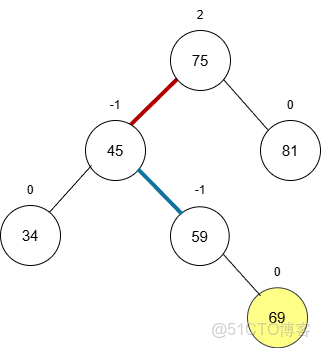
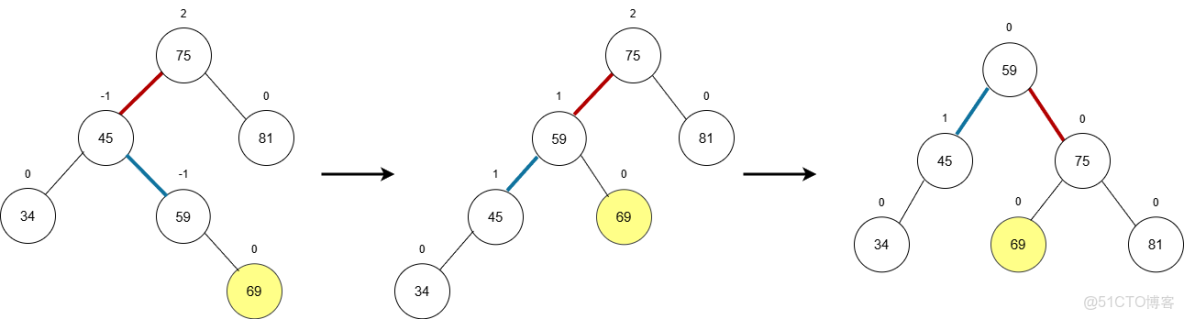
3. LR 型（左右）：先左旋再右旋

成因：新節點插入到了“失衡節點”75 的左子樹的右側。
表現：75 的 BF 變為 2，75的左孩子 45 的 BF 變為 -1。

數據結構之二叉搜索樹、AVL自平衡樹_輔助函數_04

調整：

對 45 (75的左孩子) 進行一次左旋，將其轉化為 LL 型。
對 75 (失衡節點) 進行一次右旋。

數據結構之二叉搜索樹、AVL自平衡樹_子樹_05

4. RL 型（右左）：先右旋再左旋

成因：新節點插入到了“失衡節點”45 的右子樹的左側。
表現：45 的 BF 變為 -2，A 的右孩子 75 的 BF 變為 1。
調整：

對 75 (45的右孩子) 進行一次右旋，將其轉化為 RR 型。
對 45 (失衡節點) 進行一次左旋。

三、AVL樹的C語言實現

1. 結構設計

每個節點必須額外存儲 height（高度）字段，平衡因子 BF 可以通過左右子樹的 height 動態計算得出。

#include <stdio.h>
  #include <stdlib.h>
    typedef int Element;
    // 平衡二叉樹的節點結構
    typedef struct _avl_Node
    {
    Element data;
    struct _avl_Node *left, *right;
    int height; // 節點高度 (以該節點為根的子樹的最大高度)
    } AVLNode;
    // 平衡二叉樹的樹頭結構
    typedef struct
    {
    AVLNode *root;
    int count;
    } AVLTree;

2. 核心輔助函數

// 獲取節點高度（NULL節點高度為0）
static int h(AVLNode *node) {
if (node == NULL) {
return 0;
}
return node->height;
}
// 比較並取更大值
static int maxNum(int a, int b) {
return (a > b) ? a : b;
}
// 計算平衡因子
static int getBalance(const AVLNode *node) {
if (node == NULL) {
return 0;
}
return h(node->left) - h(node->right);
}
// 創建一個新節點
static AVLNode *createAVLNode(Element data, AVLTree* tree) {
AVLNode *node = (AVLNode*)malloc(sizeof(AVLNode));
if (node == NULL) {
return NULL;
}
node->data = data;
node->left = node->right = NULL;
node->height = 1; // 新節點高度默認為1
tree->count++;
return node;
}

3. 旋轉操作 (核心)

/* 左旋操作
*      px              px
*      |               |
*      x               y
*    /  \    --->    /  \
*   lx   y          x    ry
*       / \        / \
*     ly  ry     lx  ly
*/
static AVLNode *leftRotate(AVLNode *x)
{
AVLNode* y = x->right;
x->right = y->left;
y->left = x;
// 更新高度（必須先更新x，再更新y）
x->height = maxNum(h(x->left), h(x->right)) + 1;
y->height = maxNum(h(y->left), h(y->right)) + 1;
return y;
}
/*      py              py
*      |               |
*      y               x
*    /  \    --->    /  \
*   x    ry         lx   y
*  / \                  / \
* lx  rx               rx  ry
*/
static AVLNode *rightRotate(AVLNode *y)
{
AVLNode* x = y->left;
y->left = x->right;
x->right = y;
// 更新高度（必須先更新y，再更新x）
y->height = maxNum(h(x->left), h(x->right)) + 1;
x->height = maxNum(h(y->left), h(y->right)) + 1;
return y;
}

4. 插入操作 (帶平衡調整)

AVL 樹的插入，就是在 BST 插入的遞歸回溯過程中，增加了檢查平衡並執行旋轉的步驟。

// 插入的遞歸輔助函數
static AVLNode *insertAVLNode(AVLTree* tree, AVLNode *node, Element e) {
// 1. 遞歸的初始化位置
if (node == NULL) {
return createAVLNode(e, tree);
}
// 遞的過程
if (e < node->data) {
  node->left = insertAVLNode(tree, node->left, e);
  } else if (e > node->data) {
  node->right = insertAVLNode(tree, node->right, e);
  } else {
  return node; // 不允許插入重複值
  }
  // 2. 此時的代碼，已經進入到歸的過程，更新這條路徑上節點高度，同時檢測平衡因子
  // 2.1 歸過程中的節點高度的更新
  updateHeight(node);
  // 2.2 計算當前節點的平衡因子
  int balance = getBalance(node);
  // 3. 檢查是否失衡，並執行相應旋轉
  if (balance > 1) {
  // 左邊的高度大了
  if (e > node->left->data) {
  // LR
  node->left = leftRotate(node->left);
  }
  // LL
  return rightRotate(node);
  }
  if (balance < -1){
  if (e < node->right->data) {
    // RL
    node->right = rightRotate(node->right);
    }
    // RR
    return leftRotate(node);
    }
    return node;
    }
    // 對外接口：插入
    void insertAVLTree(AVLTree* tree, Element data) {
    if (tree) {
    tree->root = insertAVLNode(tree, tree->root, data);
    }
    }

5. 刪除操作 (帶平衡調整)

刪除操作與插入類似，但在刪除節點後（尤其是度為2的節點，替換前驅/後繼後），也需要在回溯路徑上檢查平衡性並進行旋轉。

// 刪除的遞歸輔助函數
static AVLNode *deleteAVLNode(AVLTree *tree, AVLNode *node, Element e) {
if (node == NULL) {
return NULL; // 未找到
}
// 1. 找到要刪除的節點
if (e < node->data) {
  node->left = deleteAVLNode(tree, node->left, e);
  } else if (e > node->data) {
  node->right = deleteAVLNode(tree, node->right, e);
  } else {
  // 找到了,執行刪除
  AVLNode *tmp;
  if (node->left == NULL || node->right == NULL) {
  tmp = node->left ? node->left : node->right;
  if (tmp == NULL) {
  // 度為0，直接刪除
  tree->count--;
  free(node);
  return NULL;
  }
  // 度為1，將tmp的值總結替換成node
  node->data = tmp->data;
  node->left = tmp->left;
  node->right = tmp->right;
  tree->count--;
  free(tmp);
  } else {
  // 度為2的點，找前驅節點
  tmp = node->left;
  while (tmp->right) {
  tmp = tmp->right;
  }
  node->data = tmp->data;
  node->left = deleteAVLNode(tree, node->left, tmp->data);
  }
  }
  // 2.歸的過程中，更新平衡因子
  updateHeight(node);
  // 3. 計算平衡因子
  int balance = getBalance(node);
  // 4. 檢查並執行旋轉 (邏輯與插入時類似，但判斷條件略有不同)
  if (balance > 1) {
  if (getBalance(node->left) < 0) {
  node->left = leftRotate(node->left);
  }
  return rightRotate(node);
  }
  if (balance < -1) {
  if (getBalance(node->right) > 0) {
  node->right = rightRotate(node->right);
  }
  return leftRotate(node);
  }
  return node;
  }
  // 對外接口：刪除
  void deleteAVLTree(AVLTree* tree, Element e) {
  if (tree) {
  tree->root = deleteAVLNode(tree, tree->root, e);
  }
  }

四、總結：嚴格平衡的“代價”

AVL 樹以其極其嚴格的平衡策略（BF 絕對值不超過1），確保了無論數據如何插入，樹的高度始終被“壓”在 O(log n) 級別，提供了極其穩定的 O(log n) 查找效率。

但這份“嚴格”是有代價的：

優點：查找效率極高且非常穩定，非常適合查找密集型的應用。
缺點：為了維持這種嚴格平衡，插入和刪除時可能需要頻繁的旋轉（最多O(log n)次旋轉），這使得其“寫”操作的開銷比 BST 更大。

至此，我們對“樹”這種層級結構的探索，已經達到了一個相當的深度。我們一直在研究一個集合內部的“父子”、“兄弟”關係。

然而，在現實世界中，我們還經常遇到另一類完全不同的問題，它不關心“層級”，只關心“分組”與“歸屬”。

想象一下：

最初：我們有成千上萬個居民，每個人都是一個獨立的個體（n 個元素，n 個獨立的集合）。
操作1：村長宣佈，張三家和李四家“聯誼”了，從此併為一個大家族（合併 Union：將兩個集合合併）。
操作2：你需要快速判斷，王五和趙六是不是“自家人”？（查找 Find：查詢兩個元素是否在同一個集合中）。

這種專門用來處理“動態集合合併”與“歸屬關係查詢”問題的利器，就是我們下一篇文章將要探索的，看似簡單卻藴含驚人效率的數據結構：並查集 。

本文章為轉載內容，我們尊重原作者對文章享有的著作權。如有內容錯誤或侵權問題，歡迎原作者聯繫我們進行內容更正或刪除文章。

雲端創新者博客

雲端創新者博客

博客 / 詳情