1、二維插值之插值節點為網格節點
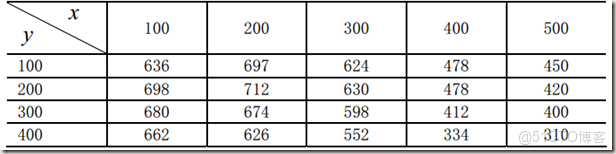
已知m x n個節點:(xi,yj,zij)(i=1…m,j=1…n),且xi,yi遞增。求(x,y)處的插值z。
Matlab可以直接調用interp2(x0,y0,z0,x,y,`method`)
m 維和 n 維向量,表示節點, z0 為 n × m 維矩陣,表示節點值, x,y
為一維數組,表示插值點, x 與 y 應是方向不同的向量,即一個是行向量,另一個是列
向量, z 為矩陣,它的行數為 y 的維數,列數為 x 的維數,表示得到的插值, 'method'
的用法同上面的一維插值。
如果是三次樣條插值,可以使用命令
pp=csape({x0,y0},z0,conds,valconds), z=fnval(pp,{x,y})其中 x0,y0 分別為 m 維和 n 維向量, z0 為 m × n 維矩陣, z 為矩陣,它的行數為 x 的維
數,列數為 y 的維數,表示得到的插值,具體使用方法同一維插值。
eg:
(1)、用interp2函數插值:
x=100:100:500;
y=100:100:400;
z=[636 697 624 478 450
698 712 630 478 420
680 674 598 412 400
662 626 552 334 310];
p=100:1:500;
q=100:1:400;
q=q';%須為列向量
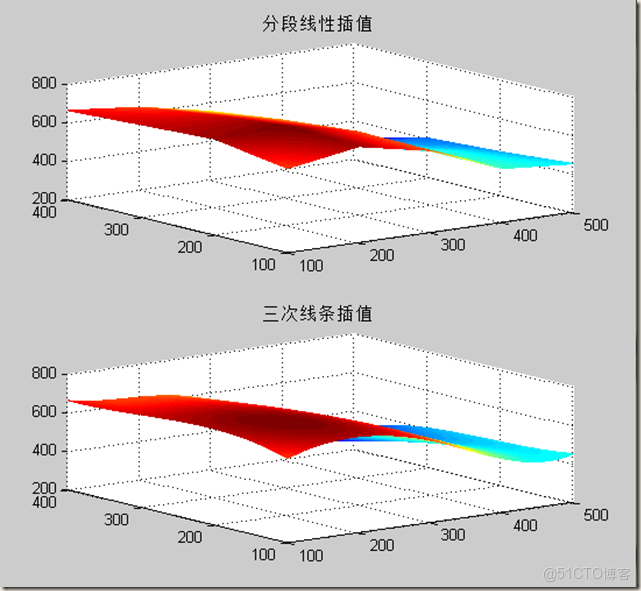
z0=interp2(x,y,z,p,q);%分段線性插值
z1=interp2(x,y,z,p,q,'spline');%三次線條插值
subplot(2,1,1);
mesh(p,q,z0);
title('分段線性插值');
subplot(2,1,2);
mesh(p,q,z1);
title('三次線條插值');
%可以觀察出,三次線條插值的圖像更平滑運行結果:
(2)、用csape函數插值:
x=100:100:500;
y=100:100:400;
z=[636 697 624 478 450
698 712 630 478 420
680 674 598 412 400
662 626 552 334 310];
p=100:1:500;
q=100:1:400;
q=q';
%三次線條插值
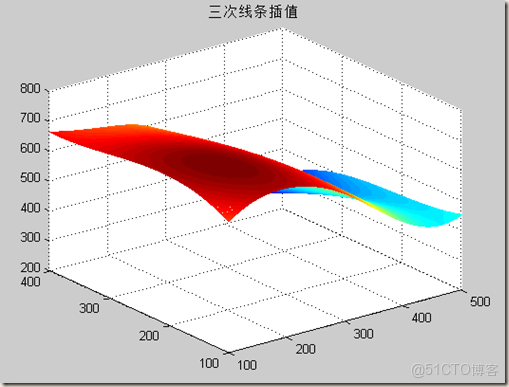
pp=csape({x,y},z');%注意跟interp2的區別,有個轉置
z0=fnval(pp,{p,q});
mesh(p,q,z0');%注意跟interp2的區別,有個轉置
title('三次線條插值');運行結果:
2、二維插值之插值節點為散亂節點
已知 n 個節點: ( xi , yi , zi )(i = 1,2,…, n) ,求點 (x, y) 處的插值 z 。
對上述問題, Matlab 中提供了插值函數 griddata,其格式為:
ZI = GRIDDATA(X,Y,Z,XI,YI)
其中 X、 Y、 Z 均為 n 維向量,指明所給數據點的橫座標、縱座標和豎座標。向量 XI、
YI 是給定的網格點的橫座標和縱座標,返回值 ZI 為網格( XI, YI)處的函數值。 XI
與 YI 應是方向不同的向量,即一個是行向量,另一個是列向量。
eg:
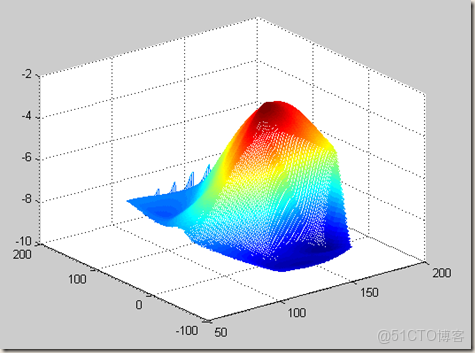
%散亂節點的二維插值
x=[129 140 103.5 88 185.5 195 105 157.5 107.5 77 81 162 162 117.5];
y=[7.5 141.5 23 147 22.5 137.5 85.5 -6.5 -81 3 56.5 -66.5 84 -33.5];
z=-[4 8 6 8 6 8 8 9 9 8 8 9 4 9];
x0=[75:1:200];
y0=[-85:1:145]';
z0=griddata(x,y,z,x0,y0,'cubic');%保凹凸性3次插值
%[xx,yy]=meshgrid(x0,y0);無需採樣,故不需要該函數
mesh(x0,y0,z0);運行結果:
在上述問題中,補上尋找最大值的程序:
%max(z0)返回一個行向量,向量的第i個元素是矩陣A的第i列上的最大值
%find(A) 尋找矩陣A非零元素下標,返回矩陣A中非零元素所在位置
%[i,j,v]=find(A)返回矩陣A中非零元素所在的行i,列j,和元素的值v(按所在位置先後順序輸出)
[p,q]=find(z0==max(max(z0)));
zmax=z0(p,q)3、最小二乘法實現曲線擬合
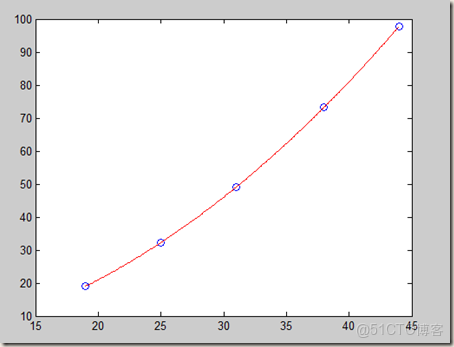
(1)用最小二乘法求一個形如 y = a + bx^ 2 的經驗公式:
%等價於[1,x^2][a;b]=y,轉換成解超定方程問題,超定方程的解是根據最小二乘法得來的
x=[19 25 31 38 44]';
y=[19.0 32.3 49.0 73.3 97.8]';
r=[ones(5,1),x.^2]
ab=r\y
x0=19:0.1:44;
y0=ab(1)+ab(2)*x0.^2;
plot(x,y,'o',x0,y0,'r')(2)多項式擬合
%a=polyfit(x,y,n)用多項式求過已知點的表達式,其中x為源數據點對應的橫座標,可為行向量、矩陣,y為源數據點對應的縱座標,可為行向量、矩陣,n為你要擬合的階數,一階直線擬合,二階拋物線擬合,並非階次越高越好,看擬合情況而定,a為m+1的行向量。polyfit函數的數學基礎是最小二乘法曲線擬合原理,所得到的函數值在基點處的值與原來點的座標偏差最小,常用於數據擬合,polyfit 做出來的值從左到右表示從高次到低次的多項式係數。
如果要求擬合函數在x`點的函數值,可以調用polyval(a,x`)函數
eg:
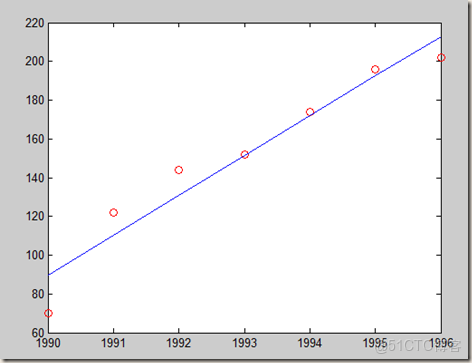
x0=[1990 1991 1992 1993 1994 1995 1996];
y0=[70 122 144 152 174 196 202];
%畫出散點圖
plot(x0,y0,'ro');
hold on
%用線性擬合
p=polyfit(x0,y0,1);
z0=polyval(p,x0);
plot(x0,z0);運行結果:
4、最小二乘優化 (最小二乘:least square)
1、lsqlin函數
eg:
%擬合形如y=a+bx^2的函數
%採樣點
x=[19 25 31 38 44]';
y=[19 32.3 49 73.3 97.8]';
r=[ones(5,1),x.^2];
ab=lsqlin(r,y)
x0=19:0.1:44;
y0=ab(1)+ab(2)*x0.^2;
plot(x,y,'o',x0,y0,'r')運行結果:
5、曲線擬合與函數逼近
eg:
求 f(x) =cos x, (-pi/2<=x<=pi/2) 在 H = Span{1, x^2 , x^4} 中的最佳平方逼近多項式。
程序如下:
syms x%定義符號數值
base=[1,x^2,x^4];
y1=base.'*base
y2=cos(x)*base.'
r1=int(y1,-pi/2,pi/2)
r2=int(y2,-pi/2,pi/2)
a=r1\r2%a為符號數值
xishu1=double(a)%化簡符號數值
digits(8)%設置符號數值的精度
xishu2=vpa(a)%任意精度(符號類)數值運行結果:
|
所以y的最佳平方逼近多項式為y=0.9996-0.4964x^2+0.0372x^4