LSTM與圖卷積網絡結合的社交網絡行為預測。
GCN像朋友圈加權平均器,把每個人在當前時刻的狀態,和TA朋友圈(圖的鄰居)的狀態融合起來,得到一個考慮社會影響的時刻表徵。
LSTM像記憶管家,把過去一段時間(多個時刻)的融合表徵傳進記憶單元,學最近是火了還是冷了,有沒有周期性等時間規律。
合體後,相當於先看社交圈,再看時間史,預測下一刻的行為,是不是很酷!~
底層原理
給定一個社交網絡圖,其中是用户/節點數,是邊(好友關係、關注關係等)。
設為鄰接矩陣(可以是無向或有向,這裏先當無向,元素為0/1或權重)。
在時間,每個節點有特徵向量(如過去一小時發帖數、點贊數、話題向量等)。把所有節點堆起來記為。
目標是預測下一時刻每個節點的某個行為(比如二分類:是否會點贊/轉發;或迴歸:互動量)。
這裏我們以二分類為例,。
圖卷積(GCN)層
常用的對稱歸一化(帶自環):
一層GCN將投到隱藏維度:
其中, 為可學習參數,為非線性(如ReLU)。直觀理解:先把每個節點和其鄰居(含自己)的特徵做歸一化加權平均,再線性變換並過非線性。
時間序列與LSTM
對每個時間,先用GCN對做圖卷積,得到圖結構融合後的表徵:
是GCN輸出維度。
對每個節點,我們收集一個長度為的時間窗口:
把這個序列輸入LSTM,得到最後時刻的隱藏狀態(或用全部時刻的隱藏狀態再聚合):
最終分類頭(全連接+sigmoid)預測下一時刻的行為概率:
LSTM內部門門
LSTM有輸入門、遺忘門、輸出門控制記憶單元與隱藏狀態,標準公式為:
這裏就是該節點在時刻的圖表徵。
損失函數與訓練
二分類用二元交叉熵(帶Logits更穩):
評估指標常用AUC、F1、Accuracy等。
融合方式小對比
先GCN後LSTM(本例):每個時刻圖卷積得到,餵給LSTM。這是最直觀、工程裏常見的。
先LSTM後GCN:先沿時間對每個節點做LSTM編碼,再在最後時刻做一次GCN聚合。適合最後時刻前的個人時間軌跡很重要的場景。
時空圖方法(進階):如DCRNN、ST-GCN、TGAT、T-GCN等,把圖結構和時間卷積/注意力更緊耦合,但實現複雜度更高。
完整實戰案例
我們在代碼中,會造一個具有社區結構的社交圖(隨機分塊模型),生成帶時間依賴與鄰居影響的節點特徵,並用它們生成下一時刻的二分類label(是否活躍/互動)。
模型:每個時間步先用GCN做圖聚合,形成時序嵌入,再餵給LSTM預測下一刻行為。
我們還給出兩個簡單對照:LSTM-only(不看圖),GCN-only(不看時間,僅用最後時刻)對比AUC。import os
import random
import math
import time
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import networkx as nx
from sklearn.metrics import roc_auc_score, accuracy_score
from sklearn.preprocessing import StandardScaler
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import Dataset, DataLoader
# 0. 基礎設置
def set_seed(seed=42):
random.seed(seed)
np.random.seed(seed)
torch.manual_seed(seed)
set_seed(42)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# 1. 生成帶社區結構的圖
N = 60 # 節點數
num_communities = 3
sizes = [N // num_communities] * num_communities
p_intra = 0.15 # 社區內連邊概率
p_inter = 0.02 # 社區間連邊概率
# 概率塊矩陣
probs = [[p_intra if i==j else p_inter for j in range(num_communities)] for i in range(num_communities)]
G = nx.stochastic_block_model(sizes, probs, seed=42)
# 確保無自環(後面會手動加自環)
G.remove_edges_from(nx.selfloop_edges(G))
A = nx.to_numpy_array(G) # 鄰接矩陣
# 加自環
A_hat = A + np.eye(N)
# 對稱歸一化
D_hat = np.diag(1.0 / np.sqrt(A_hat.sum(axis=1) + 1e-8))
A_norm = D_hat @ A_hat @ D_hat # \tilde{A}
# 社區標籤
community_labels = []
for c_idx, size in enumerate(sizes):
community_labels += [c_idx]*size
community_labels = np.array(community_labels)
# 2. 生成時間序列特徵與標籤
T_total = 220 # 總時刻
F_in = 4 # 節點特徵維度
X = np.zeros((T_total, N, F_in), dtype=np.float32)
Y = np.zeros((T_total, N), dtype=np.float32) # y_t: 表示時刻t的行為(我們預測y_{t+1})
# 初始特徵
X[0] = np.random.randn(N, F_in).astype(np.float32)
# 社區偏置(節點的內在活躍偏好)
community_bias = np.array([0.5, 0.0, -0.2]) # 3個社區
node_bias = np.array([community_bias[c] for c in community_labels]) + np.random.randn(N)*0.1
# 構造時間依賴 + 鄰居影響 + 季節項
w = np.array([1.0, -0.5, 0.8, 0.3]) # 特徵到活躍傾向的權重
alpha_neighbor = 0.6 # 鄰居平均影響
noise_scale = 0.1
# 生成動態特徵 X_{t+1} = 0.6 X_t + 0.3 A_norm X_t + noise + 季節項
for t in range(T_total - 1):
seasonal = np.sin(2 * np.pi * t / 24.0) * 0.1 # 日週期
neighbor_info = A_norm @ X[t] # [N, F]
X[t+1] = 0.6*X[t] + 0.3*neighbor_info + noise_scale*np.random.randn(N, F_in)
X[t+1][:, 0] += seasonal # 給第一個特徵加入季節項
# 標籤生成:y_t基於X_t、鄰居均值、節點偏置、季節項
def sigmoid(x):
return 1.0 / (1.0 + np.exp(-x))
for t in range(T_total):
neigh_mean = (A_norm @ X[t]) # [N, F]
seasonal = np.sin(2 * np.pi * t / 24.0) * 0.1
logits = (X[t] @ w) + alpha_neighbor * (neigh_mean @ w) + node_bias + seasonal
prob = sigmoid(logits)
Y[t] = (np.random.rand(N) < prob).astype(np.float32)
# 我們預測 y_{t+1},因此有效樣本時間為 t=L-1 .. T_total-2
# 3. 時間切分與避免泄露
# 時間切分(按時間連續分段)
train_ratio, val_ratio = 0.6, 0.2
train_end = int(T_total * train_ratio) # 訓練段最後時刻索引(包含)
val_end = int(T_total * (train_ratio + val_ratio)) # 驗證段最後時刻索引(包含)
# 注意預測是 y_{t+1},所以窗口結束時刻 t 的 target 是 t+1
L = 8 # 時間窗口長度
# 標準化:只用訓練段的特徵統計量(避免泄露)
scaler = StandardScaler()
# 訓練段可用於窗口輸入的時刻範圍:0..train_end-1
train_feature_times = list(range(0, train_end))
X_train_flat = X[train_feature_times].reshape(-1, F_in)
scaler.fit(X_train_flat)
X_scaled = X.copy()
X_scaled = X_scaled.reshape(-1, F_in)
X_scaled = scaler.transform(X_scaled).reshape(T_total, N, F_in).astype(np.float32)
# 4. 構建窗口數據集
class WindowDataset(Dataset):
def __init__(self, X_scaled, Y, split="train", L=8, train_end=132, val_end=176):
super().__init__()
self.X = X_scaled # [T, N, F]
self.Y = Y # [T, N]
self.L = L
self.split = split
self.T_total = X_scaled.shape[0]
# 根據split決定可用的目標時間範圍(target時刻t+1屬於該split)
if split == "train":
# target時刻在 1..train_end,且窗口結束時刻t滿足 t+1 <= train_end
self.t_start = L - 1
self.t_end = train_end - 1 # t的上限,保證t+1<=train_end
elif split == "val":
# target時刻在 train_end+1 .. val_end
self.t_start = max(L - 1, train_end) # 窗口結束時刻t>=train_end,target=t+1在 val段
self.t_end = val_end - 1
elif split == "test":
# target時刻在 val_end+1 .. T_total-1
self.t_start = max(L - 1, val_end)
self.t_end = self.T_total - 2 # 因為t+1<=T_total-1
else:
raise ValueError("split must be train/val/test")
self.idxs = list(range(self.t_start, self.t_end + 1))
def __len__(self):
return len(self.idxs)
def __getitem__(self, idx):
t = self.idxs[idx] # 窗口結束時刻
x_window = self.X[t - self.L + 1: t + 1] # [L, N, F]
y_target = self.Y[t + 1] # [N]
return torch.from_numpy(x_window), torch.from_numpy(y_target)
train_dataset = WindowDataset(X_scaled, Y, split="train", L=L, train_end=train_end, val_end=val_end)
val_dataset = WindowDataset(X_scaled, Y, split="val", L=L, train_end=train_end, val_end=val_end)
test_dataset = WindowDataset(X_scaled, Y, split="test", L=L, train_end=train_end, val_end=val_end)
train_loader = DataLoader(train_dataset, batch_size=16, shuffle=True, drop_last=False)
val_loader = DataLoader(val_dataset, batch_size=32, shuffle=False, drop_last=False)
test_loader = DataLoader(test_dataset, batch_size=32, shuffle=False, drop_last=False)
# 5. 定義GCN層與混合模型(GCN + LSTM)
A_norm_torch = torch.from_numpy(A_norm).float().to(device)
class GraphConvolution(nn.Module):
def __init__(self, in_feats, out_feats, bias=True):
super().__init__()
self.lin = nn.Linear(in_feats, out_feats, bias=bias)
def forward(self, X): # X: [B, N, F]
# 先做鄰居聚合: \tilde{A} X
AX = torch.einsum('ij,bjf->bif', A_norm_torch, X) # [B, N, F]
return self.lin(AX) # [B, N, out_feats]
class GCN_LSTM_Model(nn.Module):
def __init__(self, in_feats=F_in, gcn_hidden=32, gcn_out=32, lstm_hidden=64, num_layers=1, dropout=0.3):
super().__init__()
self.gcn1 = GraphConvolution(in_feats, gcn_hidden)
self.gcn2 = GraphConvolution(gcn_hidden, gcn_out)
self.act = nn.ReLU()
self.dropout = nn.Dropout(dropout)
self.lstm = nn.LSTM(input_size=gcn_out, hidden_size=lstm_hidden, num_layers=num_layers, batch_first=True)
self.fc = nn.Linear(lstm_hidden, 1) # 每個節點一個logit
def forward(self, x_seq): # x_seq: [B, L, N, F]
B, L_, N_, F_ = x_seq.shape
# 逐時間步做GCN(共享權重)
gcn_embs = []
for t in range(L_):
x_t = x_seq[:, t, :, :] # [B, N, F]
h = self.gcn1(x_t)
h = self.act(h)
h = self.dropout(h)
h = self.gcn2(h)
h = self.act(h)
h = self.dropout(h) # [B, N, gcn_out]
gcn_embs.append(h)
gcn_embs = torch.stack(gcn_embs, dim=1) # [B, L, N, gcn_out]
# 對每個節點獨立地餵給LSTM:重排維度 [B*N, L, gcn_out]
BN = B * N_
gcn_embs_reshaped = gcn_embs.permute(0, 2, 1, 3).contiguous().view(BN, L_, -1)
lstm_out, (h_n, c_n) = self.lstm(gcn_embs_reshaped) # h_n: [num_layers, BN, lstm_hidden]
last_hidden = h_n[-1] # [BN, lstm_hidden]
logits = self.fc(last_hidden).view(B, N_) # [B, N]
return logits
# 6. 定義兩個對照模型(消融)
class LSTM_Only_Model(nn.Module):
def __init__(self, in_feats=F_in, lstm_hidden=64, num_layers=1, dropout=0.3):
super().__init__()
self.lstm = nn.LSTM(input_size=in_feats, hidden_size=lstm_hidden, num_layers=num_layers, batch_first=True)
self.dropout = nn.Dropout(dropout)
self.fc = nn.Linear(lstm_hidden, 1)
def forward(self, x_seq): # x_seq: [B, L, N, F]
B, L_, N_, F_ = x_seq.shape
# [B, N, L, F] -> [B*N, L, F]
x_reshaped = x_seq.permute(0, 2, 1, 3).contiguous().view(B*N_, L_, F_)
out, (h_n, c_n) = self.lstm(x_reshaped)
last_hidden = self.dropout(h_n[-1]) # [B*N, H]
logits = self.fc(last_hidden).view(B, N_)
return logits
class GCN_Only_Model(nn.Module):
# 非時序:只用最後一步的X_t做GCN,再線性分類 y_{t+1}
def __init__(self, in_feats=F_in, gcn_hidden=32, gcn_out=32, dropout=0.3):
super().__init__()
self.gcn1 = GraphConvolution(in_feats, gcn_hidden)
self.gcn2 = GraphConvolution(gcn_hidden, gcn_out)
self.act = nn.ReLU()
self.dropout = nn.Dropout(dropout)
self.fc = nn.Linear(gcn_out, 1)
def forward(self, x_seq): # x_seq: [B, L, N, F], 只取最後時刻
x_t = x_seq[:, -1, :, :] # [B, N, F]
h = self.gcn1(x_t); h = self.act(h); h = self.dropout(h)
h = self.gcn2(h); h = self.act(h); h = self.dropout(h)
logits = self.fc(h).squeeze(-1) # [B, N]
return logits
# 7. 訓練與評估函數
def train_one_epoch(model, loader, optimizer, criterion):
model.train()
total_loss = 0.0
y_true_all, y_prob_all = [], []
for x_win, y_tgt in loader:
x_win = x_win.to(device) # [B,L,N,F]
y_tgt = y_tgt.to(device) # [B,N]
optimizer.zero_grad()
logits = model(x_win) # [B,N]
loss = criterion(logits, y_tgt)
loss.backward()
optimizer.step()
total_loss += loss.item() * x_win.size(0)
with torch.no_grad():
prob = torch.sigmoid(logits).detach().cpu().numpy().ravel()
y_true_all.append(y_tgt.detach().cpu().numpy().ravel())
y_prob_all.append(prob)
y_true_all = np.concatenate(y_true_all)
y_prob_all = np.concatenate(y_prob_all)
try:
auc = roc_auc_score(y_true_all, y_prob_all)
except:
auc = np.nan
return total_loss / len(loader.dataset), auc
@torch.no_grad()
def evaluate(model, loader, criterion):
model.eval()
total_loss = 0.0
y_true_all, y_prob_all = [], []
for x_win, y_tgt in loader:
x_win = x_win.to(device)
y_tgt = y_tgt.to(device)
logits = model(x_win)
loss = criterion(logits, y_tgt)
total_loss += loss.item() * x_win.size(0)
prob = torch.sigmoid(logits).cpu().numpy().ravel()
y_true_all.append(y_tgt.cpu().numpy().ravel())
y_prob_all.append(prob)
y_true_all = np.concatenate(y_true_all)
y_prob_all = np.concatenate(y_prob_all)
try:
auc = roc_auc_score(y_true_all, y_prob_all)
except:
auc = np.nan
return total_loss / len(loader.dataset), auc
# BCE with logits
class BCEWithLogitsNodeWise(nn.Module):
def __init__(self):
super().__init__()
self.bce = nn.BCEWithLogitsLoss(reduction='mean')
def forward(self, logits, targets):
return self.bce(logits, targets)
# 8. 訓練主模型(GCN+LSTM)
gcn_lstm = GCN_LSTM_Model(in_feats=F_in, gcn_hidden=32, gcn_out=32, lstm_hidden=64, num_layers=1, dropout=0.3).to(device)
criterion = BCEWithLogitsNodeWise()
optimizer = optim.Adam(gcn_lstm.parameters(), lr=1e-3, weight_decay=1e-4)
best_val_auc = -1
best_state = None
num_epochs = 25
history = {"train_loss": [], "train_auc": [], "val_loss": [], "val_auc": []}
for epoch in range(1, num_epochs+1):
tr_loss, tr_auc = train_one_epoch(gcn_lstm, train_loader, optimizer, criterion)
val_loss, val_auc = evaluate(gcn_lstm, val_loader, criterion)
history["train_loss"].append(tr_loss)
history["train_auc"].append(tr_auc)
history["val_loss"].append(val_loss)
history["val_auc"].append(val_auc)
print(f"[GCN+LSTM][Epoch {epoch:02d}] train_loss={tr_loss:.4f} train_auc={tr_auc:.4f} val_loss={val_loss:.4f} val_auc={val_auc:.4f}")
if val_auc > best_val_auc:
best_val_auc = val_auc
best_state = gcn_lstm.state_dict()
# 加載最佳驗證AUC的權重
if best_state is not None:
gcn_lstm.load_state_dict(best_state)
test_loss, test_auc = evaluate(gcn_lstm, test_loader, criterion)
print(f"[GCN+LSTM] TEST: loss={test_loss:.4f} auc={test_auc:.4f}")
# 9. 訓練對照模型
def train_and_eval_model(model, name, epochs=20):
model = model.to(device)
optimizer = optim.Adam(model.parameters(), lr=1e-3, weight_decay=1e-4)
best_val_auc = -1
best_state = None
for ep in range(1, epochs+1):
tr_loss, tr_auc = train_one_epoch(model, train_loader, optimizer, criterion)
val_loss, val_auc = evaluate(model, val_loader, criterion)
# print(f"[{name}][Epoch {ep:02d}] train_loss={tr_loss:.4f} train_auc={tr_auc:.4f} val_auc={val_auc:.4f}")
if val_auc > best_val_auc:
best_val_auc = val_auc
best_state = model.state_dict()
if best_state is not None:
model.load_state_dict(best_state)
test_loss, test_auc = evaluate(model, test_loader, criterion)
print(f"[{name}] TEST: loss={test_loss:.4f} auc={test_auc:.4f}")
return test_auc, model
lstm_only = LSTM_Only_Model(in_feats=F_in, lstm_hidden=64, num_layers=1, dropout=0.3)
gcn_only = GCN_Only_Model(in_feats=F_in, gcn_hidden=32, gcn_out=32, dropout=0.3)
auc_lstm_only, lstm_only = train_and_eval_model(lstm_only, "LSTM-only", epochs=20)
auc_gcn_only, gcn_only = train_and_eval_model(gcn_only, "GCN-only", epochs=20)
# 10. 可視化分析
# 圖1:社交圖可視化(社區着色)
plt.figure(figsize=(8,6))
pos = nx.spring_layout(G, seed=42)
colors = np.array(['#ff595e', '#1982c4', '#8ac926'])
node_colors = [colors[c] for c in community_labels]
node_sizes = (A.sum(axis=1) + 3) * 25 # 稍微按度加權
nx.draw_networkx_nodes(G, pos, node_color=node_colors, node_size=node_sizes, alpha=0.9)
nx.draw_networkx_edges(G, pos, alpha=0.3, edge_color="#6a4c93")
plt.title("社交網絡圖(社區着色)", color="#333333")
plt.axis('off')
plt.tight_layout()
plt.show()
# 圖2:訓練曲線(訓練Loss & 驗證AUC)
fig, ax1 = plt.subplots(figsize=(9,5))
epochs = np.arange(1, num_epochs+1)
color1 = sns.color_palette("plasma", 10)[2]
color2 = sns.color_palette("viridis", 10)[8]
ax1.plot(epochs, history["train_loss"], color=color1, lw=2.5, label="Train Loss")
ax1.set_xlabel("Epoch")
ax1.set_ylabel("Loss", color=color1)
ax1.tick_params(axis='y', labelcolor=color1)
ax2 = ax1.twinx()
ax2.plot(epochs, history["val_auc"], color=color2, lw=2.5, label="Val AUC")
ax2.set_ylabel("AUC", color=color2)
ax2.tick_params(axis='y', labelcolor=color2)
plt.title("訓練過程:損失與驗證AUC", color="#333333")
fig.tight_layout()
plt.show()
# 圖3:測試期**真實均值 vs 預測均值**的時間序列
# 為了繪製,逐步滑動窗口,在測試段生成預測,並與真實y_{t+1}對比(均值)
@torch.no_grad()
def rolling_predict_mean(model, X_scaled, start_idx, end_idx, L):
# 對於每個窗口結束時刻t(start_idx .. end_idx-1),預測 y_{t+1}
preds_mean = []
trues_mean = []
times = []
for t in range(start_idx, end_idx):
x_win = X_scaled[t-L+1:t+1] # [L,N,F]
x_win_t = torch.from_numpy(x_win).unsqueeze(0).to(device) # [1,L,N,F]
logits = model(x_win_t) # [1,N]
prob = torch.sigmoid(logits).cpu().numpy()[0] # [N]
y_true = Y[t+1] # [N]
preds_mean.append(prob.mean())
trues_mean.append(y_true.mean())
times.append(t+1)
return np.array(times), np.array(trues_mean), np.array(preds_mean)
test_start = test_dataset.t_start
test_end_ = test_dataset.t_end
times, true_mean, pred_mean = rolling_predict_mean(gcn_lstm, X_scaled, test_start, test_end_, L)
plt.figure(figsize=(10,5))
plt.plot(times, true_mean, color="#ff0054", lw=2.5, label="真實活躍均值")
plt.plot(times, pred_mean, color="#3a86ff", lw=2.5, label="預測活躍均值")
plt.fill_between(times, true_mean, pred_mean, color="#ffbe0b", alpha=0.2)
plt.xlabel("時間")
plt.ylabel("活躍比例")
plt.title("測試期:真實 vs 預測(全網平均)", color="#333333")
plt.legend()
plt.tight_layout()
plt.show()
# 圖4:消融對比(AUC柱狀圖)
labels = ["GCN+LSTM", "LSTM-only", "GCN-only"]
auc_vals = [test_auc, auc_lstm_only, auc_gcn_only]
palette = ["#ff595e", "#3a86ff", "#8ac926"]
plt.figure(figsize=(7,5))
bars = plt.bar(labels, auc_vals, color=palette, alpha=0.85)
for b, v in zip(bars, auc_vals):
plt.text(b.get_x() + b.get_width()/2.0, v+0.005, f"{v:.3f}", ha="center", color="#333333", fontsize=12)
plt.ylim(0.5, 1.0)
plt.ylabel("AUC")
plt.title("消融對比:測試AUC", color="#333333")
plt.tight_layout()
plt.show()
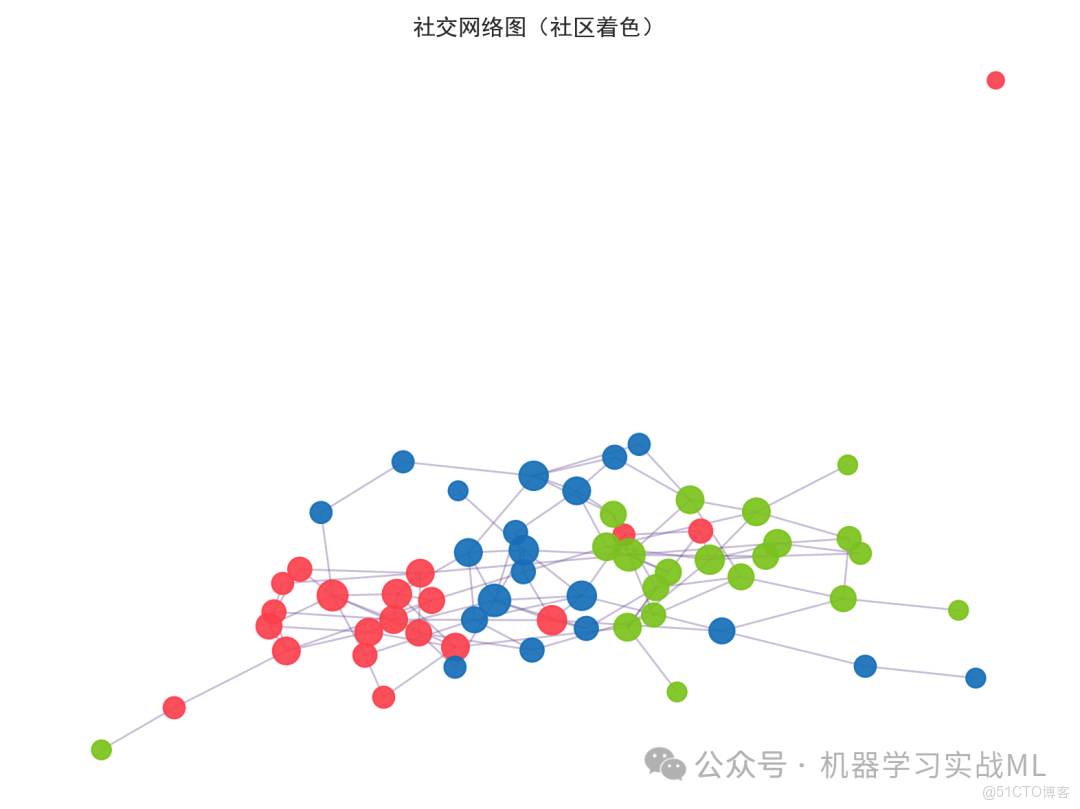
社交網絡圖(社區着色):
用spring_layout畫出60個節點的圖,節點顏色按3個社區着色(紅/藍/綠),連邊半透明,節點大小與度數正相關。
展示網絡的社區結構與連通關係。真實社交網絡裏,社區有相似興趣/話題,會彼此更強影響。GCN正是利用這些鄰接關係,把鄰居的信息融合進來。
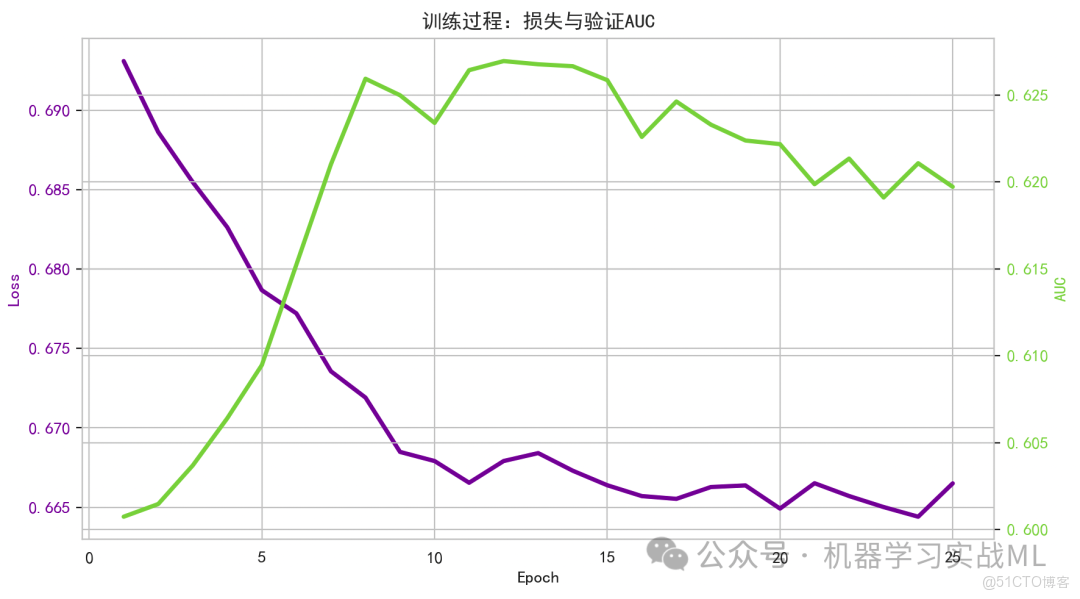
訓練曲線(訓練Loss & 驗證AUC):
在同一張圖上用雙y軸畫訓練Loss(plasma配色)和驗證AUC(viridis配色),隨epoch變化的趨勢。
Loss下降、驗證AUC上升通常意味着模型學習到有效規律。若驗證AUC掉頭下滑,可能過擬合,需要正則化或早停。本例我們用驗證AUC選擇最佳權重。
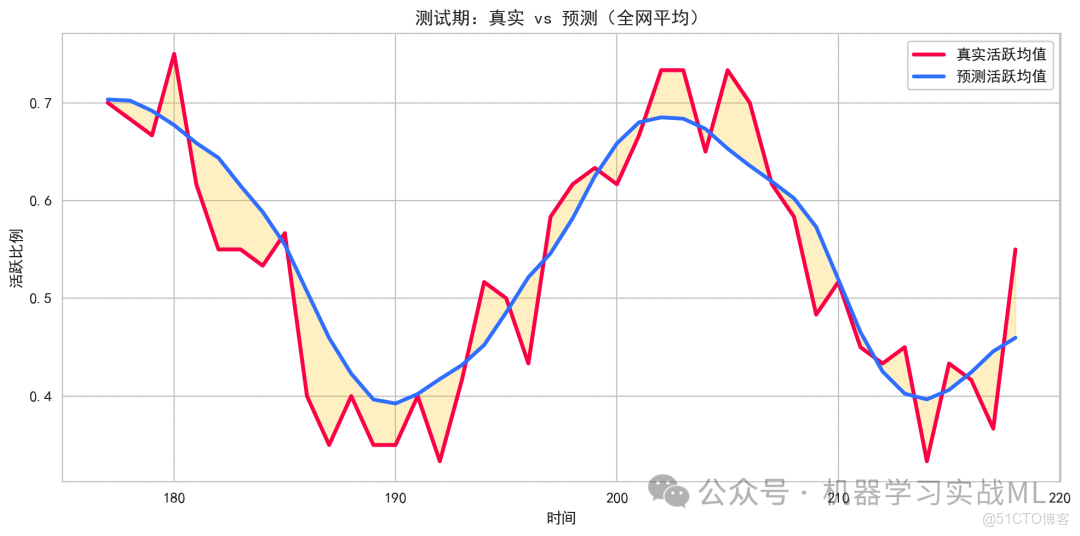
測試期真實均值 vs 預測均值的時間序列:
對測試時間段逐時滑動,用模型預測下一刻全網平均活躍概率(取所有節點概率的均值),對比真實活躍比例(所有節點標籤的均值)。
看模型能否跟上整體活躍度的起伏,比如週期性波動。兩條曲線較為貼近,且隨季節項/週期項(我們合成數據裏有sin波)變化一致,説明模型捕捉了宏觀動態。
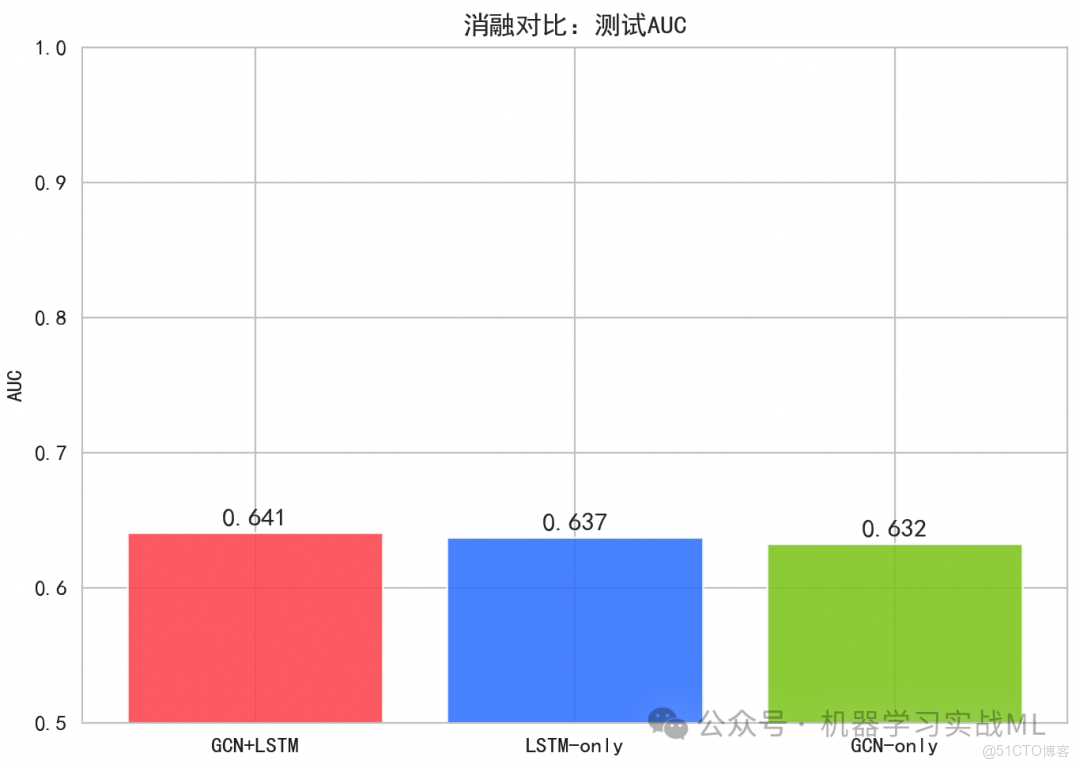
消融對比(AUC柱狀圖):
比較GCN+LSTM、LSTM-only、GCN-only的測試AUC。
通常GCN+LSTM應優於單獨LSTM或單獨GCN,説明同時利用圖結構依賴和時間依賴更有優勢。在我們的合成數據中,鄰居影響和時間趨勢都是真實存在的,因此融合模型效果更好。
總的來説,社交網絡行為預測的核心是誰影響了誰(圖結構)和什麼時候發生了什麼(時間序列);GCN負責鄰居信息融合,LSTM負責時間依賴建模。
正確的時間切分和特徵標準化是防止泄露的關鍵。
在合成數據的實驗中,融合模型GCN+LSTM在測試集AUC上優於僅LSTM或僅GCN,驗證了結構+時序聯合建模的優勢。
大家可以把這套代碼作為你自己的數據的起點模板,按照同樣的切分與訓練規約替換數據即可,但是一定要注意,務必保持嚴格的時間因果順序。