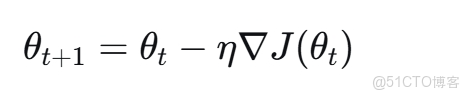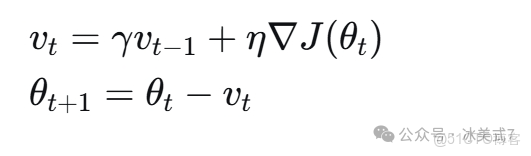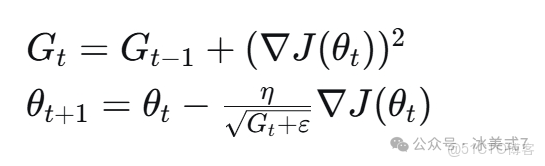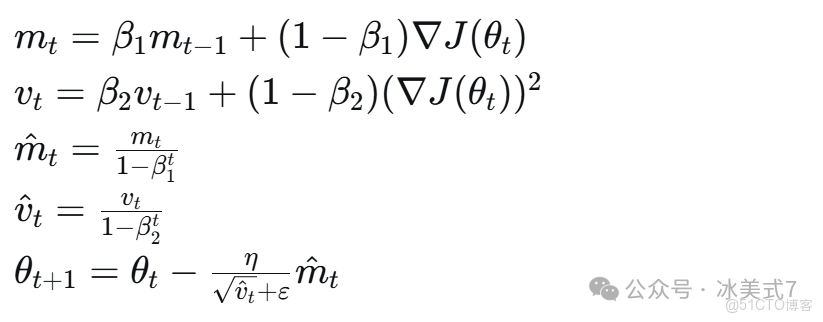在深度學習領域,卷積神經網絡(CNN)已成為圖像識別任務的首選架構。而在CNN訓練過程中,優化器的選擇對模型性能有着至關重要的影響。本文將深入探討多種優化算法的原理,並通過手寫數字識別任務對比它們的實際表現。
優化器原理詳解
1. 隨機梯度下降(SGD)
隨機梯度下降是最基礎的優化算法,其更新公式為:
其中$η$是學習率,$∇J(θ_t)$是損失函數在$θ_t$處的梯度。
SGD的優點是簡單易懂,計算開銷小,但缺點是容易陷入局部最優,收斂速度慢,且對學習率的選擇非常敏感。
2. Momentum(動量優化)
Momentum算法在SGD基礎上引入了動量項,模擬物理中的動量概念:
其中$γ$是動量係數(通常設為0.9),$v_t$是當前的速度向量。
Momentum的優點:
- 加速收斂過程
- 減少參數更新的震盪
- 有助於跳出局部最小值
3. Adagrad(自適應梯度)
Adagrad算法為每個參數自適應地調整學習率:
其中$G_t$是梯度平方的累積和,$ε$是為數值穩定性添加的小常數。
Adagrad的優點:
- 自動調整每個參數的學習率
- 適合處理稀疏數據
缺點:
- 學習率會持續減小,可能導致過早停止學習
4. RMSprop(均方根傳播)
RMSprop改進了Adagrad的學習率持續下降問題:
其中$β$是衰減率(通常設為0.9),$E[g^2]_t$是梯度平方的指數移動平均。
RMSprop的優點:
- 解決了Adagrad學習率持續下降的問題
- 在非平穩目標函數上表現良好
5. Adam(自適應矩估計)
Adam結合了Momentum和RMSprop的優點:
其中$β_1$和$β_2$是衰減率(通常設為0.9和0.999),$m_t$和$v_t$分別是梯度的一階矩和二階矩估計。
Adam的優點:
- 結合了動量法和自適應學習率的優勢
- 對超參數的選擇相對魯棒
- 在實踐中表現優異
使用MNIST手寫數字數據集,構建一個包含三個卷積層和兩個全連接層的CNN模型,對比上述優化器的性能。
import tensorflow as tf
from tensorflow import keras
import numpy as np
import matplotlib.pyplot as plt
import timeclass CNN(object):
def __init__(self):
model = keras.models.Sequential()
# 第1層卷積,卷積核大小為3x3,32個,28x28為待訓練圖片的大小
model.add(keras.layers.Conv2D(
filters=32,
kernel_size=(3,3),
activatinotallow='relu',
input_shape=(28,28,1)
))
model.add(keras.layers.MaxPooling2D((2,2)))
# 第2層卷積,卷積核大小為3x3,64個
model.add(keras.layers.Conv2D(
filters=64,
kernel_size=(3,3),
activatinotallow='relu'
))
model.add(keras.layers.MaxPooling2D((2,2)))
# 第3層卷積,卷積核大小為3x3,64個
model.add(keras.layers.Conv2D(
filters=64,
kernel_size=(3,3),
activatinotallow='relu'
))
model.add(keras.layers.Flatten()) # 展平層,將多維輸入一維化
model.add(keras.layers.Dense(64, activatinotallow='relu')) # 全連接層,64個神經元
model.add(keras.layers.Dense(10, activatinotallow='softmax')) # 輸出層
self.model = model
def get_model(self):
return keras.models.clone_model(self.model)
class TrainCNN(object):
def __init__(self, model, X, y, optimizer='adam', epochs=5, batch_size=64):
self.model = model
self.X = X
self.y = y
self.epochs = epochs
self.batch_size = batch_size
self.optimizer_name = optimizer
self.history = None
self.training_time = 0
#配置優化器
if optimizer == 'sgd':
opt = keras.optimizers.SGD(learning_rate=0.01)
elif optimizer == 'momentum':
opt = keras.optimizers.SGD(learning_rate=0.01, momentum=0.9)
elif optimizer == 'adam':
opt = keras.optimizers.Adam(learning_rate=0.001)
elif optimizer == 'rmsprop':
opt = keras.optimizers.RMSprop(learning_rate=0.001)
else:
opt = keras.optimizers.Adam(learning_rate=0.001)
self.model.compile(
optimizer=opt,
loss='sparse_categorical_crossentropy',
metrics=['accuracy']
)
#訓練模型並保存訓練歷史
start_time = time.time()
self.history = self.model.fit(
self.X,
self.y,
epochs=self.epochs,
batch_size=self.batch_size,
validation_split=0.2,
verbose=0
)
self.training_time = time.time() - start_time對比了五種優化器在MNIST數據集上的表現:
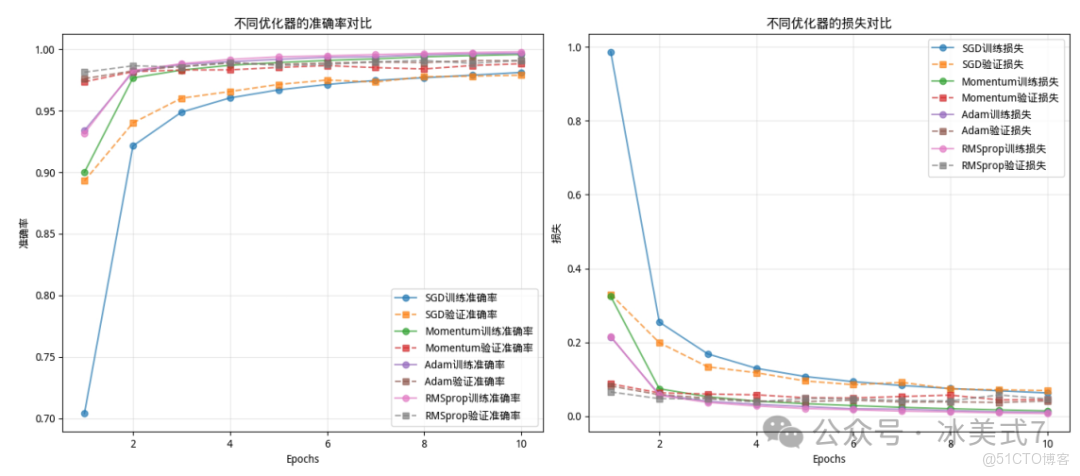
1. 收斂速度對比
從圖中看出:
a.最優表現:RMSprop和Adam在準確率和損失上均表現最佳,早期收斂快、最終準確率接近1.00、損失接近0,且訓練/驗證指標差異小,泛化能力強,適合需要快速穩定收斂的場景。
b.次優選擇:Momentum(帶動量的SGD)性能介於SGD和Adam之間,適合對收斂速度有一定要求但計算資源有限的場景。
c.最差表現:SGD(隨機梯度下降)初始效率低、收斂慢,最終損失高,僅在數據量大或需要手動調參時考慮。
整體來看,自適應學習率優化器(RMSprop、Adam)在模型訓練中綜合性能顯著優於傳統的SGD及其變種。
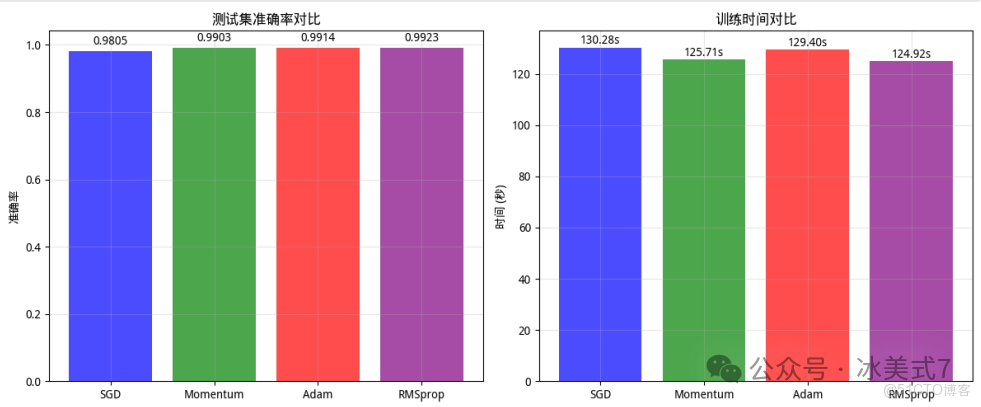
2. 測試準確率與訓練時間對比
在測試集上的表現:
左側:測試集準確率對比
SGD(藍色):準確率0.9805(最低);
Momentum(綠色):準確率0.9903;
Adam(紅色):準確率0.9914;
RMSprop(紫色):準確率0.9923(最高)。
結論:準確率從低到高排序為:SGD < Momentum < Adam < RMSprop,RMSprop準確率最優。
右側:訓練時間對比
SGD(藍色):訓練時間130.28s(最長);
Adam(紅色):訓練時間129.40s;
Momentum(綠色):訓練時間125.71s;
RMSprop(紫色):訓練時間124.92s(最短)。
結論:訓練時間從長到短排序為:SGD > Adam > Momentum > RMSprop,RMSprop訓練效率最高。
綜合對比
RMSprop在兩項指標中均表現最優:準確率最高(0.9923) 且 訓練時間最短(124.92s);SGD則準確率最低(0.9805)且訓練時間最長(130.28s)。Momentum和Adam性能居中,其中Momentum訓練時間較短(125.71s),Adam準確率略高於Momentum(0.9914 vs 0.9903)。
3.不同優化器下的部分樣本預測結果
應用場景建議:
- 簡單任務或教學演示:使用SGD,便於理解優化過程
- 標準深度學習任務:優先選擇Adam,綜合表現最佳
- 循環神經網絡:RMSprop通常表現更好
- 稀疏數據:Adagrad可能更適合
- 需要穩定訓練過程:Momentum可以減少震盪
源碼
import tensorflow as tf
from tensorflow import keras
import numpy as np
import matplotlib.pyplot as plt
import time
class CNN(object):
def __init__(self):
model = keras.models.Sequential()
# 第1層卷積,卷積核大小為3x3,32個,28x28為待訓練圖片的大小
model.add(keras.layers.Conv2D(
filters=32,
kernel_size=(3,3),
activatinotallow='relu',
input_shape=(28,28,1)
))
model.add(keras.layers.MaxPooling2D((2,2)))
# 第2層卷積,卷積核大小為3x3,64個
model.add(keras.layers.Conv2D(
filters=64,
kernel_size=(3,3),
activatinotallow='relu'
))
model.add(keras.layers.MaxPooling2D((2,2)))
# 第3層卷積,卷積核大小為3x3,64個
model.add(keras.layers.Conv2D(
filters=64,
kernel_size=(3,3),
activatinotallow='relu'
))
model.add(keras.layers.Flatten()) # 展平層,將多維輸入一維化
model.add(keras.layers.Dense(64, activatinotallow='relu')) # 全連接層,64個神經元
model.add(keras.layers.Dense(10, activatinotallow='softmax')) # 輸出層
self.model = model
def get_model(self):
return keras.models.clone_model(self.model)
class TrainCNN(object):
def __init__(self, model, X, y, optimizer='adam', epochs=5, batch_size=64):
self.model = model
self.X = X
self.y = y
self.epochs = epochs
self.batch_size = batch_size
self.optimizer_name = optimizer
self.history = None
self.training_time = 0
#配置優化器
if optimizer == 'sgd':
opt = keras.optimizers.SGD(learning_rate=0.01)
elif optimizer == 'momentum':
opt = keras.optimizers.SGD(learning_rate=0.01, momentum=0.9)
elif optimizer == 'adam':
opt = keras.optimizers.Adam(learning_rate=0.001)
elif optimizer == 'rmsprop':
opt = keras.optimizers.RMSprop(learning_rate=0.001)
else:
opt = keras.optimizers.Adam(learning_rate=0.001)
self.model.compile(
optimizer=opt,
loss='sparse_categorical_crossentropy',
metrics=['accuracy']
)
#訓練模型並保存訓練歷史
start_time = time.time()
self.history = self.model.fit(
self.X,
self.y,
epochs=self.epochs,
batch_size=self.batch_size,
validation_split=0.2,
verbose=0
)
self.training_time = time.time() - start_time
def plot_training_history(self, ax1, ax2, label):
history_dict = self.history.history
epochs = range(1, len(history_dict['accuracy']) + 1)
#準確率曲線
ax1.plot(epochs, history_dict['accuracy'], 'o-', label=f'{label}訓練準確率', alpha=0.7)
ax1.plot(epochs, history_dict['val_accuracy'], 's--', label=f'{label}驗證準確率', alpha=0.7)
#損失曲線
ax2.plot(epochs, history_dict['loss'], 'o-', label=f'{label}訓練損失', alpha=0.7)
ax2.plot(epochs, history_dict['val_loss'], 's--', label=f'{label}驗證損失', alpha=0.7)
#最終指標
final_train_acc = history_dict['accuracy'][-1]
final_val_acc = history_dict['val_accuracy'][-1]
final_train_loss = history_dict['loss'][-1]
final_val_loss = history_dict['val_loss'][-1]
print(f"\n{label}優化器結果:")
print(f" 訓練準確率: {final_train_acc:.4f}")
print(f" 驗證準確率: {final_val_acc:.4f}")
print(f" 訓練損失: {final_train_loss:.4f}")
print(f" 驗證損失: {final_val_loss:.4f}")
print(f" 訓練時間: {self.training_time:.2f}秒")
def evaluate(self, X, y):
test_loss, test_acc = self.model.evaluate(X, y, verbose=0)
print(f" 測試集準確率: {test_acc:.4f}")
print(f" 測試集損失: {test_loss:.4f}")
return test_loss, test_acc
def predict(self, X):
predictions = self.model.predict(X, verbose=0)
predicted_classes = np.argmax(predictions, axis=1)
return predicted_classes
def compare_optimizers(X_train, y_train, X_test, y_test, epochs=10, batch_size=64):
"""比較不同優化器的性能"""
optimizers = ['sgd', 'momentum', 'adam', 'rmsprop']
optimizer_names = ['SGD', 'Momentum', 'Adam', 'RMSprop']
colors = ['blue', 'green', 'red', 'purple']
# 創建畫布
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 5))
trained_models = {}
cnn_template = CNN()
print("開始比較不同優化器...")
for opt, name, color in zip(optimizers, optimizer_names, colors):
print(f"\n訓練 {name} 優化器...")
#創建新的模型實例
model = cnn_template.get_model()
trained_model = TrainCNN(
model=model,
X=X_train,
y=y_train,
optimizer=opt,
epochs=epochs,
batch_size=batch_size
)
#存儲訓練好的模型
trained_models[name] = trained_model
#繪製收斂曲線
trained_model.plot_training_history(ax1, ax2, name)
ax1.set_title('不同優化器的準確率對比')
ax1.set_xlabel('Epochs')
ax1.set_ylabel('準確率')
ax1.legend()
ax1.grid(True, alpha=0.3)
ax2.set_title('不同優化器的損失對比')
ax2.set_xlabel('Epochs')
ax2.set_ylabel('損失')
ax2.legend()
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
print("\n" + "="*50)
print("測試集性能對比:")
print("="*50)
test_results = {}
for name, model in trained_models.items():
print(f"\n{name}優化器:")
test_loss, test_acc = model.evaluate(X_test, y_test)
test_results[name] = {
'test_accuracy': test_acc,
'test_loss': test_loss,
'training_time': model.training_time
}
#測試集性能對比圖
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
#測試準確率對比
names = list(test_results.keys())
accuracies = [test_results[name]['test_accuracy'] for name in names]
times = [test_results[name]['training_time'] for name in names]
bars1 = ax1.bar(names, accuracies, color=colors, alpha=0.7)
ax1.set_title('測試集準確率對比')
ax1.set_ylabel('準確率')
ax1.grid(True, alpha=0.3)
for bar, acc in zip(bars1, accuracies):
height = bar.get_height()
ax1.text(bar.get_x() + bar.get_width()/2., height + 0.01,
f'{acc:.4f}', ha='center', va='bottom')
#訓練時間對比
bars2 = ax2.bar(names, times, color=colors, alpha=0.7)
ax2.set_title('訓練時間對比')
ax2.set_ylabel('時間 (秒)')
ax2.grid(True, alpha=0.3)
for bar, t in zip(bars2, times):
height = bar.get_height()
ax2.text(bar.get_x() + bar.get_width()/2., height + 0.1,
f'{t:.2f}s', ha='center', va='bottom')
plt.tight_layout()
plt.show()
return trained_models, test_results
def plot_sample_predictions_comparison(models, X_test, y_test, num_samples=5):
"""比較不同模型在相同樣本上的預測結果"""
n_models = len(models)
fig, axes = plt.subplots(n_models, num_samples, figsize=(15, 3*n_models))
if n_models == 1:
axes = [axes]
for i, (name, model_obj) in enumerate(models.items()):
predicted_classes = model_obj.predict(X_test[:num_samples])
for j in range(num_samples):
ax = axes[i][j] if n_models > 1 else axes[j]
ax.imshow(X_test[j].reshape(28, 28), cmap='gray')
#正確為綠色,錯誤為紅色
color = 'green' if predicted_classes[j] == y_test[j] else 'red'
ax.set_title(f'{name}\n預測: {predicted_classes[j]}\n真實: {y_test[j]}',
color=color, fnotallow=10)
ax.axis('off')
plt.tight_layout()
plt.show()
if __name__ == '__main__':
plt.rcParams['font.sans-serif'] = ['WenQuanYi Micro Hei']
plt.rcParams['axes.unicode_minus'] = False
(x_train, y_train), (x_test, y_test) = keras.datasets.mnist.load_data()
x_train = x_train.reshape((60000, 28, 28, 1))
x_test = x_test.reshape((10000, 28, 28, 1))
X_train = x_train.astype('float32') / 255.0
X_test = x_test.astype('float32') / 255.0
#比較不同優化器
trained_models, test_results = compare_optimizers(
X_train, y_train, X_test, y_test, epochs=10, batch_size=64
)
#最佳模型
best_optimizer = max(test_results.items(), key=lambda x: x[1]['test_accuracy'])
print(f"\n最佳優化器: {best_optimizer[0]}, 測試準確率: {best_optimizer[1]['test_accuracy']:.4f}")
#比較不同模型在相同樣本上的預測
print("\n不同優化器在相同樣本上的預測對比:")
plot_sample_predictions_comparison(trained_models, X_test, y_test, num_samples=5)