當你走進一家咖啡館,看到一個朋友面前放着半杯咖啡。
經典統計學家可能會説:根據歷史數據,80%的人在這裏點美式咖啡。
而貝葉斯主義者:讓我用新證據更新一下我的信念,既然杯子只有半滿,説明他可能剛來不久,而且眉頭微皺,可能咖啡不太合口味...
貝葉斯定理的數學表達式:
翻譯成人話就是:新證據出現後,我對某個假設的信念需要更新。其中P(A)是先驗概率(原來的信念),P(B|A)是似然(假設成立時看到證據的可能性),P(A|B)是後驗概率(看到證據後更新的信念)。
歷史發展
貝葉斯定理的創始人托馬斯·貝葉斯可謂生前寂寂無名,死後眾人崇拜的典型。
這位18世紀的英國統計學家在1763年去世後,他的朋友才將他的論文發表出來。
可悲的是,當時這工作幾乎石沉大海。
直到法國數學家拉普拉斯重新發現並完善了這個理論,貝葉斯公式才開始嶄露頭角。
但即使如此,在其後的兩百年間,它仍然是統計學界的非主流,頻率主義統計才是當時的王者。
貝葉斯定理的逆襲之路:
- 18世紀:貝葉斯提出基本思想,拉普拉斯完善公式
- 二戰期間:被用於密碼破譯和軍事決策,開始展現實用價值
- 20世紀後期:隨着計算機科學發展,在人工智能領域大放異彩
- 21世紀大數據時代:成為機器學習、數據挖掘的核心工具之一
有趣的是,貝葉斯定理的崛起與大數據發展幾乎是同步的。
這不禁讓我想起自己在讀書研究中的體會:當數據足夠多時,先驗信念的影響力會逐漸減弱,數據自己會説話。
機器學習中的貝葉斯
1. 樸素貝葉斯分類器:簡單卻強大
雖然名字叫樸素,因為它假設特徵之間相互獨立,但這個算法在文本分類、垃圾郵件過濾等領域表現驚人。
比如垃圾郵件過濾:算法會計算每個單詞在垃圾郵件和正常郵件中出現的概率,然後根據貝葉斯公式組合這些信息。
當你收到一封包含免費、贏取、獎金等詞的郵件時,系統會計算P(垃圾郵件|這些詞),從而做出判斷。
2. 語音識別:貝葉斯的聽覺系統
著名科學家賈里尼克將語音識別問題轉化為一個貝葉斯推斷問題:給定聲音信號,推測最可能對應的文字序列。
這種思路打破了之前基於語法規則的方法的瓶頸,讓Siri、小愛同學等智能助手成為可能。
3. 貝葉斯深度學習
傳統的深度學習模型像黑盒子,而貝葉斯深度學習則試圖將概率思維引入神經網絡,提供不確定性估計和更好的可解釋性。這在醫療診斷、自動駕駛等需要高可靠性的領域尤為重要。
代碼實現
代碼感受貝葉斯思維~
現在,讓我們動手實現一個簡單的貝葉斯分類器。
使用手寫數字識別作為例子,也是機器學習入門的經典案例。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix
import seaborn as sns
# 加載手寫數字數據集(8x8像素的數字圖像)
digits = load_digits()
X = digits.data # 特徵向量(64維)
y = digits.target # 標籤(0-9)
print(f'數據集形狀: {X.shape}')
print(f'樣本數量: {len(y)}')
print(f'數字類別: {np.unique(y)}')
# 劃分訓練集和測試集
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=42
)
# 創建並訓練樸素貝葉斯模型
model = GaussianNB()
model.fit(X_train, y_train)
# 預測測試集
y_pred = model.predict(X_test)
# 計算準確率
accuracy = accuracy_score(y_test, y_pred)
print(f'\n模型準確率: {accuracy:.4f}')
# 可視化部分預測結果
plt.figure(figsize=(12, 8))
# 顯示前10個測試樣本的預測結果
for i in range(10):
plt.subplot(2, 5, i + 1)
plt.imshow(X_test[i].reshape(8, 8), cmap=plt.cm.gray_r)
prediction = y_pred[i]
true_label = y_test[i]
color = 'green'if prediction == true_label else'red'
plt.title(f'真實: {true_label}, 預測: {prediction}', color=color, fontsize=12)
plt.axis('off')
plt.suptitle('手寫數字識別結果(綠色正確,紅色錯誤)', fontsize=14)
plt.tight_layout()
plt.show()
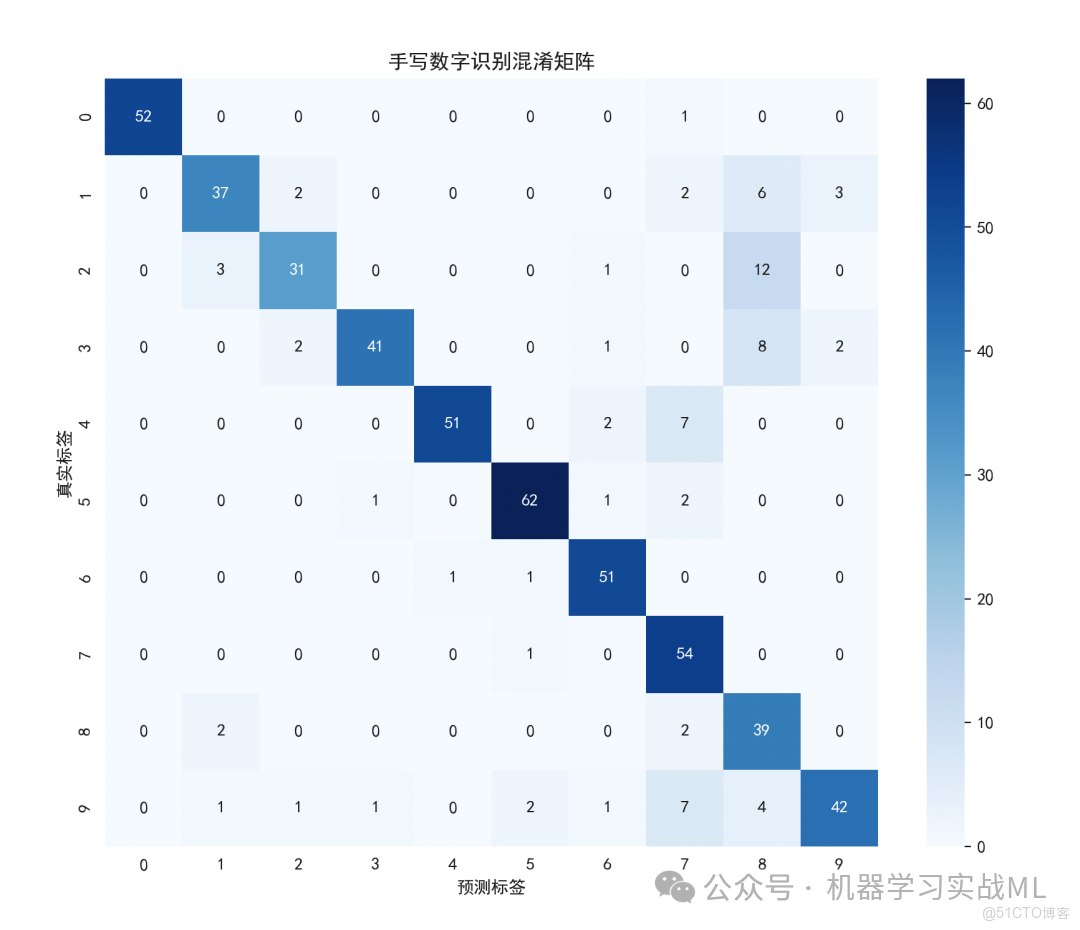
# 繪製混淆矩陣熱力圖
plt.figure(figsize=(10, 8))
cm = confusion_matrix(y_test, y_pred)
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues',
xticklabels=range(10), yticklabels=range(10))
plt.xlabel('預測標籤')
plt.ylabel('真實標籤')
plt.title('手寫數字識別混淆矩陣')
plt.show()
# 輸出詳細分類報告
print('\n分類報告:')
print(classification_report(y_test, y_pred))
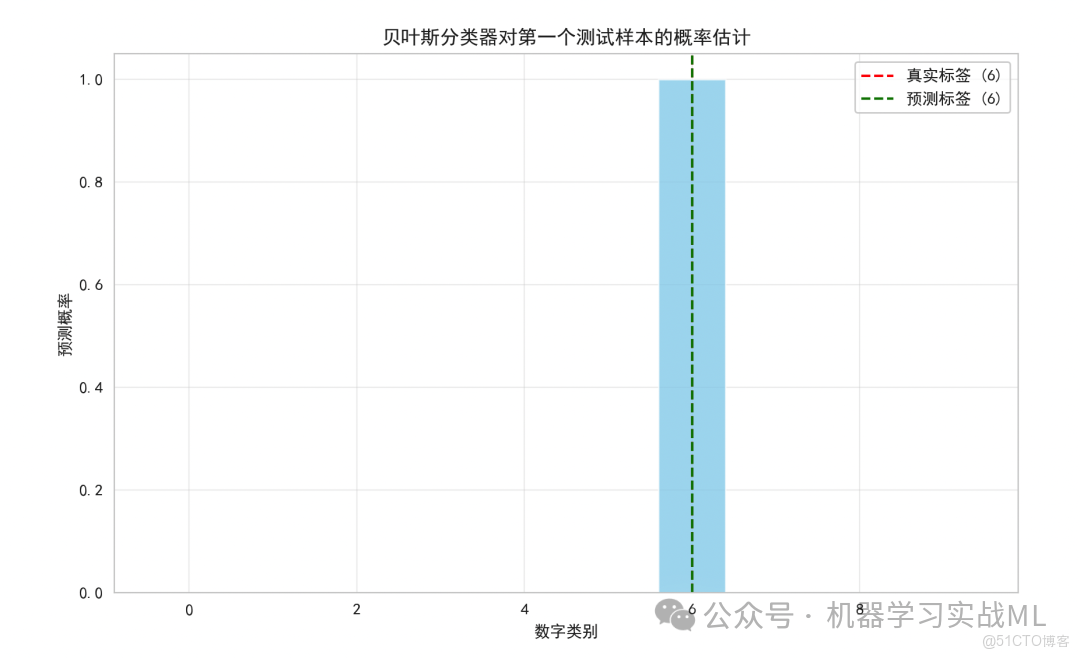
# 可視化貝葉斯概率估計過程(以第一個測試樣本為例)
first_sample = X_test[0:1]
predicted_probabilities = model.predict_proba(first_sample)
plt.figure(figsize=(10, 6))
classes = range(10)
plt.bar(classes, predicted_probabilities[0], color='skyblue', alpha=0.7)
plt.axvline(x=y_test[0], color='red', linestyle='--', label=f'真實標籤 ({y_test[0]})')
plt.axvline(x=y_pred[0], color='green', linestyle='--', label=f'預測標籤 ({y_pred[0]})')
plt.xlabel('數字類別')
plt.ylabel('預測概率')
plt.title('貝葉斯分類器對第一個測試樣本的概率估計')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()1.手寫數字的圖像及其識別結果(綠色表示正確,紅色表示錯誤)
2.混淆矩陣熱力圖,顯示模型在各類別上的表現
3.貝葉斯分類器對每個類別的概率估計可視化
- 我們使用高斯樸素貝葉斯分類器,它假設每個特徵服從正態分佈
- 模型會計算每個數字類別的先驗概率
P(數字) - 對於新樣本,計算後驗概率
P(數字|像素特徵) - 選擇後驗概率最大的數字作為預測結果