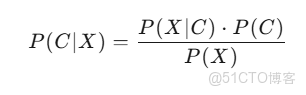貝葉斯網絡(Bayesian Network)介紹
1. 基本概念
貝葉斯網絡(Bayesian Network)是一種有向無環圖(DAG),用於表示變量之間的條件依賴關係。它結合了概率論和圖論,能夠以直觀的方式表示變量之間的概率關係,並通過圖形結構進行高效的推理和計算。貝葉斯網絡的核心是利用貝葉斯定理進行概率推理。
2. 組成要素
貝葉斯網絡主要由以下幾個部分組成:
- 節點(Nodes):表示隨機變量,可以是離散的或連續的。
- 有向邊(Directed Edges):表示變量之間的條件依賴關係,從父節點指向子節點。
- 條件概率分佈(Conditional Probability Distributions, CPDs):每個節點都有一個條件概率分佈,表示在給定其父節點值的情況下該節點的分佈。
3. 貝葉斯定理
貝葉斯定理是貝葉斯網絡的核心,用於計算後驗概率:
編輯
其中:
- P(C∣X) 是在特徵 X 出現的條件下,類別 C 出現的概率(後驗概率)。
- P(X∣C) 是在類別 C 出現的條件下,特徵 X 出現的概率(似然概率)。
- P(C) 是類別 C 出現的先驗概率。
- P(X) 是特徵 X 出現的先驗概率。
4. 推理算法
貝葉斯網絡中的推理是指計算給定證據下的後驗概率。常見的推理算法包括:
- 變量消除(Variable Elimination):通過消除無關變量來簡化計算。
- 信念傳播(Belief Propagation):在無向圖上進行高效的推理。
- 蒙特卡洛方法(Monte Carlo Methods):通過隨機抽樣進行近似推理。
貝葉斯網絡代碼示例
以下是一個使用 Python 和 pgmpy 庫實現的貝葉斯網絡的代碼示例:
Python
Copy
from pgmpy.models import BayesianNetwork
from pgmpy.factors.discrete import TabularCPD
from pgmpy.inference import VariableElimination
# 定義貝葉斯網絡結構
model = BayesianNetwork([('W', 'S'), ('W', 'G'), ('S', 'G')])
# 定義條件概率分佈
cpd_w = TabularCPD(variable='W', variable_card=2, values=[[0.7], [0.3]], state_names={'W': ['sunny', 'rain']})
cpd_s = TabularCPD(variable='S', variable_card=2, values=[[0.9, 0.1], [0.1, 0.9]], evidence=['W'], evidence_card=[2], state_names={'W': ['sunny', 'rain'], 'S': ['on', 'off']})
cpd_g = TabularCPD(variable='G', variable_card=2, values=[[0.99, 0.9, 0.8, 0.01], [0.01, 0.1, 0.2, 0.99]], evidence=['W', 'S'], evidence_card=[2, 2], state_names={'W': ['sunny', 'rain'], 'S': ['on', 'off'], 'G': ['dry', 'wet']})
# 將條件概率分佈添加到模型中
model.add_cpds(cpd_w, cpd_s, cpd_g)
# 檢查模型是否有效
assert model.check_model()
# 推理
inference = VariableElimination(model)
result = inference.query(variables=['G'], evidence={'W': 'sunny', 'S': 'on'})
print(result)
代碼説明
- 定義貝葉斯網絡結構:
- 使用
BayesianNetwork定義網絡結構,指定節點之間的有向邊。
- 定義條件概率分佈:
- 使用
TabularCPD定義每個節點的條件概率分佈。 variable_card表示變量的取值數量。values表示條件概率表。evidence和evidence_card表示父節點及其取值數量。
- 添加條件概率分佈:
- 使用
add_cpds方法將條件概率分佈添加到模型中。
- 檢查模型:
- 使用
check_model方法檢查模型是否有效。
- 推理:
- 使用
VariableElimination進行推理,計算給定證據下的目標變量的後驗概率。
貝葉斯網絡的應用
1. 醫療診斷
- 應用背景:在醫療診斷中,貝葉斯網絡可以用於表示症狀、疾病和檢查結果之間的關係。
- 方法:通過貝葉斯網絡,可以計算在給定症狀和檢查結果的情況下,患者患有某種疾病的概率。
- 結果:提高診斷的準確性和效率。
2. 金融風險評估
- 應用背景:在金融領域,貝葉斯網絡可以用於評估金融風險。
- 方法:通過貝葉斯網絡,可以計算在給定市場條件和交易數據的情況下,某個金融產品違約的概率。
- 結果:提高風險評估的準確性和可靠性。
3. 自然語言處理
- 應用背景:在自然語言處理中,貝葉斯網絡可以用於表示文本中的詞彙和句子之間的關係。
- 方法:通過貝葉斯網絡,可以進行情感分析、機器翻譯和問答系統等任務。
- 結果:提高自然語言處理的準確性和效率。
4. 圖像處理
- 應用背景:在圖像處理中,貝葉斯網絡可以用於表示圖像中的像素之間的關係。
- 方法:通過貝葉斯網絡,可以進行圖像分割、去噪和超分辨率等任務。
- 結果:提高圖像處理的質量和效率。
總結
貝葉斯網絡是一種強大的工具,能夠以直觀的方式表示變量之間的概率關係,並通過圖形結構進行高效的推理和計算。它在醫療診斷、金融風險評估、自然語言處理和圖像處理等領域有廣泛的應用。通過上述代碼示例,你可以快速實現一個貝葉斯網絡,並在實際任務中進行應用。