線性變換的矩陣表示
背景知識
在線性代數中,線性變換是指滿足以下兩個條件的變換
(可加性)
(齊次性)
對於任意向量

線性變換的矩陣表示:給定線性變換





在 
線性變換的矩陣表示基本原理
線性變換的矩陣表示基於一個核心思想:矩陣的列就是標準基向量經過變換後的座標。
標準基的重要性
在 
這些基向量的重要性在於:
- 任何向量
都可以表示為
- 如果大家知道每個基向量
經過變換
後的結果,就能確定任意向量
矩陣-向量乘法的列視角
考慮矩陣 

這個公式表明:
- 矩陣
的第
列就是
- 矩陣-向量乘法實際上是輸入向量各分量與矩陣各列的線性組合
題目求解
(1) 關於
變換規則:
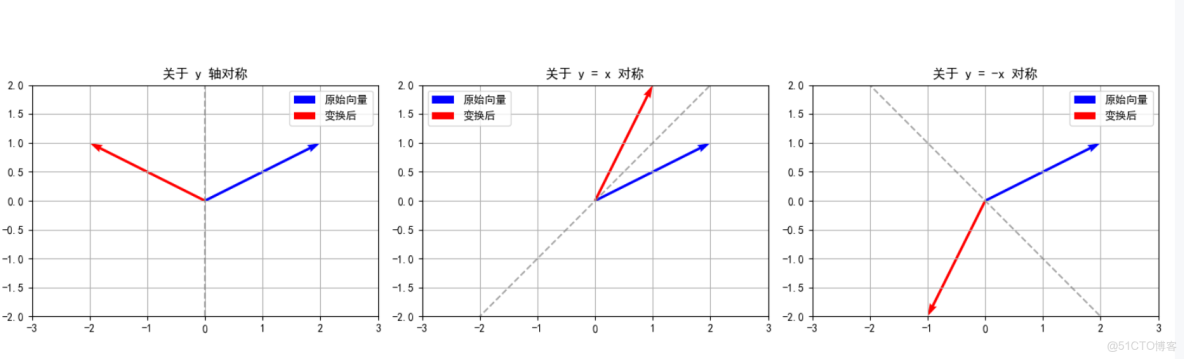
關於 y 軸對稱時,x 座標取反,y 座標不變
計算標準基的變換:
矩陣表示:
驗證:
(2) 關於直線
變換規則:
關於直線 y=x對稱時,x 和 y 座標交換
計算標準基的變換:
矩陣表示:
驗證:
(3) 關於直線
變換規則:
關於直線 y=−x 對稱時,x 座標變為 -y,y 座標變為 -x
計算標準基的變換:
矩陣表示:
驗證:
圖表
|
變換類型
|
矩陣表示
|
|
關於 |
|
|
關於 |
|
|
關於 |
|
運行代碼可視化
python代碼
import numpy as np
import matplotlib.pyplot as plt
# 設置中文字體
plt.rcParams['font.sans-serif'] = ['SimHei'] # 解決中文顯示問題-設置字體為黑體
plt.rcParams['axes.unicode_minus'] = False # 解決保存圖像是負號'-'顯示為方塊的問題
# 定義標準基向量
e1 = np.array([1, 0])
e2 = np.array([0, 1])
print("標準基向量:")
print(f"e1 = {e1}")
print(f"e2 = {e2}")
print()
# (1) 關於 y 軸對稱的變換
def reflection_y(vec):
"""關於 y 軸對稱變換"""
return np.array([-vec[0], vec[1]])
# 計算標準基的變換結果
T_e1_y = reflection_y(e1)
T_e2_y = reflection_y(e2)
# 構建變換矩陣
A_y = np.column_stack([T_e1_y, T_e2_y])
print("(1) 關於 y 軸對稱的變換矩陣:")
print(A_y)
# (2) 關於直線 y = x 對稱的變換
def reflection_y_eq_x(vec):
"""關於直線 y = x 對稱變換"""
return np.array([vec[1], vec[0]])
# 計算標準基的變換結果
T_e1_yx = reflection_y_eq_x(e1)
T_e2_yx = reflection_y_eq_x(e2)
# 構建變換矩陣
A_yx = np.column_stack([T_e1_yx, T_e2_yx])
print("(2) 關於直線 y = x 對稱的變換矩陣:")
print(A_yx)
# (3) 關於直線 y = -x 對稱的變換
def reflection_y_eq_minus_x(vec):
"""關於直線 y = -x 對稱變換"""
return np.array([-vec[1], -vec[0]])
# 計算標準基的變換結果
T_e1_ymx = reflection_y_eq_minus_x(e1)
T_e2_ymx = reflection_y_eq_minus_x(e2)
# 構建變換矩陣
A_ymx = np.column_stack([T_e1_ymx, T_e2_ymx])
print("(3) 關於直線 y = -x 對稱的變換矩陣:")
print(A_ymx)
# 可視化變換結果
def plot_transformations():
"""繪製變換效果圖"""
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
# 原始向量
original = np.array([2, 1])
# (1) 關於 y 軸對稱
axes[0].quiver(0, 0, original[0], original[1], angles='xy', scale_units='xy', scale=1, color='blue',
label='原始向量')
transformed = A_y @ original
axes[0].quiver(0, 0, transformed[0], transformed[1], angles='xy', scale_units='xy', scale=1, color='red',
label='變換後')
axes[0].axvline(x=0, color='gray', linestyle='--', alpha=0.7)
axes[0].set_xlim(-3, 3)
axes[0].set_ylim(-2, 2)
axes[0].set_aspect('equal')
axes[0].set_title('關於 y 軸對稱')
axes[0].legend()
axes[0].grid(True)
# (2) 關於直線 y = x 對稱
axes[1].quiver(0, 0, original[0], original[1], angles='xy', scale_units='xy', scale=1, color='blue',
label='原始向量')
transformed = A_yx @ original
axes[1].quiver(0, 0, transformed[0], transformed[1], angles='xy', scale_units='xy', scale=1, color='red',
label='變換後')
x = np.linspace(-3, 3, 100)
axes[1].plot(x, x, 'gray', linestyle='--', alpha=0.7)
axes[1].set_xlim(-3, 3)
axes[1].set_ylim(-2, 2)
axes[1].set_aspect('equal')
axes[1].set_title('關於 y = x 對稱')
axes[1].legend()
axes[1].grid(True)
# (3) 關於直線 y = -x 對稱
axes[2].quiver(0, 0, original[0], original[1], angles='xy', scale_units='xy', scale=1, color='blue',
label='原始向量')
transformed = A_ymx @ original
axes[2].quiver(0, 0, transformed[0], transformed[1], angles='xy', scale_units='xy', scale=1, color='red',
label='變換後')
axes[2].plot(x, -x, 'gray', linestyle='--', alpha=0.7)
axes[2].set_xlim(-3, 3)
axes[2].set_ylim(-2, 2)
axes[2].set_aspect('equal')
axes[2].set_title('關於 y = -x 對稱')
axes[2].legend()
axes[2].grid(True)
plt.tight_layout()
plt.show()
# 執行可視化
plot_transformations()