本專題主要參考《Principles of Magnetic Resonance Imaging A Signal Processing Perspective 》-Sec 9.3

回波平面成像

回波平面成像（Echo-Planar Imaging, EPI）是曼斯菲爾德於1977年提出的首種超高速成像技術。此後發展出多種變體。如今該術語廣泛指代在單次激發脈衝後的自由感應衰減期內採集"完整"二維編碼集的高速成像方法類別。因此，EPI已成為單次激造成像的同義詞，儘管具有交錯k空間覆蓋的多激發EPI方法也常用。

EPI的關鍵概念是利用時變梯度遍歷k空間。接下來討論三種流行的k空間軌跡：Z字形軌跡、直線軌跡和螺旋軌跡。

Z字形軌跡

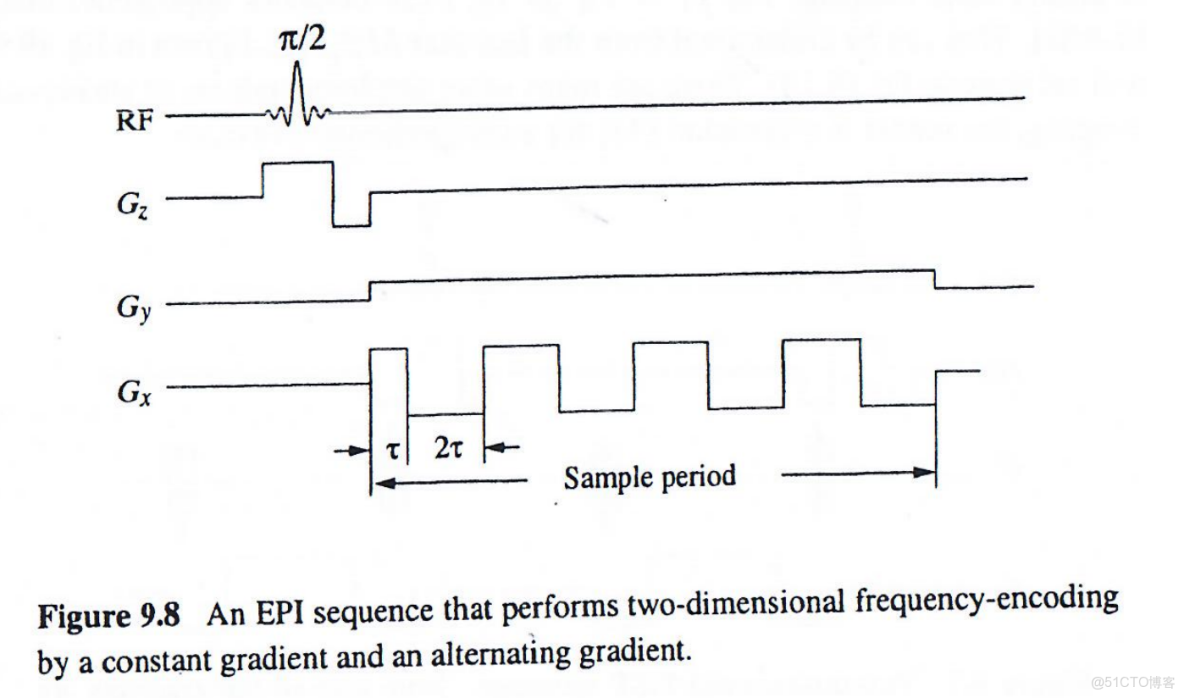
為理解單次激發下的k空間覆蓋，首先考慮曼斯菲爾德提出的原始EPI方法（圖9.8）。該成像方案在讀出期間使用一對頻率編碼梯度：小型恆定梯度和快速交變梯度。交變梯度在自由進動期間產生一系列梯度回波，從而實現快速成像。

根據k空間定義：

上圖9.8所展示的序列對應的k空間編碼為：

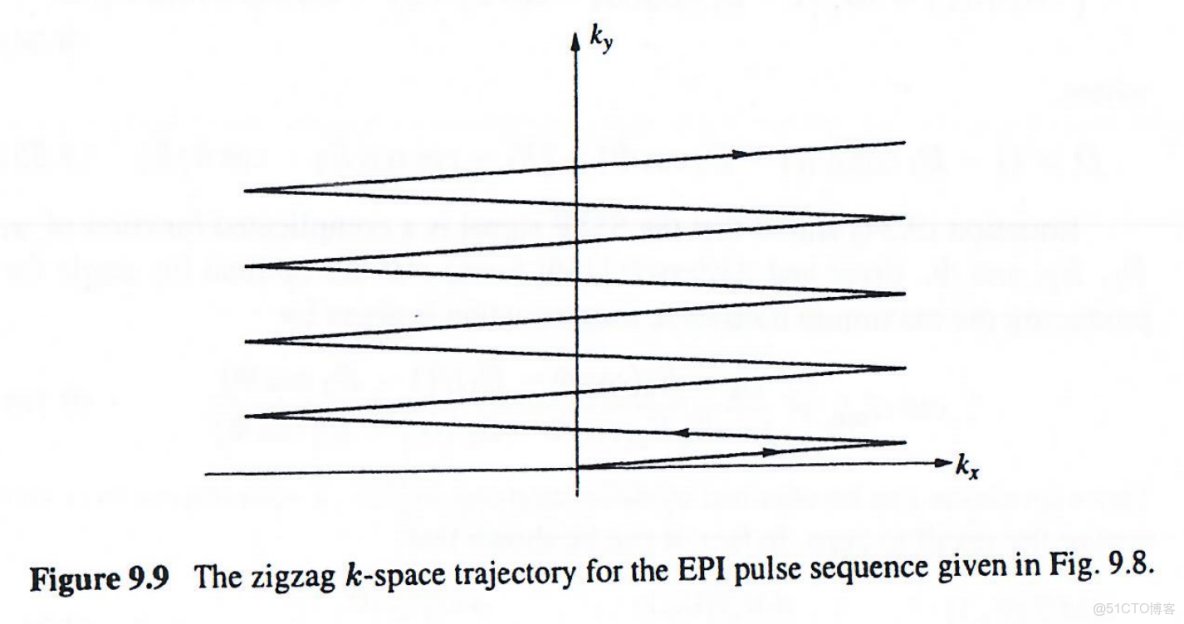
因此，該序列產生的每個梯度回波被映射到傾斜的k空間線，形成下圖9.9所示的Z字形軌跡。注意該軌跡僅覆蓋k空間上半部分。為獲得全k空間覆蓋，需形成自旋迴波或梯度回波。

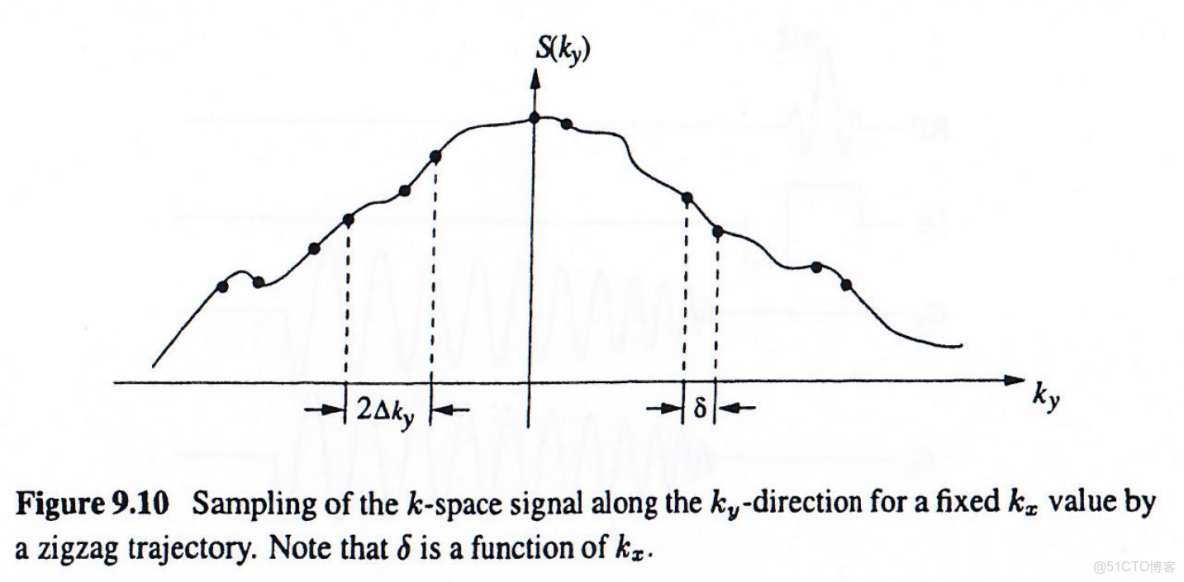
Z字形軌跡的實際問題是需要特殊圖像重建算法，因為沿方向的採樣是非均勻的。解決方法之一是使用交錯採樣理論。具體而言，固定值時，沿軸的信號變化可表示為，其採樣如圖9.10所示。

將採樣點分為奇偶索引序列：

在理想無限採樣下，回憶式子(6.10)如下


根據式子(6.10)，將，奇索引的傅里葉重建結果為：

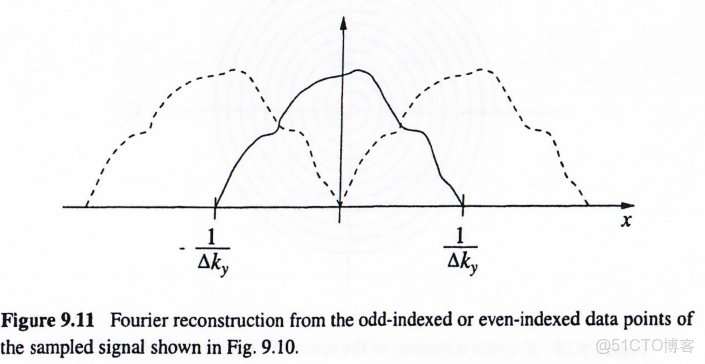
偶索引的傅里葉重建結果為：

當取奈奎斯特採樣間隔時，和會產生混疊偽影（圖9.11）。但在特定區間內可通過代數運算消除：

對於區間：

對於區間：

通過簡單代數運算可得解混疊公式：

實際有限採樣時，和可用常規FFT算法重建，再按式子(9.51)重組得到。

直線軌跡

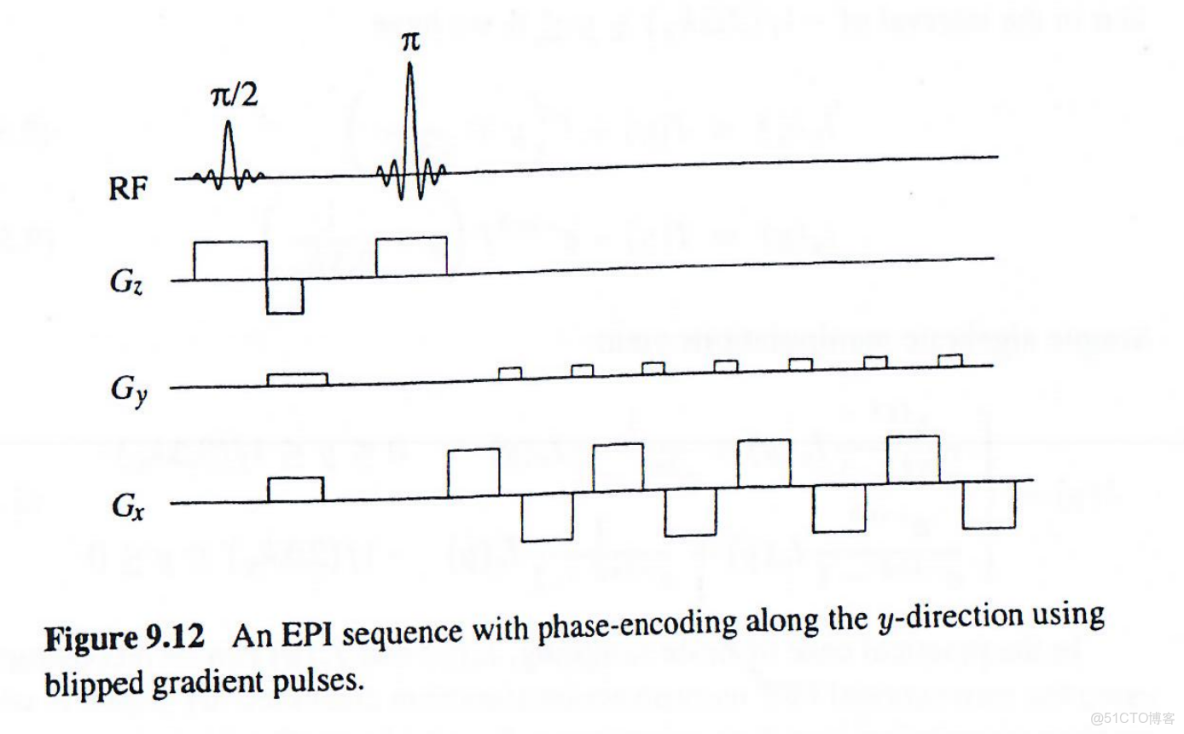
Pykett和Rzedzian（1987）提出的EPI序列可實現k空間正交採樣（圖9.12）。該序列使用系列blipped 脈衝對單個梯度回波進行相位編碼。與傳統成像不同，此處相位編碼梯度幅度恆定，無需遞增步進，因為橫向磁化會累積每個相位編碼blip引入的相位分散。這種相位累積效應在傳統成像中不會發生，因為每個相位編碼步會生成新的橫向磁化。

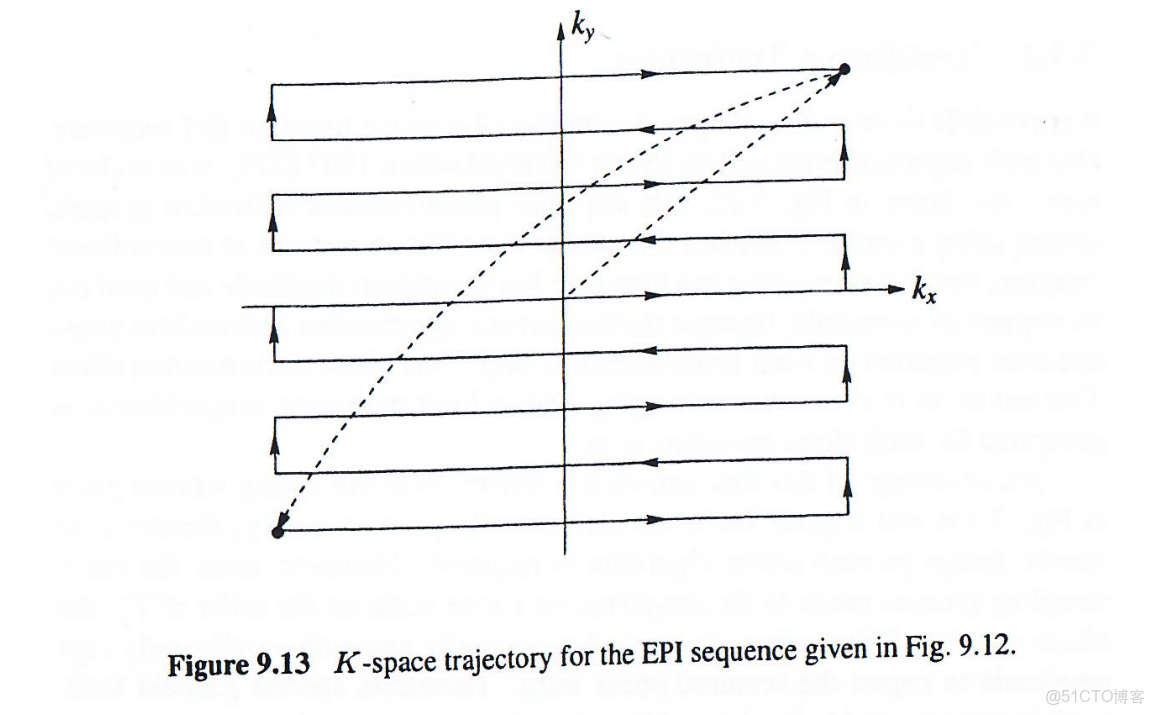
該方案相比Z字形軌跡的優勢是產生常規直線k空間軌跡（圖9.13），無需特殊重建算法。但由於整個採樣過程需在T2時間尺度內完成，相位編碼blip需快速施加且幅度足夠高，因此常需特殊梯度硬件（要求快速切換，需要梯度電流帶寬要求較高）實現。

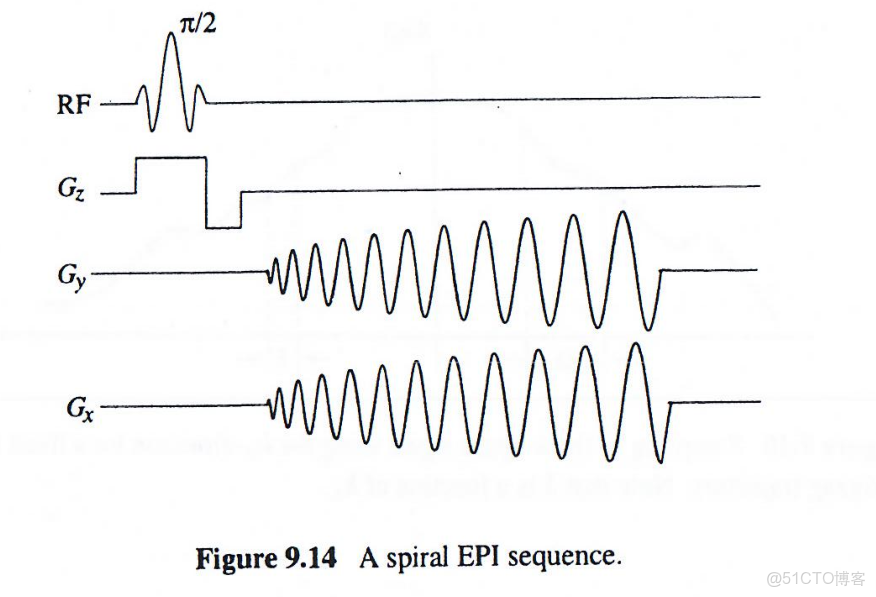
螺旋軌跡

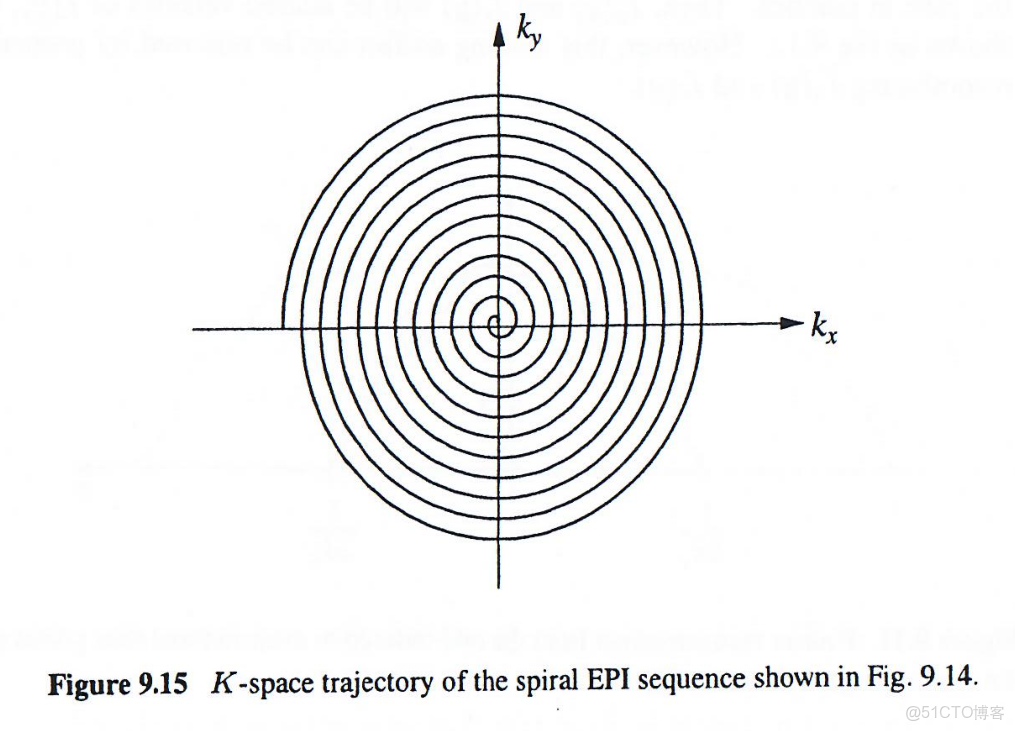
圖9.14所示的單次成像方法對梯度硬件要求較低。該方法使用一對遞增正弦梯度以螺旋方式遍歷k空間（圖9.15），稱為螺旋成像。該方法完全消除了先前序列所需的快速梯度切換。

螺旋軌跡的數學表達式為：

其中，和是時間函數。螺旋序列設計的關鍵步驟是角速度函數選擇。例如：

對應k空間軌跡為：

或簡化為：

根據k空間定義：

所需梯度函數為：

其中。對應梯度通道為：

該梯度對定義的螺旋路徑具有恆定角速度（公式9.55所示），意味着k空間中心區域耗時比外圍多。實際上，由於梯度強度限制，外圍區域的掃描速度可能過大。該問題可通過恆定線速度螺旋軌跡克服，例如設：

對應地：

且：

在k空間外圍區域（t較大時）：

意味着G(t)幅度變為常數。

該梯度函數的問題是在t=0處有極點，實際中因梯度強度和上升時間限制難以實現。更實用的螺旋軌跡定義為：

其中為時間參數，使在t≪T時具恆定角速度，t≫T時具恆定線速度。

螺旋軌跡數據需要特殊圖像重建算法。實踐中常用數據插值方案將螺旋數據映射到矩形網格，再用常規傅里葉重建算法處理。使用方形螺旋軌跡可減輕插值問題，僅需一維插值。

討論

當前梯度技術下，EPI方法可在約50ms內採集二維圖像，克服了生理運動引起的圖像退化問題。此外，單次EPI的有效無限長，產生具真實或對比度的圖像。

儘管有這些優勢，EPI方法仍有若干固有侷限。首先，最大可達分辨率受值限制。具體地，點擴散函數（PSF）可寫為：

雖然該PSF沿讀出方向可忽略，但在其他方向可能導致顯著模糊，因為數據採集時間遠大於。此外，EPI圖像可能因偏共振效應和梯度誤差產生明顯偽影。