目錄
一、引言
二、什麼是優先級隊列?
2.1 基本概念
三、堆:優先級隊列的底層實現
3.1 堆的基本概念
3.1.1 堆的定義
3.1.2 堆的存儲
3.2 堆的核心操作
3.2.1 向下調整(Shift Down)
3.2.2 向上調整(Shift Up)
3.2.3 插入與刪除操作
四、Java中的PriorityQueue
4.1 基本特性
4.2 構造方法
4.3 自定義比較器
4.4 擴容機制
五、堆的實戰
5.1 堆排序
5.2 Top-K
一、引言
在計算機科學中,隊列
然而,在實際應用中,我們經常會遇到需要根據 優先級處理元素
比如操作系統中進程調度、遊戲中的事件處理、數據流中的高頻元素統計等,這些場景都需要優先級高的元素能夠優先被處理。
優先級隊列(Priority Queue)就是為解決這類問題而設計的數據結構。它不同於普通隊列的FIFO特性,而是根據元素的優先級進行出隊操作,優先級最高的元素總是最先出隊。
本文將深入探討優先級隊列的底層實現——堆(Heap),從基本概念到具體實現,從理論分析到實際應用,幫助讀者全面掌握這一重要數據結構。
二、什麼是優先級隊列?
2.1 基本概念
優先級隊列是一種抽象數據類型,它支持以下兩個基本操作:
- 插入(Insert):添加一個帶有優先級的元素
- 提取最高優先級(Extract-Max/Min):移除並返回優先級最高或最低的元素
與普通隊列相比,優先級隊列的出隊順序不是由元素的入隊時間決定,而是由元素的優先級決定。
三、堆:優先級隊列的底層實現
3.1 堆的基本概念
3.1.1 堆的定義
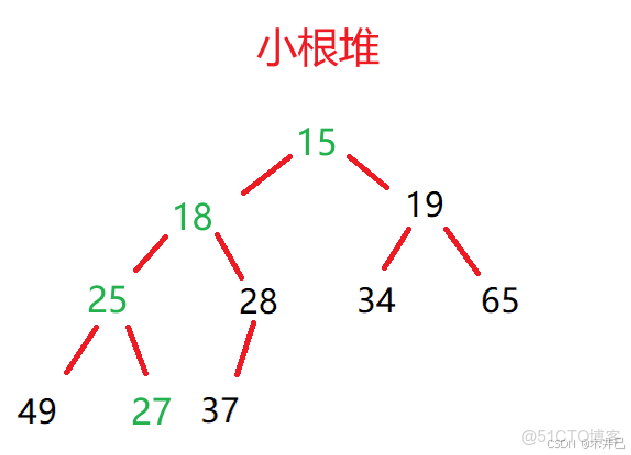
堆是一種特殊的完全二叉樹,它滿足以下性質:
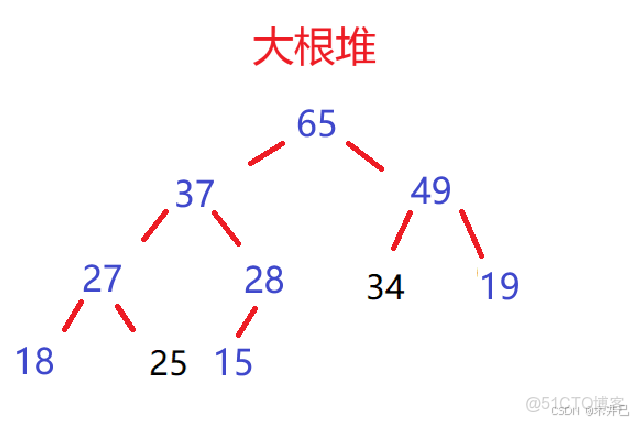
- 對於大根堆:每個節點的值都大於或等於其子節點的值
- 對於小根堆:每個節點的值都小於或等於其子節點的值
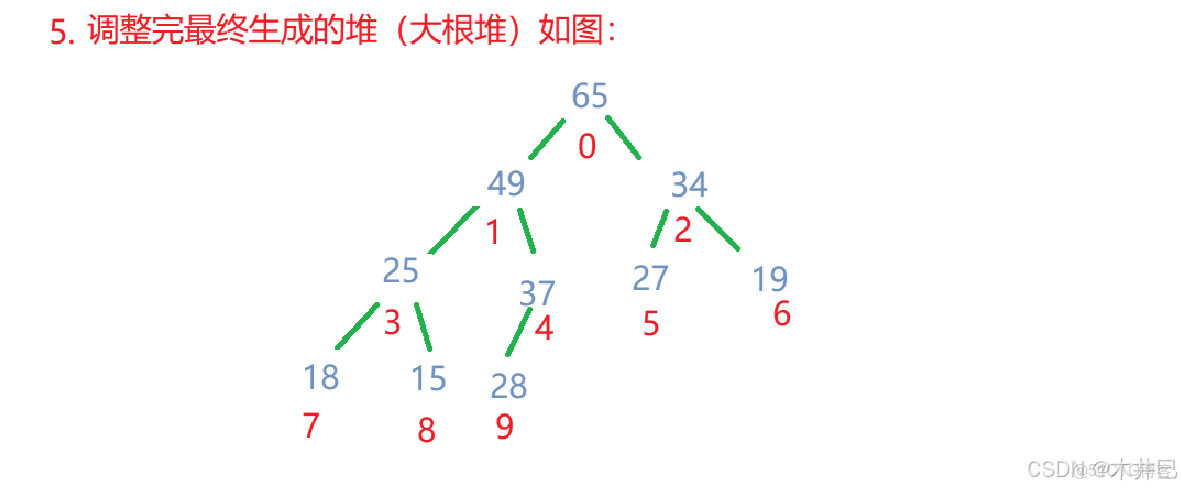
比如一組數據:27,15,19,18,28,34,65,49,25,37
根據這組數據建立的小根堆和大根堆如下圖:
3.1.2 堆的存儲
由於堆是完全二叉樹,我們可以使用數組來高效存儲,不需要使用指針。
這種存儲方式既節省空間,又能快速定位任意節點的父節點和子節點。
public class Heap {
public int[] elem; // 用數組存儲數據
public int usedSize; // 記錄堆的大小
public Heap() {
this.elem = new int[10];
}
}3.2 堆的核心操作
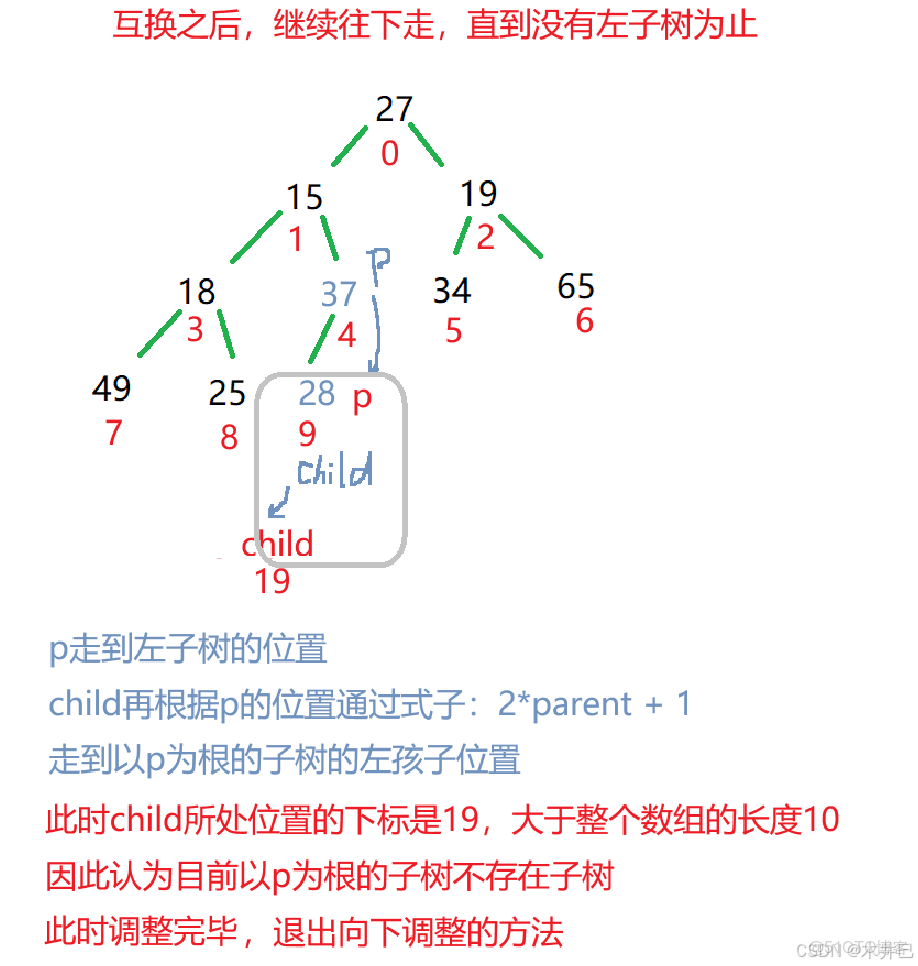
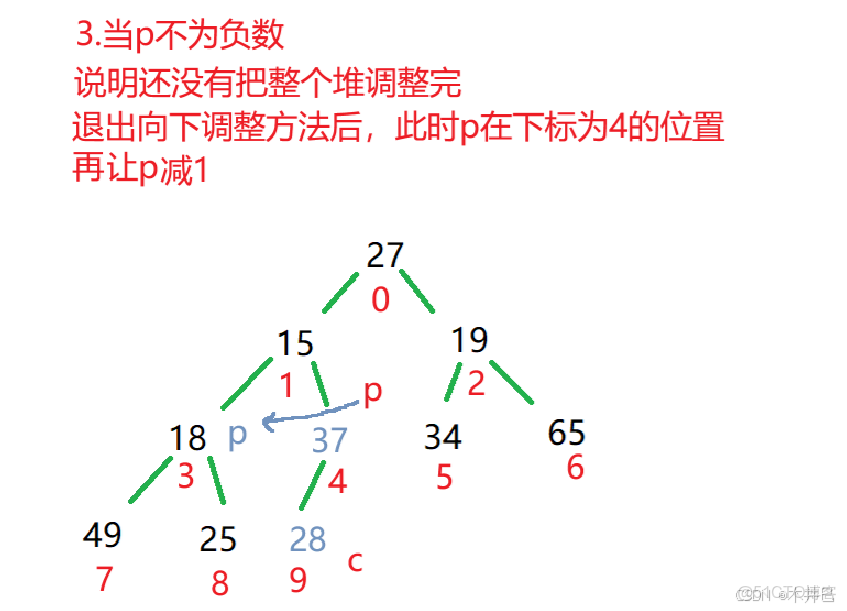
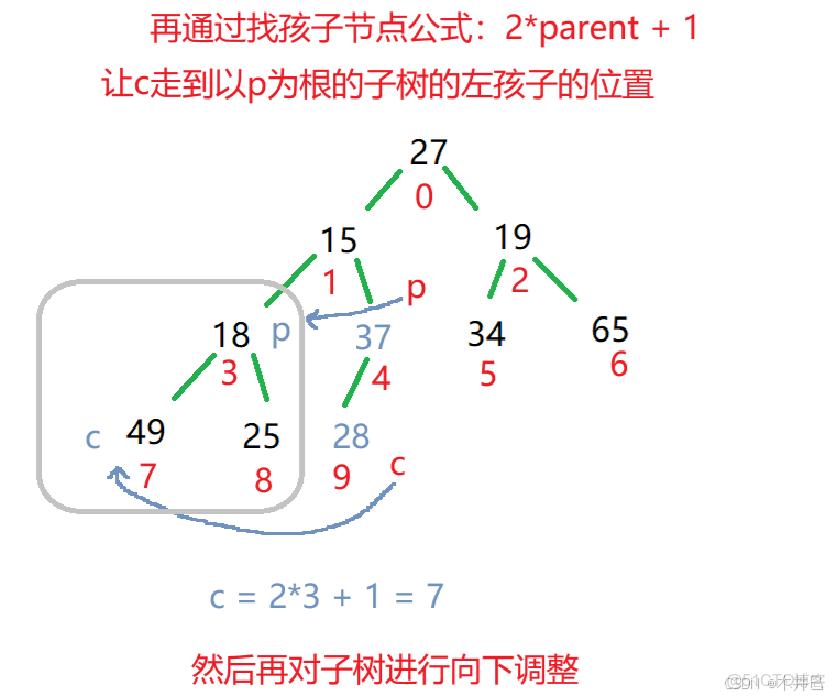
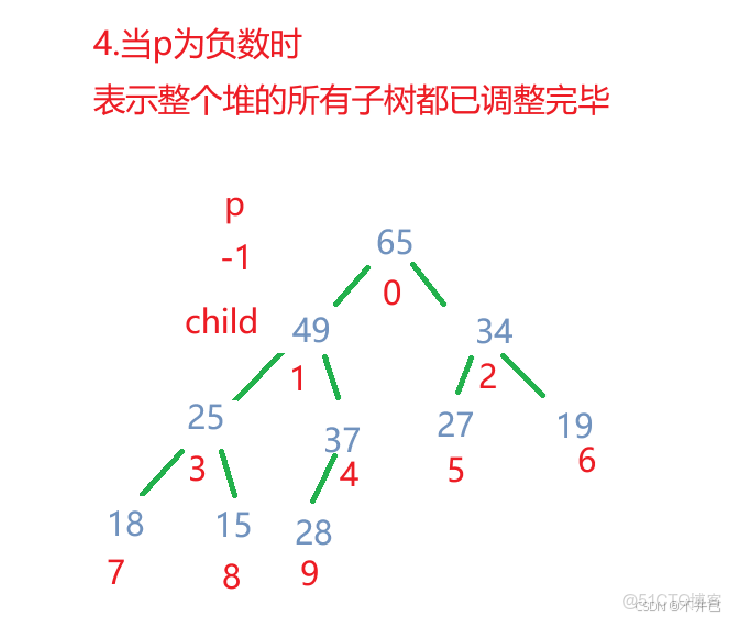
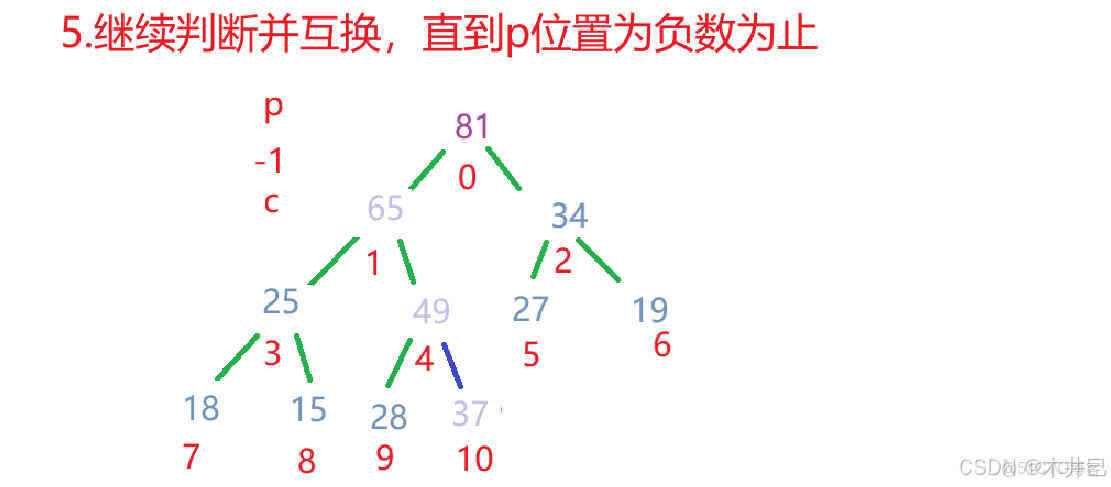
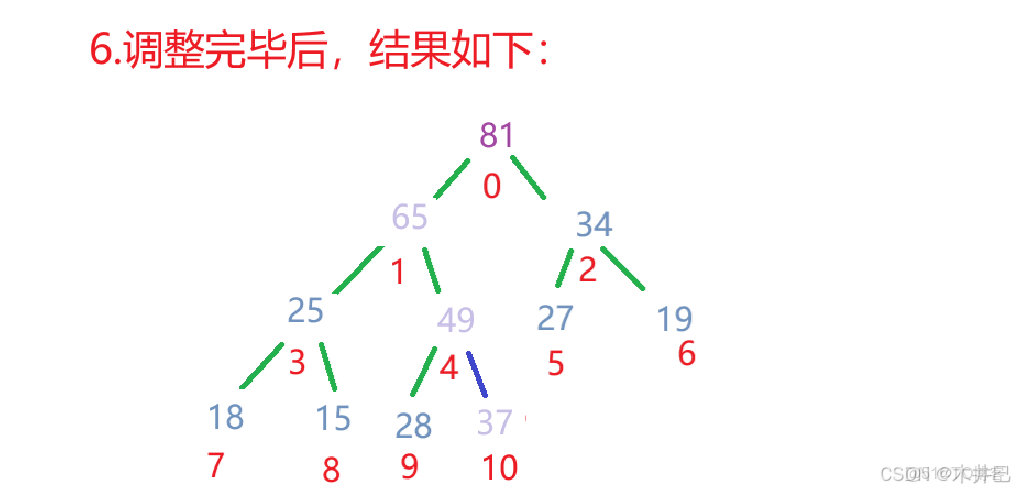
3.2.1 向下調整(Shift Down)
向下調整是堆的核心操作之一,用於維護堆的性質。
當某個節點的值發生變化(通常是變小在大根堆中或變大在小根堆中),可能需要向下調整。
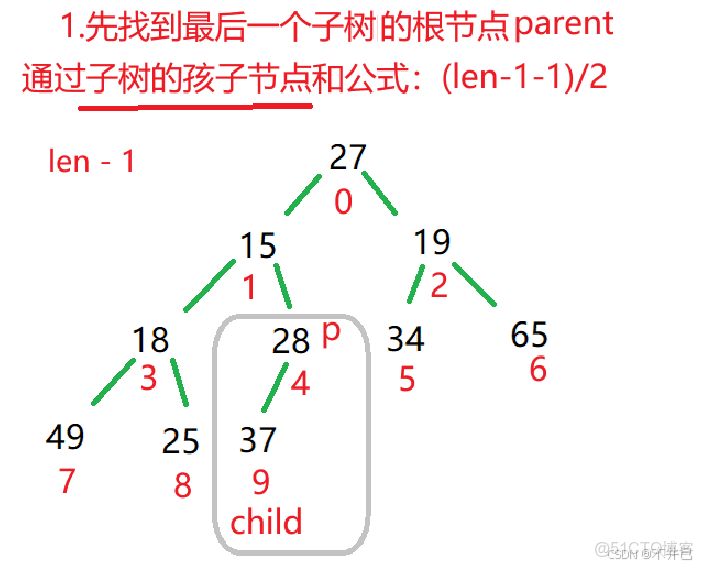
向下調整建大根堆的思路:
算法實現如下:
// 向下調整建立大根堆
public void createHeap() {
for (int parent = (this.usedSize-1-1)/2; parent >= 0; parent--) {
shiftDown(parent,this.usedSize);
}
}
// 向下調整方法
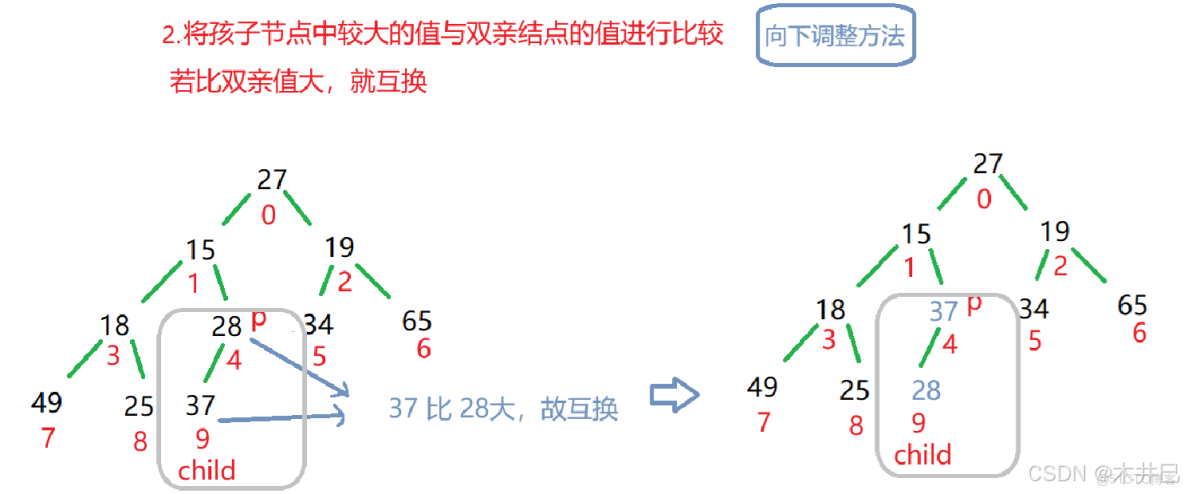
private void shiftDown(int parent, int usedSize) { //param: 起始位置和結束位置
int child = 2*parent + 1;
// 當還沒有將所有的子樹改成大根堆時
while (child < this.usedSize) {
// 找到孩子節點中的最大值
if ((child+1)<this.usedSize && elem[child]<elem[child+1]) {
child++;
}
// 將找到的最大值與雙親的值進行比較
if (elem[child] > elem[parent]) {
// 若比雙親的值大,進行交換
swap(elem,child,parent);
// 然後往子樹走
parent = child;
child = 2*parent + 1;
} else {
// 若比雙親的值小,就直接退出
break;
}
}
}向下調整方法的時間複雜度:最壞情況下,需要從根節點調整到葉子節點,調整路徑的長度為樹的高度,因此時間複雜度為 O ( logN )。
而向下調整建堆的時間複雜度是 O ( NlogN ),通常N是很小的數字,故可近似為 O ( N )。
3.2.2 向上調整(Shift Up)
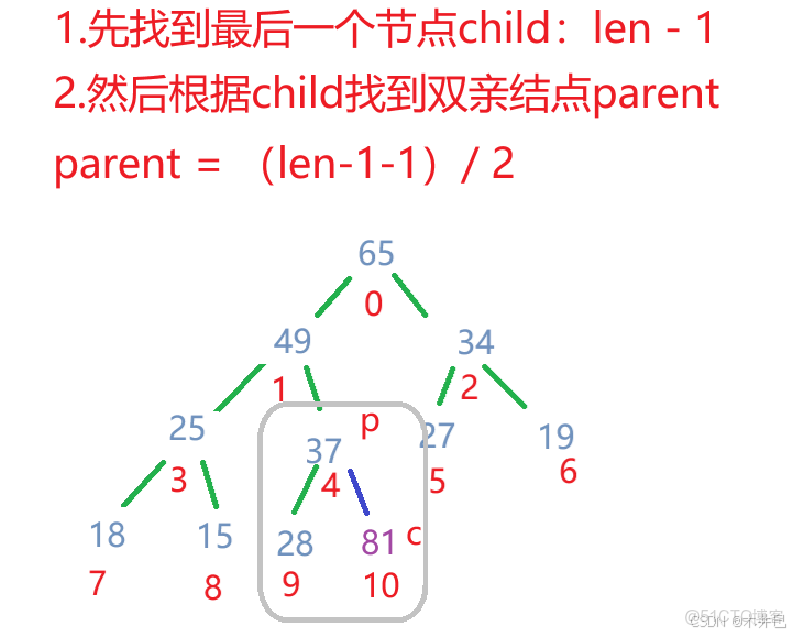
向上調整用於在堆中插入新元素時維護堆的性質。新元素通常放在堆的末尾,然後通過向上調整找到其合適位置。
向上調整方法的思路:
算法實現如下:
// 向上調整方法
private void shiftUp(int child) {
int parent = (child-1) / 2;
while (parent >= 0) {
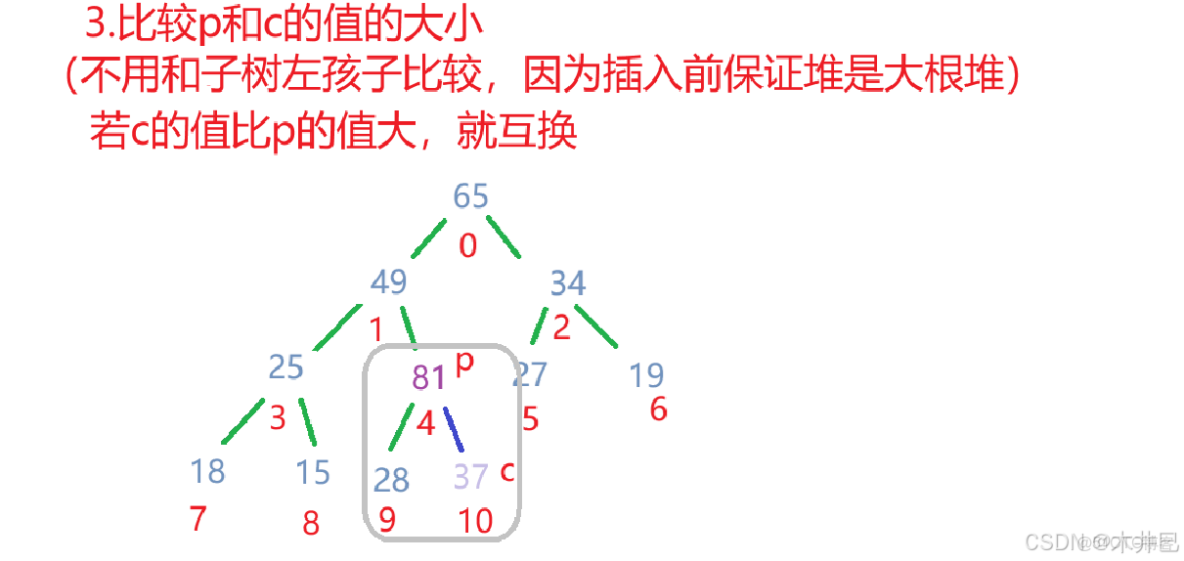
// 將新元素與雙親的值比較
if (elem[child] > elem[parent]) {
// 若比雙親的值大,進行交換
swap(elem,child,parent);
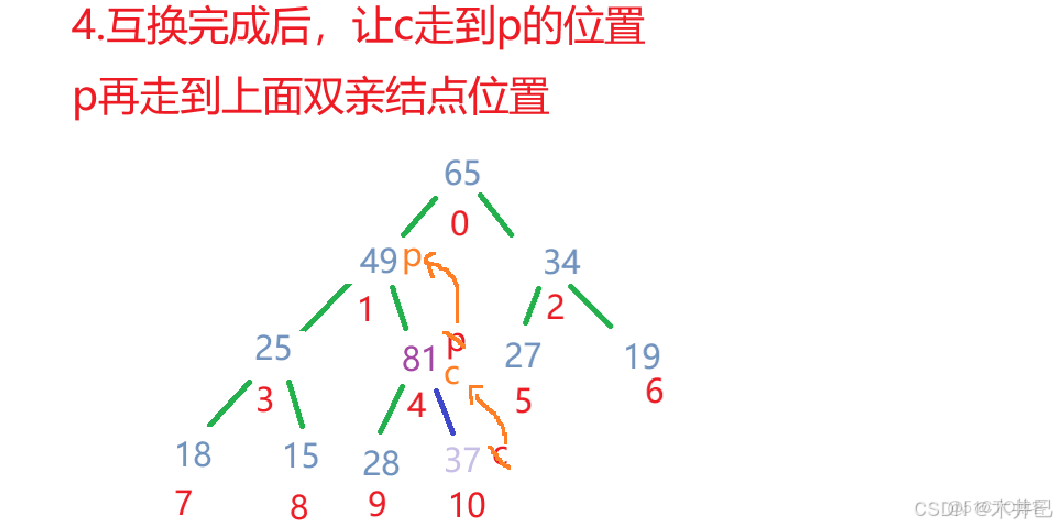
// 然後往父樹走
child = parent;
parent = (child-1) / 2;
} else {
// 若比雙親的值小,就直接退出
break;
}
}
}3.2.3 插入與刪除操作
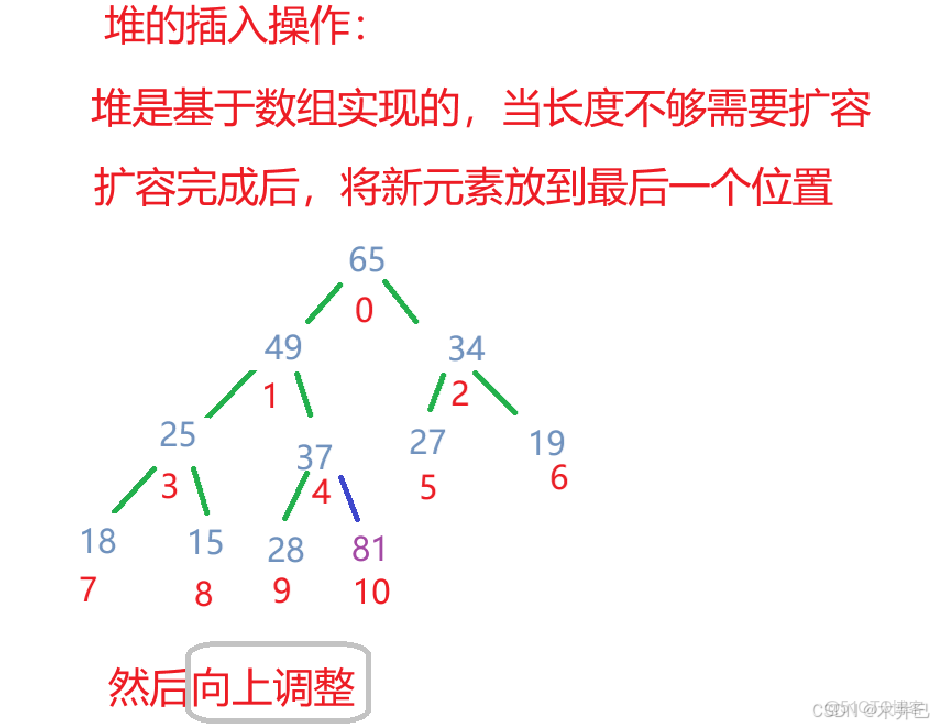
堆的插入:
- 將新元素放入堆的末尾
- 對新元素執行向上調整
算法實現如下:
// 插入操作
public void offer(int val) {
// 判斷是否已滿,若滿就擴容
if (isFull()) {
this.elem = Arrays.copyOf(this.elem,2*this.elem.length);
}
// 把新元素放入最後一個節點
elem[usedSize] = val;
// 向上擴容調整大根堆
shiftUp(usedSize++);
}
private boolean isFull() {
return this.usedSize == this.elem.length;
}
// 向上調整方法
private void shiftUp(int child) {
int parent = (child-1) / 2;
while (parent >= 0) {
// 將新元素與雙親的值比較
if (elem[child] > elem[parent]) {
// 若比雙親的值大,進行交換
swap(elem,child,parent);
// 然後往父樹走
child = parent;
parent = (child-1) / 2;
} else {
// 若比雙親的值小,就直接退出
break;
}
}
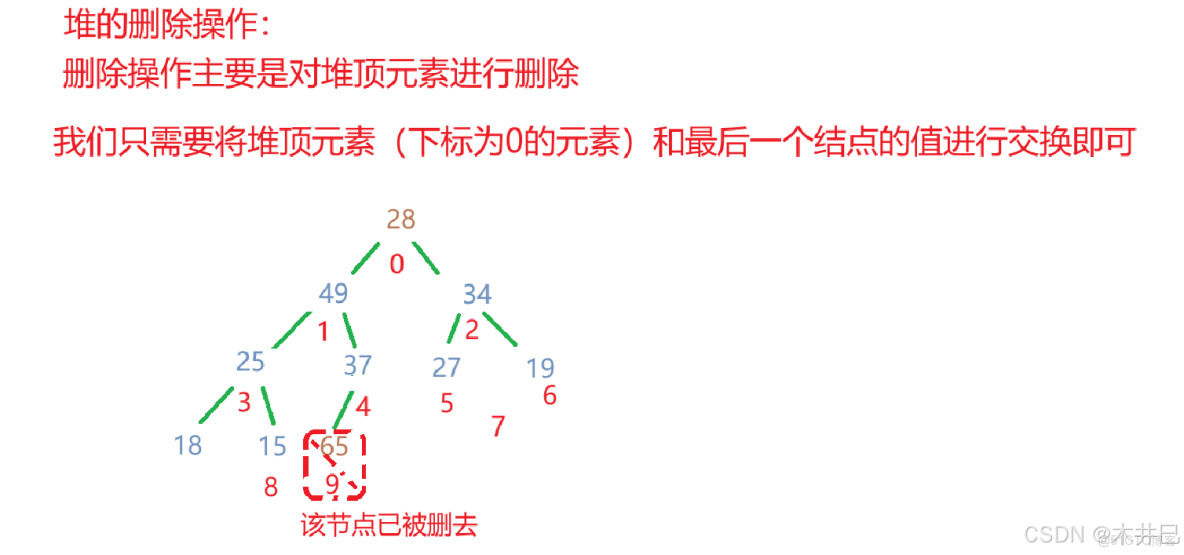
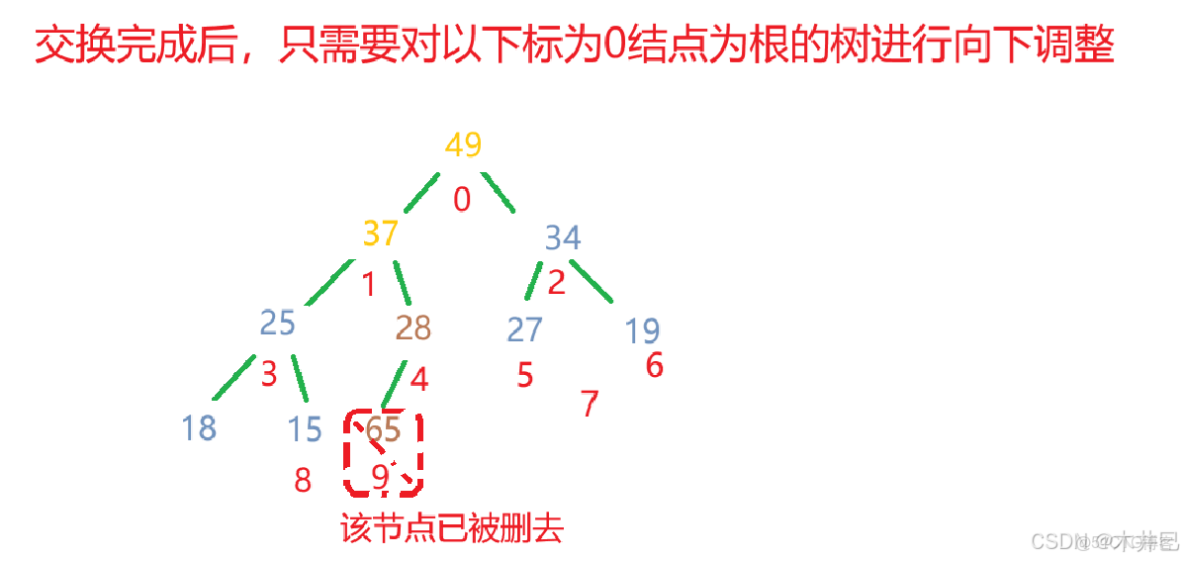
}堆的刪除:
- 將堆頂元素與最後一個元素交換
- 減少堆的大小
- 對新的堆頂元素執行向下調整
算法實現如下:
// 刪除操作
public int poll() {
// 如果堆為空,返回-1
if (isEmpty())
return -1;
int end = this.usedSize - 1;
int val = elem[0];
// 把堆頂元素和最後元素交換
swap(elem,0,end);
// 向下調整以堆頂元素為根的樹即可
shiftDown(0,end);
this.usedSize--;
return val;
}
private boolean isEmpty() {
return this.usedSize == 0;
}
public void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
// 向下調整方法
private void shiftDown(int parent, int usedSize) { //param: 起始位置和結束位置
int child = 2*parent + 1;
// 當還沒有將所有的子樹改成大根堆時
while (child < this.usedSize) {
// 找到孩子節點中的最大值
if ((child+1)<this.usedSize && elem[child]<elem[child+1]) {
child++;
}
// 將找到的最大值與雙親的值進行比較
if (elem[child] > elem[parent]) {
// 若比雙親的值大,進行交換
swap(elem,child,parent);
// 然後往子樹走
parent = child;
child = 2*parent + 1;
} else {
// 若比雙親的值小,就直接退出
break;
}
}
}四、Java中的PriorityQueue
4.1 基本特性
Java提供了 PriorityQueue類 作為優先級隊列的實現:
- 線程不安全
- 不允許null元素
- 元素必須實現Comparable接口或提供Comparator
- 默認是小根堆
4.2 構造方法
// 1. 默認構造方法(小根堆,初始容量11)
PriorityQueue<Integer> pq1 = new PriorityQueue<>();
// 2. 指定初始容量
PriorityQueue<Integer> pq2 = new PriorityQueue<>(100);
// 3. 使用集合初始化
List<Integer> list = Arrays.asList(5, 3, 8, 1, 2);
PriorityQueue<Integer> pq3 = new PriorityQueue<>(list);
// 4. 使用自定義比較器(大根堆)
PriorityQueue<Integer> maxHeap = new PriorityQueue<>((a, b) -> b - a);4.3 自定義比較器
// 大根堆比較器
class DescComparator implements Comparator<Integer> {
@Override
public int compare(Integer o1, Integer o2) {
return o2.compareTo(o1); // 降序排列
}
}
// 使用示例
PriorityQueue<Integer> maxHeap = new PriorityQueue<>(new DescComparator());4.4 擴容機制
Java的PriorityQueue有自動擴容機制:
- 當容量小於64時,按當前容量的2倍擴容
- 當容量大於等於64時,按當前容量的1.5倍擴容
- 最大容量為Integer.MAX_VALUE - 8
五、堆的實戰
5.1 堆排序
從小到大升序——>大根堆
從大到小降序——>小根堆
算法實現思路(升序,使用大根堆):
- 將堆頂元素即下標為0的元素和堆底最後一個元素end交換,交換完成後end--
- 向下調整,每一次調整end都要減一
- 堆從後往前就逐漸由大到小排序了
- 當end大於0時才進行以上操作,否則結束循環
算法實現如下:
// 堆排序
public void heapSort() {
int end = this.usedSize - 1; // end表示最後的元素
// 遍歷數據,當最後元素下標不為負數就一直排序
while (end > 0) {
// 堆頂元素和下標為end的元素進行交換
swap(elem,0,end);
// 向下調整
shiftDown(0, end--);
}
}
public void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
// 向下調整方法
private void shiftDown(int parent, int usedSize) { //param: 起始位置和結束位置
int child = 2*parent + 1;
// 當還沒有將所有的子樹改成大根堆時
while (child < this.usedSize) {
// 找到孩子節點中的最大值
if ((child+1)<this.usedSize && elem[child]<elem[child+1]) {
child++;
}
// 將找到的最大值與雙親的值進行比較
if (elem[child] > elem[parent]) {
// 若比雙親的值大,進行交換
swap(elem,child,parent);
// 然後往子樹走
parent = child;
child = 2*parent + 1;
} else {
// 若比雙親的值小,就直接退出
break;
}
}
}5.2 Top-K
返回最小的K個數
- 思路一:整體排序;
- 思路二:建立一個大小為K的小根堆;
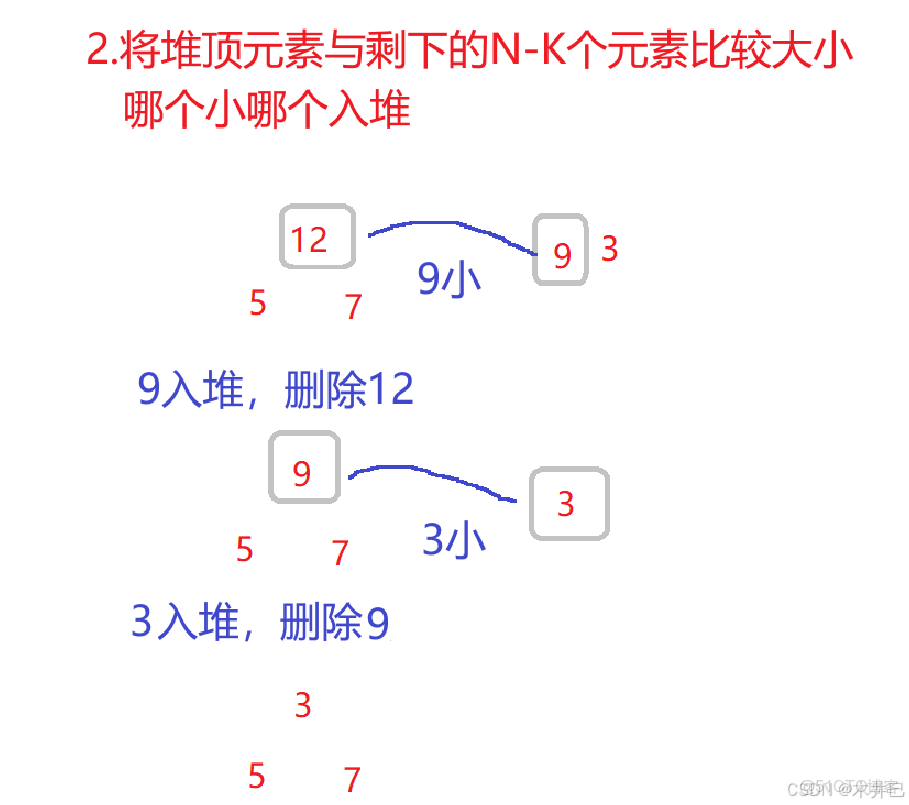
- 思路三:把前K個元素創建為大小為K的大根堆,遍歷剩下的N-K個元素並依次與堆頂元素比較大小,若比堆頂元素小就調換
我們這裏採用思路三:
假設數據是:12,5,7,9,3
要返回前3個最小的數
- 我們這裏採用Java內置的PriorityQueue,它會自動進行調整
- 在進行實例化優先級隊列的時候,我們採用自定義比較器,保證建立的是大根堆
算法實現如下:
// 自定義比較器
class Intcmp implements Comparator<Integer> {
@Override
public int compare(Integer o1, Integer o2) {
return o2.compareTo(o1);
}
}
public int[] smallestK(int[] arr, int k) {
int[] ret = new int[k];
if (arr==null || k==0)
return ret;
// 創建大小為K的大根堆
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(k,new Intcmp());
for (int i = 0; i < k; i++) {
priorityQueue.offer(arr[i]);
}
// 比較堆頂元素
for (int i = k; i < arr.length; i++) {
int val = priorityQueue.peek();
if (arr[i] < val) {
priorityQueue.poll();
priorityQueue.offer(arr[i]);
}
}
// 將大根堆存入數組
for (int i = 0; i < k; i++) {
ret[i] = priorityQueue.poll();
}
return ret;
}希望讀者看到這裏,能夠掌握以上的基本知識並熟練運用。
完